Устойчивость шарнирно опертого в плоскости и из плоскости изгиба бруса квадратного поперечного сечения под действием сосредоточенной поперечной изгибающей силы, приложенной в середине пролета в уровне продольной оси верхней грани (поперечный изгиб)

Цель: Определение критического значения сосредоточенной поперечной изгибающей силы, действующей в середине пролета в уровне продольной оси верхней грани шарнирно опертого в плоскости и из плоскости изгиба бруса квадратного поперечного сечения, соответствующего моменту потери его устойчивости.

Файлы с исходными данными:

Имя файла	Описание файла расчета
Stability_Bar_11_Bar.SPR	Стержневая расчетная модель
Stability_Bar_11_Shell.SPR	Оболочечная расчетная модель

Формулировка задачи: Шарнирно опертый в плоскости и из плоскости изгиба брус квадратного поперечного сечения подвергается воздействию сосредоточенной поперечной изгибающей силы P, действующей в середине его пролета в уровне продольной оси верхней грани. Определить критическое значение сосредоточенной поперечной изгибающей силы P, соответствующее моменту потери устойчивости шарнирно опертого бруса.  

Ссылки: Вольмир А.С., Устойчивость деформируемых систем, Москва, Наука, 1967, стр.219

Исходные данные:

L = 10.0 м	- длина шарнирно опертого бруса;
h = b = 1.0 м	- сторона квадратного поперечного сечения шарнирно опертого бруса;
E = 3.0·107 кН/м2	- модуль упругости материала шарнирно опертого бруса;
ν = 0.2	- коэффициент Пуассона;
P = 106 кН	- начальное значение сосредоточенной поперечной изгибающей силы, действующей в середине пролета в уровне продольной оси верхней грани бруса.

 

Конечноэлементная модель: Расчетная схема – система общего вида. Рассматриваются две расчетные модели:

 

Стержневая модель (С), 10 элементов типа 5, сетка конечных элементов разбита по длине продольной оси полосы с шагом 1.0 м. Обеспечение граничных условий достигается за счет наложения связей на узлы шарнирно опертых торцов бруса по направлениям степеней свободы X, Y, Z, UX. К узлу середины пролета бруса примыкает  1 двухузловой элемент типа 100 (трехмерное твердое тело), расположенный вертикально вверх с длиной, равной h/2. Воздействие с начальным значением сосредоточенной поперечной изгибающей силы P задается в в свободном узле элемента твердого тела (повышенная точка приложения). Количество узлов в расчетной схеме – 12;

Оболочечная модель теории Рейсснера-Миндлина (П), 2560 восьмиузловых элементов типа 150, сетка конечных элементов разбита по длине продольной оси и высоте бруса с шагом 0.0625 м. Опирание оболочки производится через вертикальные стержни повышенной жесткости (h = b = 1.0 м; E = 3.0·10⁹ кН/м²; ν = 0.2), 64 элемента типа 5. Обеспечение граничных условий достигается за счет наложения связей на узлы торцов бруса, находящиеся на его продольной оси, по направлениям степеней свободы X, Y, Z и на все остальные узлы торцов бруса по направлению степени свободы Y. Воздействие с начальным значением сосредоточенной поперечной изгибающей силы P задается в узле, расположенном в середине пролета бруса  и отстоящем по высоте от продольной оси бруса на h/2. Количество узлов в расчетной схеме – 8033.

Результаты решения в SCAD

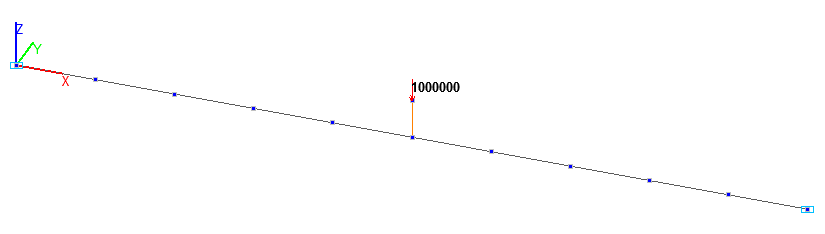
Расчетная схема. Стержневая модель

 

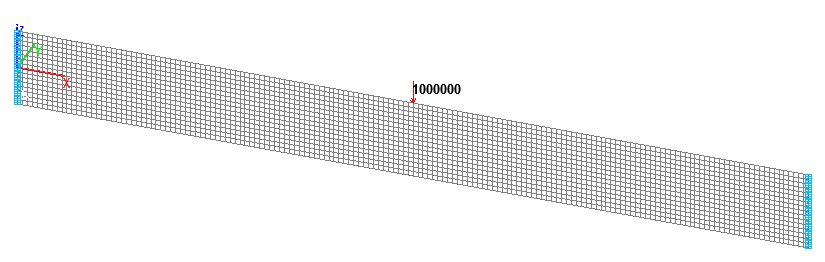
Расчетная схема. Оболочечная модель теории Рейсснера-Миндлина

 

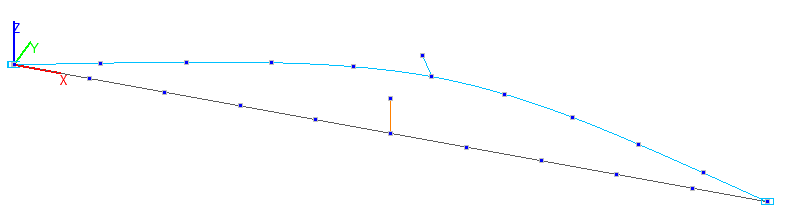
1-ая Форма потери устойчивости. Стержневая модель

 

1-ая Форма потери устойчивости. Оболочечная модель теории Рейсснера-Миндлина

Сравнение решений:

Критическое значение сосредоточенной поперечной изгибающей силы P_cr (кН), действующей в середине пролета в уровне продольной оси верхней грани шарнирно опертого в плоскости и из плоскости изгиба бруса

Расчетная модель	Теория	SCAD	Отклонение, %
Стержневая	317747	0,313904∙106=313904	1,21
Оболочечная теории Рейсснера-Миндлина	317747	0,304932∙106=304932	4,03

Замечания: При аналитическом решении критическое значение сосредоточенной поперечной изгибающей силы P_cr, соответствующее моменту потери устойчивости шарнирно опертого бруса, определяется по следующей формуле:

\[ P=\frac{16,94\cdot \sqrt {E\cdot I_{z} \cdot G\cdot I_{x} } }{L^{2}}\cdot k_{h} \quad k_{h} =f\left( {\frac{h}{2\cdot L}\cdot \sqrt {\frac{E\cdot I_{z} }{G\cdot I_{x} }} } \right) \quad G=\frac{E}{2\cdot \left( {1+\nu } \right)} \]

\( I_{z} =\frac{h\cdot b^{3}}{12} \) – наименьший момент инерции изгиба (из плоскости действия момента);

\( I_{y} =\frac{b\cdot h^{3}}{12} \) – наибольший момент инерции изгиба (в плоскости действия момента);

\( I_{x} =k_{f} \cdot h\cdot b^{3} \) – момент инерции свободного кручения, где:

\[ k_{f} =\frac{1}{3}\cdot \left\{ {1-\frac{192}{\pi^{5}}\cdot \frac{b}{h}\cdot \sum\limits_{n=1}^\infty {\left[ {\sin^{2}\left( {\frac{n\cdot \pi }{2}} \right)\cdot \frac{1}{n^{5}}\cdot th\left( {\frac{n\cdot \pi \cdot h}{2\cdot b}} \right)} \right]} } \right\} \]