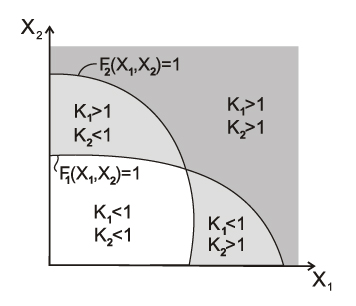
Рис. 1. Геометрическая иллюстрация формирования области несущей способности в двухмерном пространстве внутренних усилий
Программа АРБАТ предназначена для проверки несущей способности или подбора арматуры в элементах бетонных и железобетонных конструкций, для вычисления прогибов в железобетонных балках, для проверки местной прочности элементов железобетонных конструкций (включая закладные детали) согласно требованиям одного из следующих нормативных документов:
Расчет выполняется с учетом предельных состояний первой и второй группы (прочность и трещиностойкость) для расчетных сочетаний усилий (РСУ), выбираемых автоматически в зависимости от заданных расчетных нагрузок в соответствии с требованиями СНиП 2.01.07-85* "Нагрузки и воздействия" и СНиП 2.03.01-84* "Бетонные и железобетонные конструкции" (СНиП 52-01-2003). Если в качестве норм проектирования выбран СП 63.13330, то комбинирование нагрузок производится в соответствии с требованиями СП 20.13330.
Во всех режимах задаются расчетные значения нагрузок (усилий). При анализе второго предельного состояния применяются нормативные значения нагрузок. При переходе от расчетных значений к нормативным для каждого загружения используются коэффициенты надежности по нагрузке, задаваемые пользователем.
Подбор арматуры и проверка выполняются для балок, колонн и плит из тяжелого, мелкозернистого и легкого бетонов с применением арматурной стали классов А-I (A240), A-II (A300), A-III (A400), A-IV, A-V и A-VI, а также арматурной проволоки класса Вp-I (B500) и арматуры классов А400С, А500С (A500), А600С. Кроме того, подбор и проверка реализованы для композитной арматуры АСК, АБК, АУК, ААК, АКК в соответствии с требованиями СП 295.1325800.
Кроме того, программа АРБАТ выполняет роль справочника, с помощью которого можно получить данные о сортаментах и характеристиках арматуры, нормативных и расчетных сопротивлениях бетона, коэффициентах условий работы бетона и допускаемых предельных прогибах.
Реализованные в программе принципы управления, подготовки данных и документирования результатов расчета полностью совпадают с аналогичными режимами проектно-аналитических программ, входящих в состав системы SCAD Office®. Программы используют известную технику работы с многостраничными окнами. Активизация страницы происходит при нажатии на ее закладку, кроме того, используются меню.
Нормы проектирования строительных конструкций построены как система проверок известного конструктивного решения, т.е. они решают задачу оценки конструкций, а не проблему ее синтеза. Программа АРБАТ нацелена на решение обеих упомянутых проблем – задачи оценки и задачи подбора. Но последняя проблема (подбор) решается в ограниченной постановке как целенаправленный перебор по списку возможных конструктивных решений.
Так, например, при проектировании стальных конструкций в программе Кристалл подбираются сечения из указанного сортамента профилей и производится выбор сечения с наименьшим расходом стали.
Описанный подход к подбору (синтезу) поперечного сечения приводит к решениям, которые по той или иной причине (конструктивным соображениям, унификации и др.) могут не удовлетворить проектировщика. Он имеет возможность скорректировать решение, предлагаемое программой, и оперативно провести его проверку в режиме экспертизы.
Нормативные требования (условия прочности, общей и местной устойчивости, предельной гибкости и т.п.), предъявляемые к некоторому элементу конструкции, можно записать в виде некоторого набора ограничений-неравенств, каждое из которых функционально зависит от значений внутренних усилий \( \vec{{S}} = \{ S_{1}, S_{2}, ... , S_{n} \} \), которые могут возникать в рассматриваемом сечении от действия комбинаций нагружений:
\[ {\rm {\bf \Phi }}\left( {\vec{{S}},\vec{{R}}} \right)\le 1 ;\]
или
\[ \left\{ {{\begin{array}{*{20}c} {f_{1} \left( {\vec{{S}},\vec{{R}}} \right)\le 1;} \\ {f_{2} \left( {\vec{{S}},\vec{{R}}} \right)\le 1;} \\ {...} \\ {f_{j} \left( {\vec{{S}},\vec{{R}}} \right)\le 1;} \\ {...} \\ {f_{m} \left( {\vec{{S}},\vec{{R}}} \right)\le 1;} \\ \end{array} }} \right. ,\]
где n – общее количество возможных внутренних усилий; m – количество неравенств, описывающих требования норм проектирования; fi – функция основных переменных, реализующая j-ю проверку; \( \vec{{R}} \) – обобщенные сопротивления.
Ориентируясь на значения функций \( K_{j} =f_{j} \left( {\vec{{S}},\vec{{R}}} \right) \), можно ввести понятие коэффициента использования ограничения, и приведенный критерий обеспечения несущей способности элемента конструкции представить в виде:
\[ K_{\max } =\max \left\{ {K_{j} \quad \vert \quad j=1,...,m} \right\}\le 1 , \]
где \(К_j\) – левая часть расчетного неравенства \[ f_{j} \left( {\vec{{S}},\vec{{R}}} \right)\le 1 \]
включающего нормативные проверки. Само значение Кj при этом определяет для элемента конструкции (сечения, соединения, узла и т.п.) имеющийся запас прочности, устойчивости или другого нормируемого параметра обеспечения несущей способности. Если требование норм выполняется с запасом, то коэффициент Кj равен относительной величине исчерпания нормативного требования (например, Кj = 0,7 соответствует 30%-му запасу). При невыполнении требований норм значение Кj > 1 свидетельствует о нарушении того или иного требования, т.е. характеризует степень перегрузки.
Каждое нормативное требование \[ K_{\max } =\max \left\{ {K_{j} \quad \vert \quad j=1,...,m} \right\}\le 1 \] определяет некоторую область Ωj в n-мерном пространстве внутренних усилий, а пересечение всех областей Ωj образует область несущей способности элемента конструкции Ω в терминах рассматриваемых норм проектирования (рис. 1). Для каждой точки области несущей способности максимальный коэффициент использования ограничений \( K_{\max } =\max \left\{ {K_{j} \quad \vert \quad j=1,...,m} \right\}\le 1 \).
Рис. 1. Геометрическая иллюстрация формирования
области несущей способности в двухмерном пространстве внутренних усилий
Как правило, нормативные ограничения записывают как:
\[ \varphi_{j} \left( {\vec{{S}}} \right)\le \psi_{j} \left( {\vec{{R}}} \right), (j = 1, …,m), \]
где φj, ψj – функции основных переменных, реализующие j-ю проверку.
Однако не всегда эти требования можно или нужно переписать в виде:
\[ f_{j} \left( {\vec{{S}},\vec{{R}}} \right)\le 1, (j = 1,…, m), \text {где} \] \[ f_{j} \left( {\vec{{S}},\vec{{R}}} \right)=\frac{\varphi_{j} (\vec{{S}})}{\psi_{j} (\vec{{R}})}, \]
то есть в виде отношения левой части нормативного неравенства к его правой части.
Чтобы проиллюстрировать сказанное рассмотрим в качестве примера формулу (8.78) СП 63.13330:
\[ T\le T_{0} \sqrt {1-\left( {\frac{M}{M_{0} }} \right)^{2}}. \]
Если бы в качестве значения коэффициента использования данной нормативной проверки вычислялось отношение:
\[ \frac{T}{T_{0} \sqrt {1-\left( {\frac{M}{M_{0} }} \right)^{2}} }\le 1, \]
то в расчетной ситуации, когда M < M0, мы в знаменателе получали бы корень из отрицательного числа и не смогли бы получить количественную оценку превышения несущей способности, чего удается избежать преобразовав формулу (8.78) следующим образом:
\[ \left( {\frac{T}{T_{0} }} \right)^{2}+\left( {\frac{M}{M_{0} }} \right)^{2}\le 1. \]
Другим примером может служить формула (8.10) СП 63.13330
\[ Ne\leq R_b b x(h_0-x/2)+R_{sc} A_s^\prime(h_0-a^\prime), \]
для которой так же нельзя в качестве фактора использовать отношение левой и правой частей, поскольку высота сжатой зоны x зависит от продольной силы.
Численное значение фактора (значение коэффициента использования нормативного ограничения) является мерой того, на сколько полно использована (или превышена) несущая способность элемента конструкции, и, как следствие, позволяет проектировщику принять правильное решение о типе необходимой модификации конструкции и только! К примеру, вряд ли имеет смысл принимать другую марку стали с большим расчетным сопротивлением в том случае, когда критической оказалась проверка устойчивости.
Необходимо особо подчеркнуть, что может не существовать прямой пропорциональности между значением фактора и значениями усилий, фигурирующих в нормативной проверке, как и может не существовать прямой пропорциональности между значением фактора и значениями геометрических характеристик сечений элементов конструкций. Это обусловлено нелинейностью нормативных проверок, в частности, нелинейностью функции коэффициента продольного изгиба и т.д.
Все полученные в результате проверок значения коэффициентов Кj доступны для анализа в диалоговом окне Диаграмма факторов или же в полном отчете о проведенной проверке. В рабочих диалоговых окнах выводится значение Кmax – максимального (т.е. наиболее опасного) из обнаруженных значений Кj и указывается тип проверки (например, прочность, устойчивость), при которой этот максимум реализовался.
Данные, приведенные в диаграмме факторов, позволяют проектировщику принять правильное решение о типе необходимой модификации конструкции. Например, вряд ли имеет смысл увеличение расчетного сопротивления стали, если критической оказалась проверка устойчивости.
Для стержневых элементов строительных конструкций, в сечениях которых под нагрузкой могут возникать шесть внутренних усилий (продольная сила, изгибающие моменты, поперечные силы, а также крутящий момент), область несущей способности представляет собой шестимерный геометрический объект, который трудно анализировать. Наиболее наглядно отобразить область несущей способности сечений можно с помощью ее ортогонального проецирования на некоторую плоскость (пару) внутренних усилий. Автоматизированное построение двумерной проекции области несущей способности сечения выполняется следующим образом.
Пользователем выбирается пара внутренних усилий (например, пара «продольная сила N – изгибающий момент My»), в системе координат которой будет построена ортогональная проекция области несущей способности. Остальные внутренние усилия в сечении (Mz, Qy, Qz, Mx) фиксируются на некотором уровне (задаются пользователем или принимают нулевые значения). При некотором фиксированном значении отношения e = My/N разыскивается ближайшая к началу координат точка, где некоторое неравенство из набора \( {\rm {\bf \Phi }}\left( {\vec{{S}},\vec{{R}}} \right)\le 1 \) принимает предельное значение \( f_{j} \left( {\vec{{S}},\vec{{R}}} \right)=1 \). Такая точка принадлежит границе двумерной ортогональной проекции области несущей способности сечения.
Представленный способ автоматизированного построения области несущей способности предполагает, что область обладает свойством звездности, что является гипотезой, с одной стороны, и ограничением программной реализации, с другой стороны.
Кроме того, построенная область является интерактивным инструментом общения с пользователем. С помощью курсора мыши можно исследовать двухмерную проекцию области. Каждому положению курсора соответствует определенный набор внутренних усилий, значения которых отображаются в соответствующих полях. В зависимости от изменения положения курсора (изменения значений для соответствующей пары внутренних усилий) выводится максимальное значение коэффициента использования нормативных ограничений-неравенств Кmax, соответствующее этим усилиям, а также тип нормативного неравенства, для которого он вычислен. Нажатие правой кнопки мыши позволяет увидеть весь список выполненных проверок и значений коэффициентов использования ограничений \( K_{j} (j=\overline {1,m} ) \) для того набора внутренних усилий, который соответствует положению курсора. Кроме того, программа обеспечивает также следующие операции с мышью:
Одним из важнейших свойств области несущей способности является выпуклость. Заметим, что именно выпуклость области несущей способности сечения дает нам право в линейном расчете ограничиться проверками такого сечения на действие только тех сочетаний внутренних усилий в сечении, для которых характерны экстремальные (минимальные или максимальные) значения. Положительный результат таких проверок автоматически означает, что и все другие мыслимые комбинации нагрузок окажутся допустимыми.
Отсутствие свойства выпуклости области несущей способности для рассматриваемого сечения может привести ко многим неприятным последствиям, связанным с тем обстоятельством, что по традиции оценивая невыгодные сочетания внутренних усилий, инженеры либо вообще не рассматривают некоторые воздействия (в том случае, когда они оказывают разгружающее действие), либо учитывают их полностью. Это правило целиком справедливо для выпуклой области несущей способности, в то время, как для невыпуклой области невыгодным может оказаться сочетание с промежуточными (не экстремальными) значениями внутренних усилий.
При автоматизированном построении области несущей способности сечения выполняется несколько тысяч расчетов, что является, по-видимому, наиболее массовой проверкой рассматриваемого сечения. Кроме того, форма области несущей способности сечения, а также характер ее границ позволяет во многих случаях более детально проанализировать требования норм проектирования, нежели это удается сделать другими способами. Анализ формы области позволяет выполнить проверку непротиворечивости, согласованности и полноты нормативных требований. При этом легко выявляются противоречивость отдельных положений нормативного документа, а также их нестыковки, в частности негладкость сопряжения используемых аппроксимаций.
СП63.13330 Железобетонные конструкции
В качестве примера рассмотрим нормы проектирования железобетонных конструкций. Рассмотрим прямоугольное железобетонное сечение с размерами 700мм × 200мм, армированное 2 стержнями арматуры диаметром 28 мм. Области несущей способности такого сечения, соответствующие двум вариантам нормативных требований по обеспечению трещиностойкости, приведены на рис. 2 в осях «продольная сила N – изгибающий момент Мy». Область Ω1 построена с учетом нормативного ограничения ширины раскрытия трещин, а область Ω2 – с учетом запрета трещинообразования. При этом следует отметить, что обе методики нормативной проверки железобетонных сечений на трещиностойкость являются полуэмпирическими. Рассмотрим, с чем связана невыпуклость области несущей способности железобетонного сечения.
Скачок АВ, который характерен для обеих областей несущей способности Ω1 и Ω2, определяется постулатом теории железобетона, предусматривающим мгновенное исключение из работы растянутой зоны бетона при появлении растягивающих напряжений в нем.
Скачок ВС характерен только для области несущей способности железобетонного сечения Ω2, построенной с учетом запрета трещинообразования. В данном случае область Ω2 резко сужается, что является вполне ожидаемым и, кроме того, приобретает весьма изощренную форму, обусловленную новой методикой проверки железобетонных элементов на трещиностойкость, которая появилась в редакции норм 2004 года.
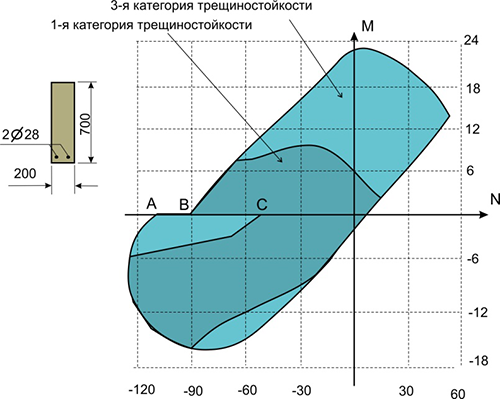
Рис. 2. Области несущей
способности железобетонного сечения по СП 63.13330:
Ω1 – при ограничении ширины
раскрытия трещин (3-я категория трещиностойкости);
Ω2 – при запрете образования
трещин (1-я категория трещиностойкости)
Другой поучительный пример представлен на рис. 3, где показана область несущей способности железобетонного сечения, рассчитанного по нелинейной деформационной модели без учета (вариант а) и с учетом (вариант b) случайного эксцентриситета. Очевидна «нефизичность» учета этого эксцентриситета в варианте, представленном в нормах проектирования, поскольку нет никакой физической модели нарушающей гладкость границы области несущей способности. Указание норм таково, что для статически неопределимой системы значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения e0 принимают равным значению эксцентриситета е, полученного из статического расчета, но не менее некоторой фиксированной величины случайного эксцентриситета ea, а для статически определимой системы эксцентриситет e0 принимают равным величине e + ea. В обоих случаях при малых значениях эксцентриситета е рассматривается внецентренно сжатый элемент, при этом эксцентриситет e0 не бывает малым.
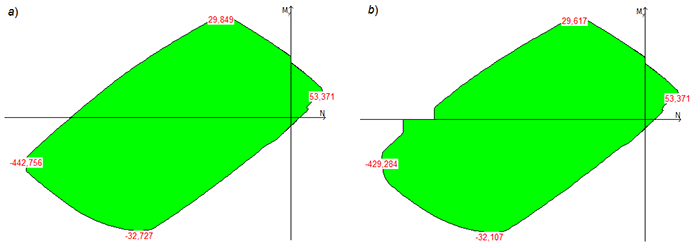
Рис. 3. Влияние случайного эксцентриситета на форму проекции области несущей способности железобетонного сечения
Число примеров можно было бы увеличить, но и приведенные свидетельствуют о вполне реальной ситуации, когда область несущей способности сечений может оказаться невыпуклой. Как показывает анализ, во многих случаях здесь сказываются нестыковки в части формулирования требований к стержневым элементам несущих конструкций, обусловленные, скорее всего, недостаточной отладкой самих формулировок.
Происхождение таких нестыковок связано с тем, что традиционный подход к нормированию, ориентированный на ручной счет, породил всякого рода «упрощения», при которых некоторые проверки допускалось не выполнять или подменять общий случай некоторым частным случаем.
Кроме того, использование «логических переключателей», которые меняют правила по признаку, не имеющему точной физической подосновы, приводит к скачкообразному изменению алгоритма, как при классификации поперечных сечений в Еврокоде. Современные возможности, представляемые компьютерной проверкой, позволяют выявить такие неточности и определяют пути совершенствования норм.
Опасности, связанные с невыпуклостью области несущей способности элементов конструкций, указывают на необходимость анализа близости совокупности заданных сочетаний усилий к тому участку границы области несущей способности, где проявляется свойство невыпуклости.
Практически такой анализ может быть реализован с использованием дополнительного
инструментария, представляемого компонентами SCAD
Office. Для анализа проблем, связанных с невыпуклостью области
несущей способности, предусмотрены кнопки: 
, которые позволяют
выполнить следующие действия:
– если пользователем
заданы усилия, то нажатие этой кнопки приведет к отрисовке всего множества
заданных сочетаний усилий в виде точек, каждая из которых соответствует
проекции одного из вариантов сочетаний усилий на плоскость выбранной пары
усилий (рис. 4).
– отрисовка
выпуклой оболочки указанных выше точек, т.е. всего множества точек, которые
могут быть результатом линейной комбинации заданных усилий, в том числе
и их неполных значений.
Несмотря на то, что эти комбинации не подвергались прямой проверке, в том случае, когда выпуклая оболочка нагружений не выходит из области несущей способности сечения, можно гарантировать, что и разнообразные нагружения, скомбинированные из заданных, не являются опасными.
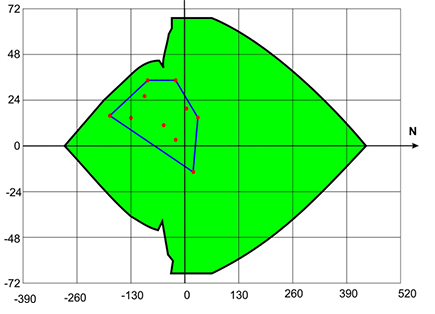
Рис. 4. Заданные (базовые) нагружения и их выпуклая оболочка, совмещенная с областью несущей способности сечения
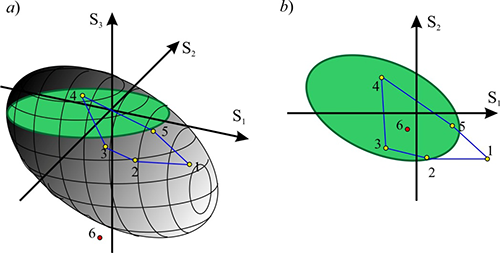
Рис. 5. Иллюстрация возможных расчетных ситуаций
Следует отметить, что представленный механизм является мощным инструментом анализа условий нагружений, но пользоваться им следует аккуратно.
Напомним, что область несущей способности сечения является телом в шестимерном пространстве внутренних усилий (с координатами N, My, Qz, Mz, Qy, T). Область несущей способности – это сечение данного тела плоскостью, а точка соответствущая набору усилий – проекция на эту плоскость. Если точка, которая соответствует некоторому набору усилий, лежит внутри области несущей способности, то отсюда еще не следует, что выполнены все требования норм. Это связано, например, с тем, что при построении области несущей способноти (кривых взаимодействия) игнорируются ограничения предельной гибкости (ведь эти ограничения не зависят от усилий) и возможна ситуация, при которой точка принадлежит области несущей способности сечения (лежит в "зеленой зоне"), но расчет покажет Kmax > 1.
Оперируя только с двухмерными ортогональными проекциями области несущей способности можно «увидеть» как проекции некоторых точек (сочетаний внутренних усилий), принадлежащих этой области (для которых максимальный коэффициент использования ограничений не превышает единицы Kmax < 1), отображаются вне границы проекции области несущей способности (как, например, точка 1 на рис. 5). Такое может произойти и в том случае, когда для заданного набора сочетаний внутренних усилий был выставлен признак "сейсмика", и, как следствие, при расчете использовался коэффициент условий работы mкр > 1. А автоматизированное построение области несущей способности (кривых взаимодействия) производится без учета коэффициента mкр. Более сложная ситуация может возникнуть при анализе кривых взаимодействия для железобетонных конструкций, поскольку у различных наборов усилий (точек) могут быть разные коэффициенты длительности.
Возможно ошибочное «видение» и обратного рода, когда проекция точки лежит в границах проекции области несущей способности, а сама точка не принадлежит области (см., например точка 6 на рис. 5).
Для идентификации описанных ситуаций, проекции точек, в которых коэффициент использования ограничений превышает единицу, отображаются на проекциях области несущей способности окрашенными в красный цвет, в противном случае — в зеленый.
В программе на страницах Кривые взаимодействия
есть кнопка 
, которая позволяет для выбранной пользователем
тройки внутренних усилий (например, My-Mz-N)
построить в трехмерном пространстве поверхность, на которой Kmax=1.
Нажатие этой кнопки приводит к появлению диалогового окна, в котором можно
выбрать какое усилие соответствует той или иной координатной оси (XYZ).
После этого кнопка Применить инициирует расчет, который можно прервать нажатием кнопки Отмена. По завершении расчета появится изображение поверхности взаимодействия.
В этом состоянии можно используя расположенные в левой части окна элементы управления
Для смены цвета или фонта следует сделать двойной щелчок мыши на соответствующей ячейке и выбрать нужные параметры.
Маркер Каркасная модель позволяет получить изображение поверхности в виде каркаса.
Нажатие правой кнопки мыши приводит к появлению контекстного меню, в котором можно выбрать нужную проекцию.
Программа обеспечивает также следующие операции с мышью:
для перехода в
режим вращения).