Назначение

Многие конструктивные элементы содержат некоторые геометрические особенности (сингулярности), например, отверстия, надрезы, и т.п.. Максимальные локальные напряжения обычно возникают именно на границе этих особенностей. Это максимальное местное напряжение σ_max намного превышает номинальное напряжение σ_nom. Отношение максимального напряжения σ_max к номинальному σ_nom называется коэффициентом концентрации напряжений K_t, то есть

\[ \sigma_{\max } =K_{\mbox{t}} \sigma_{\mbox{nom}} \]

Если рассматривается, например, плоская задача теории упругости, то в зависимости от того, как вычисляется номинальное напряжение σ_nom — на основе общей площади элемента (без вычета площади сингулярного объекта (отверстия)) или с учетом этой площади — различают коэффициент концентрации напряжений по площади брутто (K_tg) и коэффициент концентрации напряжений по площади нетто (K_tn).

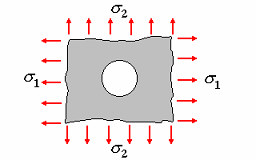
В некоторых случаях, например, если речь идет об отверстиях в бесконечных пластинах (см. рис. 1), то понятия коэффициентов концентрации напряжений по площади брутто/нетто теряют смысл, и следует говорить лишь о коэффициенте концентрации напряжений K_t.

Рис. 1. Отверстие в неограниченной пластине

Изучение концентрации напряжений основано на теоретических вычислениях, численном анализе или экспериментальных данных (фотоупругость). Многочисленные исследования концентрации напряжений были систематизированы и изложены в книге W.D.Pilkey Peterson’s Stress Concentration Factors. Реализация программы КоКон основана, в основном, на этой публикации.

В программе КоКон рассмотрено достаточно много конструктивных элементов с особенностями под действием (как правило) одной нагрузки. На практике конструктивные элементы находятся под действием комбинированных нагрузок. Чтобы оценить максимальные напряжения в этом случае достаточно, используя коэффициенты концентрации напряжений для одиночных нагрузок и номинальные напряжения, определить максимальные напряжения и использовать принцип суперпозиции (это возможно, поскольку мы предполагаем линейную работу материала конструкции и, кроме того, максимальные напряжения возникают, как правило, в одних и тех же точках при различных видах нагружения).

Кроме того, в программе КоКон реализованы режимы расчета коэффициентов интенсивности напряжений в вершине трещины. В зависимости от рассматриваемой задачи вычисляются коэффициенты интенсивности трех видов:

KI — коэффициенты интенсивности для трещин I вида (трещины отрыва или нормального отрыва);

KII, — для трещин II вида (трещины поперечного сдвига);

KIII — для трещин III вида (трещины продольного или антиплоского сдвига).

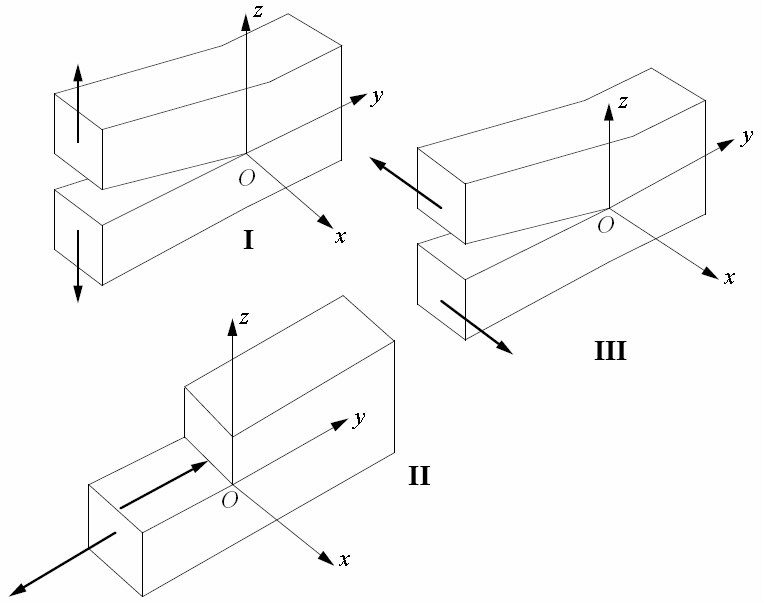
Рис 2. Три вида трещин:

I – трещины нормального отрыва, II – поперечного сдвига, III – продольного сдвига.