При использовании СНиП расчет внецентренно сжатых элементов каменных конструкций выполняется по формуле (7.4) из СП 15.13330.2020, в которую входит значение эксцентриситета e0 расчетной силы N относительно центра тяжести сечения. Этот эксцентриситет определяется эпюрой моментов, которые возникают в элементе кладки от действия сосредоточенного момента М, приложенного в верхнем сечении.
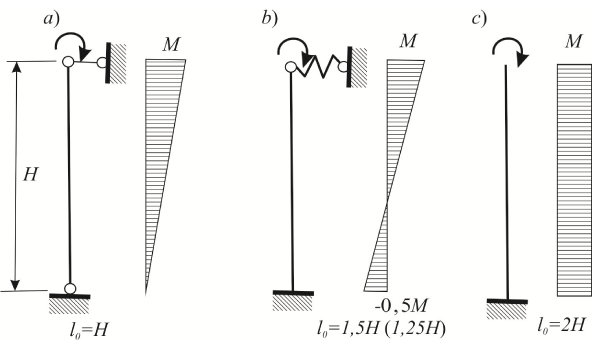
Программа предусматривает четыре варианта расчетной схемы (рис. 1) и для каждого из них следует знать расчетную высоту стены или столба l0 (коэффициент расчетной длины μ) и эпюру моментов.
В трех случаях расчетная схема указана явно и эпюра моментов определяется элементарно, соответствующие решения представлены на рис. 2.

Рис. 1
В случае «b» коэффициент расчетной длины принимается равным μ=1,5 для однопролетных зданий и μ=1,25 для многопролетных зданий.
Если же выбран вариант «Другой» и пользователь задал некоторое значение μ коэффициента свободной длины, то степень защемления в опорных сечениях необходимо согласовать с указанным значенитем μ. Для того, чтобы сделать это рассмотрим расчетную схему стержня, концы которого упруго защемлены пружинами с жесткостью k (рис.2,а). Коэффициент расчетной длины такого стержня определяется формулой (см. СП 16.13330.2011, стр. 146 или ДБН В.2.6-163: 2000, стр. 182):
\[ \mu =0,5\sqrt {\frac{\left( {\alpha +4,8} \right)\left( {\alpha +4,8} \right)}{\left( {\alpha +2,4} \right)\left( {\alpha +2,4} \right)}} ,\quad \alpha =\frac{kH}{EJ}. \]
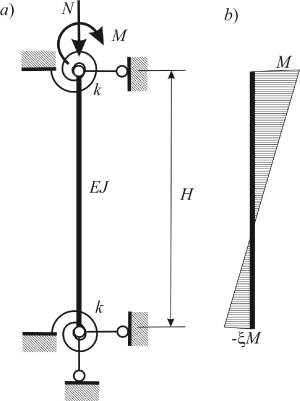
Рис. 2
Следовательно, если задана величина коэффициента μ, то жесткость защемления k определится как:
\[ \begin{array}{l} 2\mu =\frac{\left( {\alpha +4,8} \right)}{\left( {\alpha +2,4} \right)};\quad 2\mu \alpha +4,8\mu =\alpha +4,8; \\ \alpha =\frac{4,8\left( {1-\mu } \right)}{2\mu -1};\quad k=\alpha \left( {{EJ} \mathord{\left/ {\vphantom {{EJ} H}} \right. -} H} \right)=\frac{4,8EJ\left( {1-\mu } \right)}{H\left( {2\mu -1} \right)}. \\ \end{array} \]
Для такого стержня эпюра моментов характеризуется коэффициентом ξ (см. рис. 2.b) который определяется по формуле:
\[ \xi =\frac{2EJ/H}{k+4EJ/H}=\frac{2}{\alpha +4}=\frac{\left( {2\mu -1} \right)}{2,4\left( {1-\mu } \right)+2\left( {2\mu -1} \right)}=\frac{2\mu -1}{1,6\mu +0,4}. \]