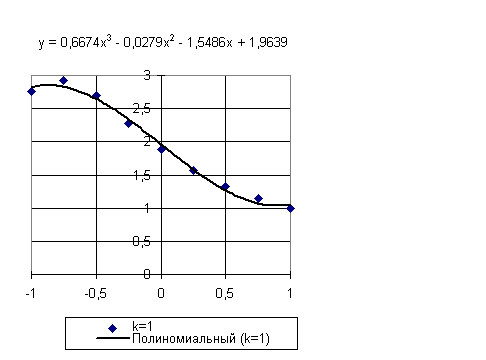
Рис.1
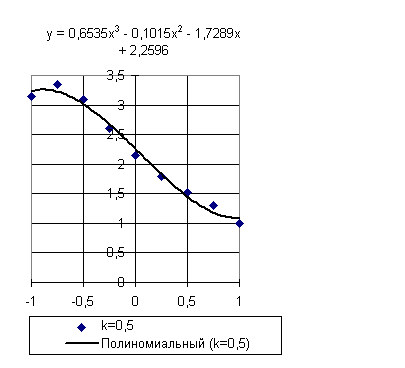
Рис.2
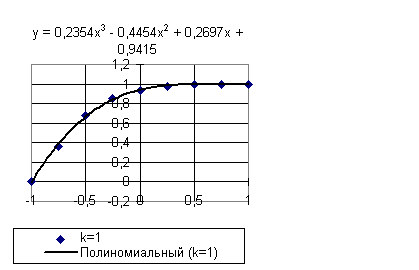
Рис.3
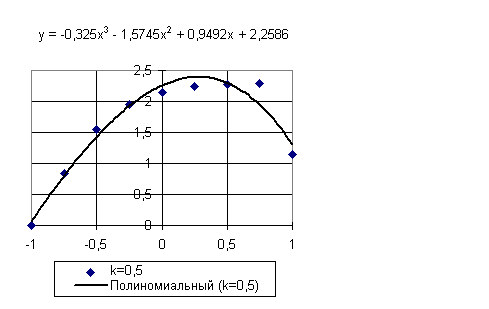
Рис.4
Вопросу определения критического момента посвящено специальное приложение NAD Франции к EN 1993-1-1. В нем для балок со сплошным поперечным сечением приводится формула для определения упругого критического момента, вызывающего изгибно-крутильное выпучивание
\[ M_{cr} =C_{1} \frac{\pi^{2}EI_{z} }{\left( {kL} \right)^{2}}\left\{ {\left[ {\left( {\frac{k}{k_{w} }} \right)^{2}\frac{I_{w} }{I_{z} }+\frac{\left( {kL} \right)^{2}GI_{t} }{\pi^{2}EI_{z} }+\left( {C_{2} z_{g} -C_{3} z_{j} } \right)^{2}} \right]^{1/2}-\left( {C_{2} z_{g} -C_{3} z_{j} } \right)}, \right\} \]
где С1, С2 и С3 это коэффициенты, значения которых зависят от вида загружения и условий опирания балки. Они представлены в таблицах F.1.1 и F.1.2 для шести базовых случаев, определяемых видом эпюры моментов.
При коэффициенте свободной длины k = 1,0 и прямолинейной эпюре моментов с концевыми значениями M и ψM указанное приложение кроме табличных значений С1 дает формулу
\[ C_{1} =1,88-1,40\psi +0,52\psi^{2} \]
Для других значений k и для других коэффициентов аналогичные формулы получены нами как аппроксимация, минимизирующая в классе полиномов третьего порядка среднеквадратичное уклонение от табличных значений. Вычисления проводились с помощью MS Excel и дали следующий результат:
Для k = 1,0: С1 = 0,6674ψ3 - 0,0279ψ2 - 1,5486ψ + 1,9639
Для k = 0,7: С1 = 0,6569ψ3 - 0,0856ψ2 - 1,6902ψ + 2,1959
Для k = 0,5: С1 = 0,6535ψ3 - 0,1015ψ2 - 1,7289ψ + 2,2596
Для k = 1,0: С3 = 0,2354ψ3 - 0,4454ψ2 + 0,2697ψ + 0,9415
Для k = 0,7: С3 = 0,0247ψ3 - 0,9187ψ2 + 0,556ψ + 1,5173
Для k = 0,5: С3 = -0,325ψ3 - 1,5745ψ2 + 0,9492ψ + 2,2586
Качество приближения видно из графиков, представленных на рисунках 1 — 4.
Следует отметить, что это еще не решает проблему, поскольку неясно, как следует поступать в случаях, когда коэффициент k имеет другое значение, и в случаях, когда эпюра моментов отлична от представленного в EN 1993-1-1 варианта.
Первая проблема решается путем интерполяции между решениями для случая k = 0,5 и случая k = 1,0.
Рис.1 |
Рис.2 |
Рис.3 |
Рис.4 |
Вторая проблема решается путем разложения фактической эпюры моментов по системе базисных эпюр, решения для которых дает приложение F.
|
M1(x) = M1f1(x) = M1(1 - x/L) M2(x) = M2f2(x) = M2x/L |
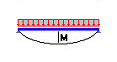 |
M3(x) = M3f3(x) = M34x(L - x)/L2 |
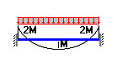 |
M4(x) = M4 f4(x) = M4[-2 + 12x(L - x)/L2] |
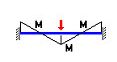 |
M5(x) = M5 f5(x) = M5(-1 + 4x/L) при (x < L/2) M5 f5(x) = M5(3 - 4x/L) при (x > L/2) |
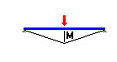 |
M6(x) = M6 f6(x) = M62x/L при (x < L/2) = M6 f6(x) = M62(1 - x/L) при (x > L/2) |
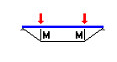 |
M7(x) = M7 f7(x) = M74x/L при (x < L/4) = M7 f7(x) = M7 при (L/4 < x < 3L/4) = M7 f7(x) = M7(4 - 4x/L) при (x > 3L/4) |
Разложение по этой системе функций реализуется путем подбора коэффициентов Xi, с помощью которых минимизируется функционал среднеквадратичного уклонения заданной эпюры M(x) от взвешенной суммы базисных эпюр
\[ D=\int\limits_0^L {\left[ {M(x)-\sum\limits_{i=1}^7 {X_{i} f_{i} (x)} } \right]}^{2}dx. \]
Определение средневзвешенных значений коэффициентов:
ψ = X1/X2;
{C1 = X1(1,9639 - 1,548ψ - 0,0279ψ2 + 0,6674ψ3);
C2 = 0;
C3 = X1(0,9415 +0,2697ψ - 0,4454ψ2 + 0,2354ψ3)};
{C1 = C1 + 1,132 X3;
C2 = C2 + 0,459 X3;
C3 = C3 + 0,525 X3;};
{C1 = C1 + 1,285 X4;
C2 = C2 + 1,562 X4;
C3 = C3 + 0,753 X4;};
{C1 = C1 + 1,365 X5;
C2 = C2 + 0,553 X5;
C3 = C3 + 1,730 X5;};
{C1 = C1 + 1,565 X6;
C2 = C2 + 1,267 X6;
C3 = C3 + 2,640 X6;};
{C1 = C1 + 1,046 X7;
C2 = C2 + 0,430 X7;
C3 = C3 + 1,120 X7}.