The theory of the finite element method deals very much with the problem of convergence, i.e. an asymptotic behavior of estimates of accuracy of an obtained approximate solution as the finite element mesh becomes infinitely dense. A number of important convergence theorems have been stated. For example, for consistent elements it has been determined [15, pp. 195–196] that if (k–1) is the degree of a polynomial used within a finite element for approximating its displacements and for obtaining an approximate solution of an elliptic boundary-value problem of order 2m expressed through the displacements uh, then the error of energy in comparison with the exact solution u is
\[ U(u-u_h,u-u_h)\leq Ch^{2(k-m) }\| u\|_k^2, \]
where h is the maximum value of the relative size of the element (the spacing of the mesh).
The following error estimates take place for s-th derivatives of z:
\[ \|u-u_h\|_s \leq Ch^{k-s} \|u\|_k, \quad if \quad s>2m-k; \]
\[ \|u-u_h\|_s \leq Ch^{2(k-s)} \|u\|_k, \quad if \quad s\leq 2m-k \]
Similar estimates for inconsistent elements have been obtained in a series of papers by I.D. Evzerov and V.S. Karpilovsky (see, for example, [5, 8]).
The data on the values of the convergence parameter enable to assign an approximate density of the finite element mesh on the basis of the following peculiar considerations [2, p.55]: “…let us just note that the convergence takes place assuming some natural limitations of initial data and the meshing of the area are satisfied, and the error of the determination of stresses/strains is of the order Сh/L where С denotes a constant depending on the shape of the area; h is the mesh spacing; L is a characteristic size of the area. This estimate should guide the definition of the mesh spacing, depending on the desired accuracy (average). For example, if you want the accuracy of the approximate solution to be 5%, choose the spacing of the mesh of around 1/20 of its characteristic size…”, i.e. a characteristic two-dimensional spot would include about 400 nodes, and in the case of a three-dimensional problem there would be about 8,000 nodes.
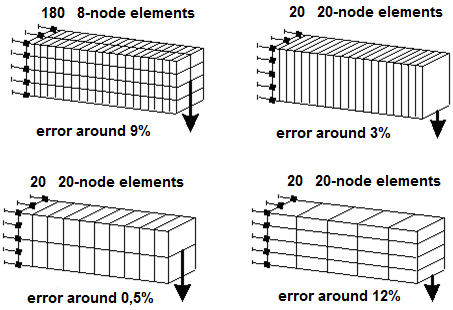
It should be remembered that the above consideration is true only in average, and the accuracy depends much not only on the finite element type (constants С and k) but also on the position of the finite elements and their orientation with respect to the flows of principal stresses. The latter fact can be seen from a characteristic example taken from the paper [7] and shown in Fig. 1.

Figure 1. Different finite element meshes and the accuracy of the analysis
One should remember that the afore-said estimates of the convergence rate are oriented at the determination of the asymptotic properties of the solution, while a practical designer is interested in the accuracy of an approximate solution obtained on a particular finite element mesh. Of course, in most cases the asymptotic convergence is accompanied by an appropriate “practical convergence”. The latter term will mean the possibility of obtaining an acceptable accuracy with a comparatively rough meshing. However, this rule has its exceptions too. In this regard, we would like to cite from a great mathematician and physicist A. Poincare (quoted from [1, p.52]):
“...of two series where their general terms are 1000n/n! and n!/1000n, mathematicians would name the first one to be convergent… because the millionth term is much less than 999,999th, whilst the second term would be treated as divergent for its general term may grow unlimitedly. Astronomers, on the contrary, would take the first series for a divergent one because its first 1,000 terms go increasing; and the second series would be called by them convergent because its first 1,000 terms go decreasing and this decrease is quick enough at the beginning.” And then follows a breathtaking conclusion: “Both views are valid: the first one in theoretical investigations, and the second one in computational applications”.
Apparently, when solving any responsible problem, an analysis of the solution quality must be performed. The solution can be checked by solving the problem repeatedly with a different finite element mesh. Certainly, it is hardly reasonable to solve a whole big problem on gradually thickening meshes, but this analysis obviously makes sense for characteristic fragments of a design model. The empirical fact of the solution stability at the mesh thickening is a rather convincing argument “pro” this approach.
All that has been said must not be treated as an appeal to the pure empiricism. Theoretical investigations of convergence are very important, and their results can be used in practice. However, there are some serious problems the designer should take into account. One of them is that a satisfactory practical convergence of displacements does not necessarily imply a good convergence of internal forces and stresses the designer is interested in. Those are determined by the differentiation of the displacements, and the differentiation is an incorrect operation in the sense that a slight variation of a function value may cause a substantial variation of the function derivative.
Thus, validation of practical convergence must be oriented at investigating results important for a particular problem to be solved. Here is, for example, a characteristic excerpt from a well-known monograph by O. Zenkevich: “The spacing of a mesh needed to obtain an acceptable accuracy in shell problems may depend on a number of reasons. It is often the case that a small thickness of the shell limits the area of bending moments to an edge zone where the moments change substantially. The membrane forces can be calculated with a high accuracy even on a rough mesh, while the variation of the bending moments require an extensively fine mesh for being described properly.” [6, p.257].
There is also a difficulty of comparing the stresses obtained on meshes of different densities: the stresses are often determined in centers of finite elements, and a certain effort is needed to compare stresses at the same points.
Moreover, when using some types of finite elements (such as triangular elements with the linear displacement approximation for plane elasticity), the stress fields are piecewise constant functions, and the areas of their constancy coincide with the mesh triangles. Values of the stresses determined with these elements vary intensively from one element to another, therefore usually one applies an averaging of the stresses by elements of a star and refers those to a nodal point. The comparison of such stress fields is encumbered with the operation of averaging.
Organizing the validation of the practical convergence, one should remember that the problem being solved may have unpleasant peculiarities due to an incorrect idealization of the structure. A typical example is the idealization of a load as a concentrated force (practically unfeasible situation) which may cause such features of the problem solution as infinitely big values (a logarithmic singularity in the expressions of bending moments in a plate under a concentrated force) or high gradients of the stress field.
Thus, the practical convergence check should be performed with examples similar to the problems of interest but having accurate solutions. In this case the interpretation of the testing results becomes more informative. Some problems of this kind are discussed in the next section.