Расчетная схема метода перемещений

Поскольку в основу используемых алгоритмов положен метод перемещений*, то идеализация конструкции должна быть выполнена в форме, приспособленной к использованию этого метода, а именно: система должна быть представлена в виде набора тел стандартного типа (стержней, пластин, оболочек и т.д.), называемых конечными элементами и присоединенных к узловым точкам.

* Имеется в виду общая система разрешающих уравнений, где неизвестными являются смещения и повороты узлов. Некоторые типы конечных элементов, такие, как гибридные элементы, внутри себя используют и силовые неизвестные, но они исключаются перед формированием общей системы уравнений.

Эти конечные элементы должны быть заранее изучены, чтобы иметь возможность определить их реакцию на единичные смещения и повороты узлов.

Узел в расчетной схеме метода перемещений представляется в виде абсолютно жесткого тела исчезающе малых размеров. Положение узла в пространстве при деформациях системы опре­деляется координатами центра и направлениями трех осей, жестко связанных с узлом. Иными словами, узел представляется как объект, обладающий шестью степенями свободы — тремя ли­нейными смещениями, определяемыми как разности координат в деформированном и неде­формированном состояниях, и тремя углами поворота. С узлами могут быть связаны и другие пара­метры, определяющие деформированное положение системы (дополнительные степени свободы).

В методе перемещений элементы системы считаются присоединенными только к узлам расчетной схемы. Указанная особенность построения расчетной схемы не всегда подчеркивается в учебной и справочной литературе. Такой подход является приближенным, поскольку, приводя эквивалентные усилия к узлам, условия равновесия конечных элементов некоторых типов (например, пластин и оболочек) можно выполнить только интегрально. На межэлементных границах нестержневых элементов мыслятся возможные разрезы, что заставляет обращать внимание на т.н. свойство совместности (конформности) элементов. Совместные элементы гарантируют совпадение перемещений и их необходимых производных для точек, расположенных на противоположных берегах разреза. Для несовместных элементов возникает необ­хо­димость выполнения дополнительных условий, компенсирующих возможные расхождения берегов разреза.

Следует отметить, что все представленные в библиотеке комплекса SCAD элементы либо являются совместными, либо для них гарантируется выполнение дополнительных условий компенсации несовместности.

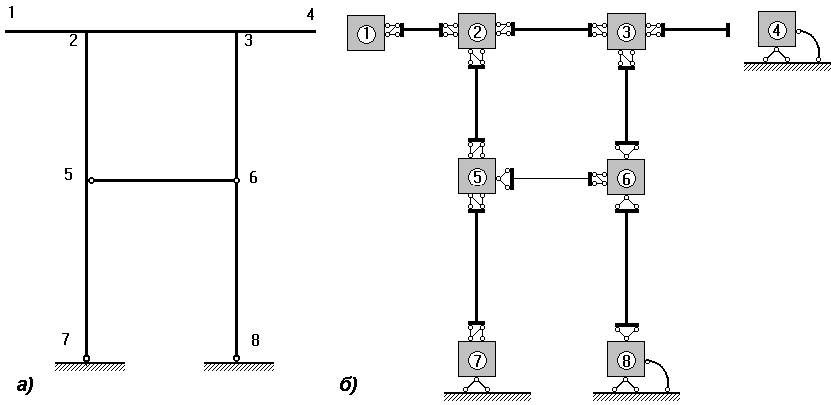
Рис. 1. Изображение расчетной схемы: а — традиционное; б — детальное

Условия примыкания элементов к узлам не всегда видно при использовании традиционных способов изображения расчетной схемы. Так, расчетная схема, показанная на рис. 1, а в традиционной форме, может навести на мысль о непосредственном соединении элементов одного с другим, в то время как более детальное изображение на рис. 1, б позволяет избежать такого заключения. Заметим также, что в детальном изображении видны и другие особенности реализации расчетной схемы, в частности, возможность выполнения одинаковых кинематических условий с использованием различных наборов связей (сравните узлы 1 и 4 или 7 и 8). Однако, этот прием не всегда безобиден. Например, с точки зрения кинематических свойств задачи два варианта расчетной модели, представленные на рис. 2, равноправны (балка, защемленная на левом конце и шарнирно опертая на правом).

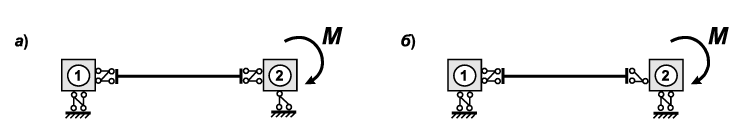
Рис. 2. Два варианта представления одной и той же расчетной схемы

Но с точки зрения задания усилий варианты различаются. Так, схема по рис. 2, а передает заданный внешний момент М на стержень, и узел 2 в этой схеме будет  иметь поворот, а схема по рис. 2, б не передает момент, и узел 2 этой схемы будет иметь нулевой угол поворота. Чтобы и в схеме по рис. 2, б возникал изгибающий момент в стержне, его следует считать не узловым, а приложенным к стержню в сечении около узла. С другой стороны, в схеме по рис. 2, а в результате расчета можно получить угол поворота в точке, где расположен узел 2, и он равен углу поворота правого концевого сечения стержня, а в схеме по рис. 2, б поворот концевого сечения не определяется, поскольку в комплексе SCAD предусмотрена выдача значений только для узловых перемещений и поворотов.

Предполагается, что вся расчетная схема состоит только из элементов заранее определенного типа. Список типов элементов, которыми оперирует вычислительный комплекс, может видоизменяться и по­полняться, однако каждой его конкретной версии соответствует определенный набор элементов — библиотека конечных элементов (БКЭ), из которой и выбираются «элементарные частицы» для форми­рования расчетных схем.

Наконец, следует заметить, что все узлы и элементы расчетной схемы нумеруются. Номера, при­своенные им, следует трактовать только как имена, которые позволяют делать необходимые ссылки. Например, можно указать узел, где приложена некоторая нагрузка, перечислить узлы, к которым при­соединен вполне конкретный элемент, составить список элементов, примыкающих к определенному узлу (это будет т. н. «звезда элементов» в узле) или входящих в определенную, назначенную нами, группу. Никаких других функций нумерация не выполняет, и она практически не влияет на время решения задачи благодаря имеющейся в комплексе возможности оптимизации профиля матрицы жесткости. Однако выдача результатов расчета чаще всего производится в порядке нумерации узлов (перемещения) или элементов (внутренние усилия), поэтому говорить о полной независимости от нумерации все же не приходится.