Стыковка элементов различной размерности
Лишь в редких случаях вся конструкция представлена элементами одинакового типа (например, только элементами плиты); чаще встречаются случаи, когда в одной расчетной модели присутствуют и стержневые, и оболочечные, и другие элементы.
Комплекс SCAD допускает почти произвольную комбинацию конечных элементов самых разнообразных типов, размерностей, размеров и геометрической формы, а также с различными числовыми характеристиками жесткости. Но эта программная гибкость таит в себе и опасности, иногда лежащие на поверхности, а иногда — скрытые и поэтому наиболее коварные. Такие ситуации возникают, например, при наличии в расчетной схеме одномерных (стержневых) и двумерных (плитных и/или оболочечных) элементов. Как будет показано ниже, такое объединение «разнокалиберных» элементов в общей расчетной схеме требует пристального внимания, в особенности — в местах соединения элементов различной размерности.
Стержни + плиты. В качестве примера комбинации плитных и стержневых элементов рассмотрим расчет пространственного стержневого каркаса совместно с плитным фундаментом.
Итак, рассмотрим дискретную расчетную схему, сочетающую в себе конечные элементы плиты и стержневые элементы, жестко присоединенные к плите (то, что плита расположена на упругом основании, не имеет значения для обсуждаемых здесь проблем). Сетка конечных элементов плиты выбирается так, чтобы стержни каркаса здания попадали в узлы сеточного разбиения плиты. Если не предпринимать никаких дополнительных мер, то описанная выше расчетная схема в узлах стыковки плитных и стержневых элементов обеспечит совместность как вертикальных перемещений плиты и каркаса (перемещений в направлении, перпендикулярном плоскости плиты), так и соответствующих углов поворота. Однако, получаемые в этой расчетной схеме изгибающие моменты в сечениях стоек, примыкающих к плите, не имеют отношения к истинному распределению внутренних усилий. А если это так, то это скажется и на распределении внутренних усилий в остальных элементах каркаса здания.
Действительно, представим себе, что сетка плиты сгущается и пользователь ожидает все большего уточнения результатов расчета. Однако, начиная с некоторой сеточной разбивки, дальнейшее дробление сетки приводит к уменьшению абсолютных значений изгибающих моментов в стержнях в местах их заделки в плиту. В пределе, при устремлении максимального размера сеточной ячейки к нулю эти изгибающие моменты также должны стремиться к нулю, а это означает, что данная расчетная схема обеспечивает не жесткое, а шарнирное присоединение элементов каркаса к плите. То, что пользователь формально при избранной им сетке получает некоторые отличные от нуля численные значения изгибающих моментов, свидетельствует лишь о погрешности дискретизации в методе конечных элементов, но нет же никаких оснований погрешность дискретизации принимать за достойный доверия результат!
В самом деле, изгибающий момент в стержне в описанной выше расчетной схеме, вне зависимости от размеров сетки, передается на плиту как момент, сосредоточенный в узле сетки. Но плита под действием сосредоточенного изгибающего момента получает бесконечный угол поворота в месте его приложения. Таким образом, плита не оказывает сопротивления на сосредоточенный поворот, а значит, и не защемляет элементов каркаса.
Для того чтобы откорректировать расчетную схему, следует рассмотреть конструктивное решение в месте прикрепления каркаса к плите. Если стойки каркаса присоединены к плите с помощью подколонников, то последние могут рассматриваться, например, как абсолютно жесткое тело, не меняющее своих размеров при любых изменениях сетки конечных элементов плиты.
Размеры же самого жесткого тела можно назначить, исходя из размеров подколонника (a×b) с учетом распределения давления от него на плиту под углом 45° до срединной поверхности плиты, что вполне отвечает традиционной инженерной практике. Эту ситуацию можно также смоделировать введением стержневой «подставки» (типа елочного крестика) из элементов достаточно большой жесткости.
|
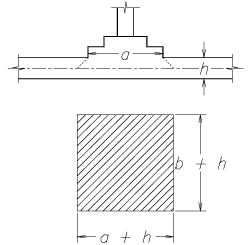
Рис. 1. Присоединение стойки через подколонник;
a и b — размеры подошвы подколонника в плане
|
В этой схеме сосредоточенный момент от стоек каркаса передается на плиту через жесткую шайбу, размеры которой a+h и b+h не связаны с размерами сетки конечных элементов, а значит, и с погрешностью дискретизации. Хотя погрешность дискретизации и будет влиять на численные значения изгибающих моментов в стойках, она не окажет такого катастрофического воздействия на отклонение расчетной схемы от реальной конструкции, как это было в исходной постановке задачи без введения в расчетную схему жесткого тела. В том случае, когда подколонники отсутствуют, можно в качестве размеров жесткого тела принять размеры поперечного сечения стойки с учетом 45-градусного распределения давления на плиту, как это показано на рис. 1.
|
Наконец, обратим внимание еще на одно обстоятельство, связанное с совместным расчетом пространственного каркаса и фундаментной плиты. Предполагая, что стойки каркаса ортогональны плоскости плиты, получим, что плита не оказывает сопротивления закручиванию стоек, а также смещениям v,w низа стоек в направлении осей Y, Z соответственно, поскольку у конечных элементов плиты просто нет соответствующих степеней свободы для сопротивления этим линейным перемещениям и закручиванию.
Если иных внешних горизонтальных связей (лежащих в плоскости Y, Z) расчетная схема не содержит, то механическая система окажется незакрепленной и геометрически изменяемой, так что программа вынуждена будет отреагировать на это обстоятельство.
Заметим, что для пространственного каркаса это не приводит к геометрической изменяемости системы, а у программы может и не быть механизмов обнаружения ошибок подобного рода. Это обстоятельство также необходимо иметь в виду при формировании расчетной схемы объединенной конструкции.
Стержни + балки-стенки. При расчете на горизонтальные нагрузки зданий повышенной этажности, содержащих в составе несущих конструкций как стержневой каркас, так и диафрагмы жесткости, в расчетную схему естественным образом входят разнородные элементы.
Если к формированию дискретной расчетной схемы подходить совершенно формально, описывая пластину совокупностью конечных элементов плоского напряженного состояния, а стержневой каркас одномерными элементами, и не предпринимать каких-либо дополнительных мер, то в ригелях, примыкающих к узлам сопряжения каркаса с диафрагмой, как изгибающие моменты, так и продольные и поперечные силы будут получаться какими угодно, но только не имеющими отношения к действительности.
Если для диафрагмы используются простейшие конечные элементы с двумя степенями свободы в узле (линейные перемещения u и v в двух взаимно ортогональных направлениях); тогда эти конечные элементы не окажут сопротивления повороту примыкающего к ним узла, поскольку у них (у элементов) просто отсутствуют соответствующие степени свободы, и, таким образом, эти конечные элементы не передадут на примыкающие узлы каких-либо моментных усилий. Поскольку расчетная программа потребует формального выполнения всех условий равновесия, в том числе и равновесия каждого из узлов по моментам, то отсюда примыкающие жестко к этим узлам ригели обязаны будут передать на узлы строго нулевые моменты. В результате изгибающие моменты в ригелях в этих узлах окажутся равными нулю, что соответствует расчетной схеме с шарнирным присоединением ригелей к диафрагме и не будет отвечать замыслу пользователя, сориентированного на защемление ригелей в диафрагме.
Каким же образом откорректировать исходную механическую модель или, что то же самое, математическую постановку задачи, позволяющую адекватно отобразить работу реальной конструкции? Как уже было сказано выше, для этого нужно детальнее рассмотреть конструктивные особенности сопряжения стержня и диафрагмы.
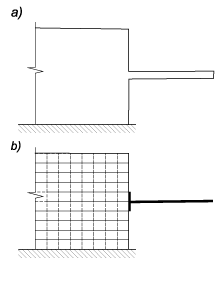
Пусть, например, стальной ригель двутаврового сечения заведен на части своей длины в кирпичную стену, как это показано на рис. 2, a. Тогда в расчетной схеме, в том числе и в дискретном ее аналоге, достаточно учесть проникающий на соответствующую длину в область плоской задачи одномерный элемент-стержень, как это показано на рис. 2, b.
|

|
|
|
Рис. 2. Заделка консоли в стенку
|
Рис. 3. Монолитное сопряжение
|
Иной вариант расчетной схемы можно предложить в случае монолитного сопряжения железобетонной стеновой панели и ригеля каркаса здания — рис. 3, a. Здесь можно учесть фактические размеры сечения — высоту ригеля, на протяжении которой вдоль границы стены уместно разместить абсолютно жесткое тело, как это показано на рис. 3, b. Это абсолютно жесткое тело для самого ригеля корреспондируется с гипотезой плоских сечений, согласно которой сечение ригеля остается после его деформации плоским и не изменяет своих размеров.
Разумеется, приведенные здесь два варианта формирования расчетных схем не исчерпывают всего многообразия возможных ситуаций, так что в каждом конкретном случае расчетчик должен исходить из конструктивных особенностей задачи, а не из неких заранее выдуманных, условных и подходящих на все случаи жизни схем.
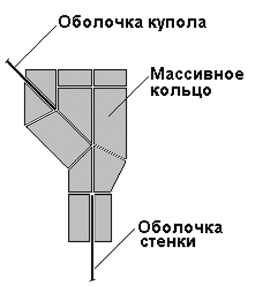
Прием «разноса области примыкания» по типу рис. 2 может использоваться и в других случаях сопряжения элементов различной размерности. На рис. 4 ниже показан пример такого сопряжения, в котором цилиндрическая оболочка стенки и сферическая оболочка крышки защитной конструкции атомного реактора сопрягается с массивным кольцом. Необходимо заметить, что в месте взаимопроникновения конструкций появляется некоторое возмущение жесткостных параметров за счет суммирования жесткостей оболочки и трехмерного тела в тех частях, которые занимают одно и то же положение в пространстве. Это следует учесть при назначении величин жесткости.
Рис. 4. Сопряжение стенки и крышки защитной оболочки реактора с массивным кольцом