Парирование изменяемости
В практических расчетах довольно часто случаются ошибки такого характера: расчетчик, прекрасно понимая, что схема работает по определенному закону деформирования (например, в одной плоскости) забывает, что системе сообщен другой признак типа схемы (например, пространственная система общего положения). Тогда конструкция оказывается изменяемой, и могут возникнуть некоторые неприятные явления. Типичным примером, где была допущена такая ошибка, является расчетная схема, изображенная на рисунке, где представлена фундаментная плита с примыкающими к ней стенами. Схема была геометрически изменяемой, и в ней были возможны смещения системы в целом как жесткого тела по направлениям осей X и Y.
|
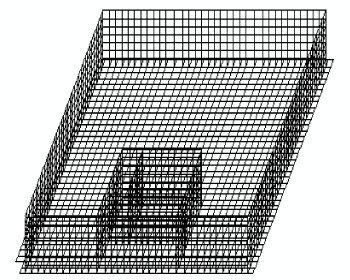
Расчетная схема
|
Результаты расчета изменяемой системы показали ошибку контроля точности решения 99%. Это связано с тем, что, несмотря на то, что комплекс SCAD устраняет геометрическую изменяемость самостоятельно в процессе решения, такая процедура может привести к потере точности за счет неудачной стратегии устранения изменяемости. Лучше устранить изменяемость аккуратно. Так, в рассматриваемом случае следует запретить перемещения системы как жесткого целого, для чего рекомендуется использовать внешне статически определимую систему закреплений.
После внесения этих изменений в расчетную схему никаких проблем с точностью решения не возникло.
|
Процедура наложения узловых связей с точки зрения техники ее выполнения несложна. Проблемой может стать рациональное назначение тех связей, необходимость учета которых связана с изменяемостью рассматриваемой расчетной схемы или ее фрагмента. Типичным примером может служить расчет плиты на упругом основании, которая вполне достаточно раскреплена из плоскости изгиба, но в плоскости может перемещаться как жесткое тело. Расчетчик понимает, что закрепление такой плиты в плоскости является необходимым, но не всегда верно выбирает удачный вариант такого раскрепления.
Во-первых, раскрепление желательно сконструировать таким образом, чтобы система была внешне статически определимой (в плоскости плиты следует расположить три связи). Если это удастся сделать, то реакции в дополнительно наложенных связях должны оказаться нулевыми из-за того, что отсутствуют нагрузки в плоскости плиты. Это рассуждение верно лишь теоретически, поскольку не учитывает неизбежную погрешность численного решения. Накопление ошибок округления приводит к тому, что вместо нулевой реакции мы получаем малые, но все же ненулевые значения реакций. Это свидетельствует о том, что в реальном численном представлении дело обстоит так, как если бы имела место некоторая небольшая ненулевая сила, действующая в плоскости плиты.
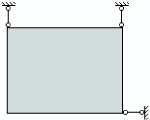
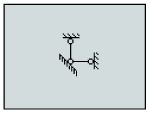
Поскольку упомянутая сила воспринимается условно наложенными связями, то значения полученных реакций оказываются зависящими от способа наложения связей. Если такие связи расположить по возможности далеко одна от другой (рис. а), реакции окажутся малыми и не внесут заметного возмущения в напряженное состояние. Если же, например, закрепить плиту в одной точке (рис. б) от двух смещений и поворота, что теоретически является возможным, возмущение может оказаться заметным, и результаты расчета в окрестности такого узла окажутся искаженными.
|
а)
|
б)
|
Наложение связей, парирующих изменяемость:
а — рекомендуемая схема; б — неудачное раскрепление
Все сказанное выше относится к любому случаю раскрепления свободного (имеющего свободу перемещений как жесткого тела) фрагмента системы.


