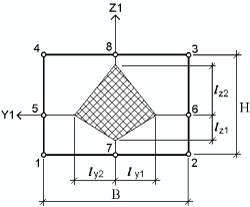
В качестве критерия определения РСУ здесь приняты экстремальные значения нормальных и касательных напряжений в контрольных точках сечения (рис. 1).

Рис. 1. Прямоугольник, ограничивающий габариты произвольного сечения
Для нормальных напряжений используется формула:
| \[ \sigma_{k} =\frac{N}{F}\pm \frac{M_{y} z_{k} }{I_{y} }\pm \frac{M_{z} y_{k} }{I_{z} } \] | (1) |
где k — точка сечения стержня (k = 1...8).
Такой подход позволяет определить экстремальные нормальные напряжения в сечении любой формы.
Для касательных напряжений используется приближенная формула:
| \[ \tau_{y} =\frac{1}{F}\left(\frac{Q_{y} }{2}\pm \frac{M_{kp} }{2(l_{y1} +l_{y2} )}\right) \quad \tau_{z} =\frac{1}{F} \left(\frac{Q_{z} }{2}\pm \frac{M_{kp} }{2(l_{z1} +l_{z2} )}\right), \] | (2) |
где ly,i и lz,i ядровые расстояния в сечении стержня (i = 1, 2).
Нумерация критериев и соответствующих им напряжений, вычисленных по формулам (1, 2) приведена в табл. 1.
Кроме того анализируются экстремальные положительные и отрицательные значения напряжений от продольной силы (критерии под номерами 17 и 18), напряжения от перерезывающих сил (критерии под номерами 27...34), максимальные и минимальные значения изгибающих моментов (критерии под номерами 51...54), которые используются при подборе арматуры в элементах железобетонных конструкций и проверке несущей способности элементов стальных конструкций.
Таблица 1
Критерий |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Значение |
σ1+ |
σ1- |
σ2+ |
σ2- |
σ3+ |
σ3- |
σ4+ |
σ4- |
τy7+ |
τy7- |
Критерий |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Значение |
τy8+ |
τy8- |
τz5+ |
τz5- |
τz6+ |
τz6- |
N+ |
N- |
σ7+ |
σ7- |
Критерий |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Значение |
σ8+ |
σ8- |
σ5+ |
σ5- |
σ6+ |
σ6- |
Qy+ |
Qy- |
Qy+ |
Qy- |
Критерий |
|
|
|
|
|
|
31 |
32 |
33 |
34 |
Значение |
|
|
|
|
|
|
Qz+ |
Qz- |
Qz+ |
Qz- |
Критерий |
|
|
|
|
|
|
51 |
52 |
53 |
54 |
Значение |
|
|
|
|
|
|
My+ |
My- |
Mz+ |
Mz- |
Для поиска невыгодного значения эксцентриситета используется критерий
| \[ \sigma =\frac{1}{F}\left(N\pm \frac{M_{y} }{l_{z,i} }\sin \frac{n\pi }{8}\pm \frac{M_{z} }{l_{y,i} }\sin \frac{m\pi }{8}\right), \] | (3) |
где n, m=0, 1, 2, 3, 4.
Данный критерий важен для железобетонных конструкций.
Критерии, вычисленные по формуле (3), имеют трехзначные номера в соответствии с табл. 2.
Таблица 2
Номер критерия |
1nm |
2nm |
3nm |
4nm |
5nm |
6nm |
7nm |
8nm |
Значение |
σ++ |
-σ++ |
σ+– |
-σ+– |
σ–+ |
-σ–+ |
σ–– |
-σ–– |
Так, например, критерий с номером 532 означает максимальное значение величины
\[ N-\frac{M_{y} }{l_{z,i} }\,\;\sin \frac{3\pi }{8}+\frac{M_{z} }{l_{y,i} }\,\;\sin \frac{2\pi }{8}. \]