Назначение характеристик динамического загружения

Исходные данные для расчета задаются в многостраничном диалоговом окне Параметры динамических воздействий, которое вызывается кнопкой  из раздела Загружения инструментальной панели препроцессора. В группе Вид воздействия следует активизировать маркер Прямое интегрирование, после чего становится доступной одноименная страница.

Для выполнения расчета необходимо задать следующие данные:

• шаг интегрирования;
• продолжительность процесса;
• данные о модальном демпфировании, которые могут задаваться путем указания параметров демпфирования (в долях от критического) для первых двух собственных форм. В качестве альтернативного способа предусмотрено явное задание пользователем коэффициентов α и β (при активном маркере Задание самостоятельно). Используя кнопку , можно активировать диалоговое окно, которое позволяет ввести две собственные частоты и соответствующие параметры модального демпфирования. Нажатие кнопки ОК приведет к вычислению коэффициентов α и β и автоматической записи этих величин в соответствующие поля ввода; кроме того, учет демпфирования может быть произведен на основании данных о демпфировании материалов (в жесткостных характеристиках конечных элементов для этого следует задать параметр затухания;
• список моментов времени, в которых выполняется вывод результатов;
• параметр \(\alpha-HHT\) метода.

В строках таблицы задается следующая информация:

• время запаздывания – интервал времени, позволяющий сдвигать заданную нагрузку во времени относительно момента начала процесса интегрирования;
• масштабный множитель, на который умножается интенсивность нагрузки в каждый момент времени;
• номер и название ссылочного статического загружения;
• полный путь и название текстового файла, задающего функцию времени φp(t).

Если при задании моментов времени для выдачи результатов время процесса еще не исчерпано, то шаг выдачи следующих результатов определяется как разность между двумя последними заданными значениями. Например, пусть продолжительность процесса составляет 1 с, а в окне «Моменты времени для выдачи результатов» указано 0 0.02 0.03. Результаты расчета будут сохранены в моменты времени 0, 0.02 с 0.03 с 0.04 с 0.05 с ... 1 с . Первые три момента времени явно заданы пользователем, а каждый из последующих моментов времени определяется как предыдущий плюс приращение, где приращение вычисляется как 0.03 – 0.02 = 0.01 с . Отсюда следует, что в окне «Моменты времени для выдачи результатов» как минимум должно быть указано два момента времени.

Для задания динамического загружения необходимо прежде всего задать ссылочные статические нагрузки точно так, как это делается для обыкновенных статических нагрузок. При этом возможно задавать не только узловые силы, но и сосредоточенные силы и распределенные нагрузки, приложенные к конечным элементам между узлами, а также вынужденные смещения опор, что позволяет производить расчет конструкций на сейсмические воздействия.

Для задания динамических нагрузок необходимо выполнить следующие действия:

• нажать кнопку Добавить, после чего в таблице с описанием нагрузок появится новая строка;
• в графе № статического загружения выбрать из выпадающего списка статическое загружение, на основании которого будет генерироваться изменяемая во времени нагрузка;
• в графе Множитель задать масштабный множитель μ1;
• в графе Запаздывание указать время запаздывания t10;
• нажатием кнопки  выбрать текстовый файл, задающий функцию φ1(t) (по умолчанию файл имеет расширение .thi);
• если необходим ввод второй составляющей, нажать кнопку Добавить, после чего в таблице появится новая строка, и повторить перечисленные выше действия.

Для контроля графика функции времени используется кнопка , нажатие которой приводит к появлению диалогового окна Функция времени. Кнопки  в строках таблицы позволяют выбрать и заменить соответствующий текстовый файл с функцией времени.

Содержимое каждого текстового файла с функцией времени копируется и хранится "внутри" файла модели. Поэтому для переноса данных на другой компьютер достаточно скопировать только spr-файл. При этом может возникнуть ситуация, при которой указанный ранее путь уже не соответствует текущему положению файла. В этом случае строка таблицы принимает вид:

Два вопросительных знака и красный цвет имени файла указывает на отсутствие файла на диске, а кнопка  позволяет сохранить функцию времени в файле на внешнем диске (для этого используется стандартный диалог Сохранить для выбора места хранения).

Для удаления какой-либо составляющей динамической нагрузки из списка необходимо курсором мыши выбрать соответствующую строку списка и нажать кнопку Удалить.  Информация о динамическом загружении запишется в модель при выходе из диалогового окна нажатием кнопки OK.

В графе Сглаживание по умолчанию используется опция «линейная интерполяция». Дело в том, что значения функции времени \( f_{s} \left( {t-t_{0}^{s} } \right) \) задаются в отдельные моменты времени. В процессе численного интегрирования необходимо выполнить интерполяцию – определить значение функции времени между узлами интерполяции – моментами времени, в которых задана функция \( f_{s} \left( {t-t_{0}^{s} } \right) \). Для подавляющего большинства задач вполне достаточно применить линейную интерполяцию. Однако в случае вынужденного смещения опор (сейсмический анализ) может оказаться, что линейная интерполяция является слишком «жесткой» и возбуждает паразитные высокие частоты в силу того, что скорости \( \dot{{f}}_{s} \left( {t-t_{0}^{s} } \right) \) в узлах интерполяции претерпевают разрывы, а ускорения \( \ddot{{f}}_{s} \left( {t-t_{0}^{s} } \right) \) равны нулю на всем интервале интерполяции между узлами, а в узлах интерполяции представляются дельта-функциями Дирака [6].

В таком случае надо применить сглаживание, а возможно, и подавление высоких мод с помощью α– HHT метода. Для сглаживания выбираем опцию «Кубическая парабола» либо «Полином Эрмита». И в том, и в другом случае между узлами интерполяции функция времени \( f_{s} \left( {t-t_{0}^{s} } \right) \) будет аппроксимироваться полиномом третьей степени, функция скоростей \( \dot{{f}}_{s} \left( {t-t_{0}^{s} } \right) \) – полиномом второй степени, а ускорения \( \ddot{{f}}_{s} \left( {t-t_{0}^{s} } \right) \) – линейной интерполяцией. В узлах интерполяции функции \( f_{s} \left( {t-t_{0}^{s} } \right) \), \( \dot{{f}}_{s} \left( {t-t_{0}^{s} } \right) \), \( \ddot{{f}}_{s} \left( {t-t_{0}^{s} } \right) \) не имеют разрывов. Опция «Кубическая парабола» применима только для сейсмического анализа. Входным воздействием является заданная акселерограмма. В процессе интегрирования уравнений движения SCAD автоматически определяет скорости и перемещения. Опция «Полином Эрмита» применима для любых видов динамического воздействия. В этом случае входным воздействием является функция вынужденных перемещений (функция времени \( f_{s} \left( {t-t_{0}^{s} } \right) \)). В случае сейсмики заданную акселерограмму необходимо два раза проинтегрировать, используя редактор акселерограмм.

Пример текстового файла, задающего функцию времени φp(t):

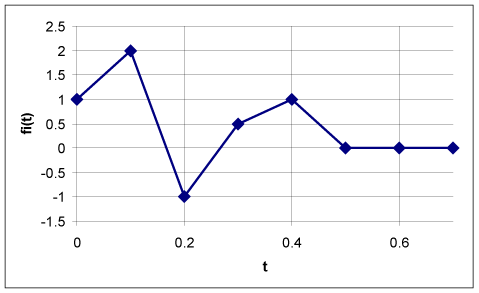
Рис. 1

На рис. 1 изображена приведенная в таблице зависимость φp(t) для моментов времени t ≤ 0.7. Если шаг интегрирования не совпадает с моментом времени, в котором задана функция времени, по умолчанию выполняется линейная интерполяция. Это следует принимать во внимание при задании нагрузок, быстро осциллирующих во времени.

Можно задавать также зависимости  φp(t) с переменным по времени шагом:

Пример текстового файла, задающего функцию времени φp(t) с переменным шагом:

При линейной интерполяции функции времени, относящейся к заданным перемещениям, в численном решении для ускорений в узлах, соседних с теми, в которых заданы вынужденные перемещения, могут возникнуть паразитные высокочастотные осцилляции. Для подавления этих осцилляций используется два подхода. Первый основан на \(\alpha-HHT\) методе [3], подавляющий высокочастотные колебания при ω Δt≥ 1, где ω – частота соответствующего тона, а Δt– шаг интегрирования по времени. При этом колебания с частотами ω Δt< 1 получаются достоверными. Степень подавления зависит от параметра \(\alpha\), \(\alpha\in [0, – 1/3]\). Если \(\alpha=0\), то подавление высоких частот отсутствует, и \(\alpha-HHT\) метод переходит в метод Ньюмарка. Максимальное подавление осуществляется при \(\alpha=-1/3\).

Второй подход основан на интерполяции заданной функции времени кубической параболой либо полиномами Эрмита. Если пользователь задает акселерограмму (зависимость ускорений от времени), то в таблице с параметрами статических загружений в графе Сглаживание необходимо выбрать признак «Кубическая парабола». Сейсмограмма будет получена автоматически в процессе решения задачи при использовании интерполяции перемещений полиномом третьей степени. Скорости при этом интерполируются с помощью полинома второй степени, а для ускорений используется линейная интерполяция. Этот способ применим только для сейсмического анализа.

Если сейсмограмма (зависимость перемещений от времени) получена с помощью редактора акселерограмм, то в графе Сглаживание необходимо выбрать признак «Полиномы Эрмита». В этом случае перемещения будут интерполированы полиномами третьей степени, скорости – полиномами второй степени, а ускорения – с помощью линейной интерполяции. Это способ применим для всех видов динамической нагрузки.

При выборе признака «Линейная интерполяция» заданная функция времени интерполируется полиномом первой степени. Если это функция зависимости перемещений от времени, то ее первая производная (скорости) интерполируется кусочно-постоянной функцией, а вторая производная (ускорения) между узлами интерполяции равна нулю, а в узлах интерполяции (в заданные моменты времени) представляется в виде дельта-функций Дирака. В случае, если задается смещение опор, такая интерполяция приводит к тому, что система движется рывками, которые и порождают упомянутые выше паразитные высокочастотные колебания.

Для каждой конкретной задачи следует выбрать, какой из приемов следует использовать, причем допускается одновременное применение как \(\alpha-HHT\) метода, так и интерполяции высокого порядка.

Для того, чтобы за данным нелинейным статическим анализом был выполнен нелинейный динамический анализ, необходимо перевести включить маркер Нелинейный анализ. При этом все нагрузки, прикладываемые на этапе статического анализа, передаются в динамический анализ, поэтому на этапе динамического анализа их прикладывать уже не надо. Данная реализация алгоритма соответствует решению задачи статики от действия статических нагрузок на первом этапе, а затем – задачи Коши на втором. Кроме того, этапу динамического анализа как начальное состояние передается напряженно-деформируемое состояние всех нелинейных конечных элементов, полученных в конце этапа статического анализа. Поскольку решается нелинейная задача, то принцип суперпозиции неприменим, и решение динамической задачи «отсчитывается» от решения статической задачи.

При нажатии на кнопку Игнорировать силы инерции и диссипации выполняется статический анализ, использующий алгоритм интегрирования уравнений движения. В ряде случаев этот алгоритм оказывается удобнее статического, особенно при многопараметрическом нагружении. Далее необходимо задать максимальное количество итераций метода Ньютона-Рафсона на данном шаге по времени и допускаемую величину ошибки при подавлении невязки в процессе итераций корректора. Если опция Факторизовать тангенциальную матрицу жесткости на каждой итерации включена, то реализуется метод Ньютона-Рафсона. В противном случае сборка и разложение тангенциальной матрицы жесткости производится только на первой итерации (модифицированный метод Ньютона-Рафсона). Обычно при учете физической нелинейности требуется факторизация тангенциальной матрицы жесткости на каждой итерации. Подробное описание реализованного алгоритма решения нелинейной задачи Коши приведено в [5].

Если маркер Явный метод интегрирования включен, выбирается явный метод интегрирования, представляющий собой объединение подходов [3, 7].

Явный метод интегрирования для некоторых задач может оказаться более эффективным, чем неявный, не требует сборки и разложения матрицы тангенциальной жесткости и в случае значительного разрушения элементов конструкций может оказаться значительно более стабильным, чем неявный. С другой стороны, явный метод требует обычно задания значительно меньшего шага интегрирования, чем неявный, а также матрица масс должна быть только диагональной и при этом не должна быть особенной. Это означает, что на степенях свободы, соответствующих как поступательным перемещениям, так и углам поворота, не должно быть нулевых инерционных параметров.

Обычно в расчетных моделях МКЭ с диагональной матрицей масс на вращательных степенях свободы находятся нулевые элементы. Поэтому при использовании явного метода производится регуляризация матрицы масс, и параметр регуляризации γ, обычно принимаемый в пределах [0.0001, 0.1] задает значения фиктивных величин γ∙max{M}, добавляемых к нулевым элементам диагональной матрицы масс. Здесь max{M} – наибольший элемент исходной матрицы масс. Если текущий элемент матрицы масс исходной расчетной модели отличен от нуля, то он остается без изменений. Чем меньше γ, тем меньше искажается исходная матрица масс, но тем меньший шаг интегрирования Δt требуется для обеспечения устойчивости численного решения.

Увеличение количества итераций явного метода на каждом временном шаге Δt повышает точность решения, однако увеличивает время счета, поскольку на каждой итерации вычисляются внутренние силы системы.

Рекомендуется начать анализ с величин параметров, установленных по умолчанию.

Если маркер Нелинейный анализ отключен, за данным нелинейным статическим анализом выполняется линейный анализ интегрирования уравнений движения. В этом случае нагрузки и напряженно-деформированное состояние конечных элементов в динамический анализ не передается, а результаты динамического анализа отсчитываются от недеформированного состояния. Влияние нелинейного статического анализа на последующий линейный динамический обусловлено только тем фактом, что динамический анализ использует матрицу тангенциальной жесткости, полученную в конце нелинейного статического анализа – рассматриваются малые линейные колебания относительно положения статического равновесия, определенного на этапе нелинейного статического анализа. При этом все нелинейные конечные элементы подменяются их линейными аналогами.