Особенностями данной постановки задачи является то, что перемещения, скорости и ускорения узлов конечно-элементной модели определяются в абсолютной системе отсчета, связанной с условно неподвижной землей. Сейсмическое воздействие задается как вынужденные смещения опор, поэтому входной информацией являются не акселерограммы, а сейсмограммы (зависимость перемещений от времени), получающиеся из акселерограмм двойным интегрированием по времени. Такой подход позволяет естественным образом решать задачи с асинхронным возмущением опор. Для получения виброграмм из заданных акселерограмм рекомендуется использовать Редактор Акселерограмм SCAD.
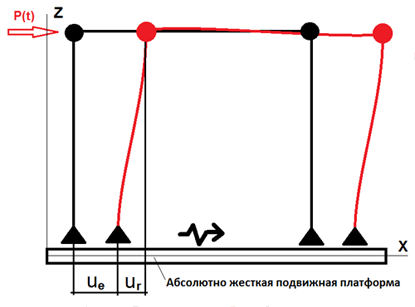
На рис. 1, 2 представлены соответственно традиционная постановка задачи в системе отсчета, связанной с абсолютно жестким подвижным основанием, и постановка задачи в абсолютной системе отсчета, используемая в SCAD.

Рис. 1. Решение задачи в относительной системе отсчета, связанной с абсолютно жесткой подвижной платформой, совершающей поступательное движение (классическая постановка)
\[ \left\{ {{\begin{array}{*{20}c} {{\rm {\bf u}}={\rm {\bf u}}_{e} +{\rm {\bf u}}_{r} ;} \\ {{\rm {\bf \ddot{{u}}}}={\rm {\bf \ddot{{u}}}}_{e} +{\rm {\bf \ddot{{u}}}}_{r} ;} \\ {{\rm {\bf M\ddot{{u}}}}_{r} +{\rm {\bf Ku}}_{r} =-{\rm {\bf M\ddot{{u}}}}_{e} \left( t \right)+{\rm {\bf p}}\left( t \right)} \\ \end{array} }} \right. \]
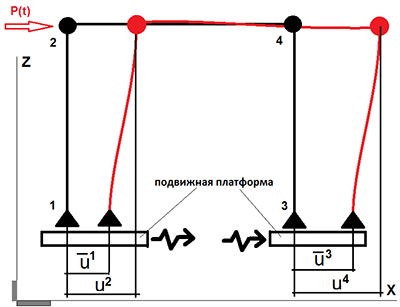
Рис. 2. Решение задачи относительно условно неподвижной абсолютной системы отсчета (SCAD)
Уравнения движения конечно-элементной (МКЭ) модели в абсолютно неподвижной системе отсчета представлены в виде:
\[ \underbrace {\left( {{\begin{array}{*{20}c} {{\rm {\bf M}}_{11} } & 0 \\ 0 & {{\rm {\bf M}}} \\ \end{array} }} \right)}_{{\rm {\bf \hat{{M}}}}}\cdot \left( {{\begin{array}{*{20}c} {{\rm {\bf \ddot{{\bar{{u}}}}}}} \\ {{\rm {\bf \ddot{{u}}}}} \\ \end{array} }} \right)+\underbrace {\left( {{\begin{array}{*{20}c} {{\rm {\bf K}}_{11} } & {{\rm {\bf K}}_{12} } \\ {{\rm {\bf K}}_{21} } & {{\rm {\bf K}}} \\ \end{array} }} \right)}_{{\rm {\bf \hat{{K}}}}}\cdot \left( {{\begin{array}{*{20}c} {{\rm {\bf \bar{{u}}}}} \\ {{\rm {\bf u}}} \\ \end{array} }} \right)+\underbrace {\left( {{\begin{array}{*{20}c} {{\rm {\bf C}}_{11} } & {{\rm {\bf C}}_{12} } \\ {{\rm {\bf C}}_{21} } & {{\rm {\bf C}}} \\ \end{array} }} \right)}_{{\rm {\bf \hat{{C}}}}}\cdot \left( {{\begin{array}{*{20}c} {{\rm {\bf \dot{{\bar{{u}}}}}}} \\ {{\rm {\bf \dot{{u}}}}} \\ \end{array} }} \right)=\left( {{\begin{array}{*{20}c} 0 \\ {{\rm {\bf p}}(t)} \\ \end{array} }} \right)\quad , \] |
(1) |
где \( {\rm {\bf \hat{{K}}}},\;{\rm {\bf \hat{{M}}}},\;{\rm {\bf \hat{{C}}}} \) – соответственно матрицы жесткости, масс и диссипации, охватывающие степени свободы, подлежащие определению (вектор узловых значений неизвестных u), а также известные перемещения в узлах – вынужденные смещения \( {\rm {\bf \bar{{u}}}}(t), \quad {\rm {\bf p}}(t) \) – заданные силы.
Из выражения (1) следует:
| \[ {\rm {\bf M{\ddot{u}}}}+{\rm {\bf C{\dot{u}}}}+{\rm {\bf Ku}}=-{\rm {\bf K}}_{21} {\rm {\bf \bar{u}}}\left( t \right)-{\rm {\bf C}}_{21} {\rm {\bf \dot{\bar{u}}}}\left( t \right)+{\rm {\bf p}}\left( t \right) \] | (2) |
Здесь в левой части уравнения находятся ускорения, скорости и перемещения, подлежащие определению, а в правой части – известные величины.
В настоящее время реализованы два различных подхода для учета диссипации. Первый подход основан на гипотезе Рэлея, а второй – на учете внутреннего сопротивления материала.
Согласно гипотезе Рэлея,
| \[ {\rm {\bf \hat{{C}}}}=\alpha \cdot {\rm {\bf \hat{{M}}}}+\beta \cdot {\rm {\bf \hat{{K}}}}, \] | (3) |
где α, β – коэффициенты пропорциональности, причем слагаемое \( \alpha \cdot \bf\hat{{M}} \) отвечает за демпфирование нижних мод, а слагаемое \( \beta \cdot \bf\hat{{K}} \) – верхних. Такое представление предполагает возможность разделения системы уравнений при разложении нагрузки по формам собственных колебаний недемпфированной системы [1], [2].
Подставляя (3) в (2), получаем:
| \[ {\rm {\bf M}}\left( {{\rm {\ddot{\bf {u}}}}+\alpha \cdot {\rm \dot{{\bf {u}}}}} \right)+{\rm {\bf \tilde{{C}}\dot{{u}}}}+{\rm {\bf K}}\left( {{\rm {\bf u}}+\beta \cdot {\rm \dot{{\bf {u}}}}} \right)=-{\rm {\bf K}}_{21} \left( {{\rm {\bf \bar{{u}}}}+\beta \cdot {\rm {\bf \dot{{\bar{{u}}}}}}} \right)-{\rm {\bf \tilde{{C}}}}_{21} {\rm \dot{{\bf {\bar{{u}}}}}}+{\rm {\bf p}}(t) \] | (4) |
Здесь К, М – традиционные матрицы жесткости и масс, охватывающие только степени свободы, подлежащие определению, \( \bf \tilde{C} \) – матрица диссипации, обусловленная локальными демпферами (см. раздел 1.6).
В случае не рэлеевского демпфирования (учет внутреннего сопротивления материала) матрица диссипации представляется так:
| \[ {\rm {\bf C}}=\sum\limits_{e=1}^{N_{e} } {\gamma_{e} {\rm {\bf P}}_{e}^{T} } {\rm {\bf K}}_{e} {\rm {\bf P}}_{e} \] | (5) |
где суммирование выполняется по всем конечным элементам расчетной модели Ne, γe – коэффициент внутреннего неупругого сопротивления материала, Ke – матрица жесткости конечного элемента e, Pe – матрица перестановок, выполняющая рассылку элементов матрицы жесткости Ke конечного элемента eв позиции элементов глобальной матрицы жесткости K. При этом матрица диссипации C является симметричной разреженной матрицей, имеющей ту же ненулевую структуру, что и матрица жесткости K. Данный подход позволяет учесть многокомпонентное демпфирование, когда конечные элементы расчетной модели в случае разных материалов имеют различные значения γe. При этом матрица диссипации C не может быть представлена в виде линейной комбинации матриц K и M, и применение метода разложения по формам собственных колебаний не приводит к разделению уравнений движения на отдельные несвязанные уравнения для каждой моды. Поэтому для решения задачи (2) мы применяем методы прямого интегрирования.
Подчеркнем, что одновременное задание рэлеевского демпфирования и не рэлеевского возможно только при использовании рэлеевского демпфирования и локальных демпферов. Одновременное использование рэлеевского демпфирования и модели диссипации на основе внутреннего неупругого сопротивления невозможно – если в диалоге «Параметры динамических воздействий» выбрать «Демпфирование материала», то рэлеевское демпфирование будет проигнорировано. Поэтому при использовании данной модели диссипации параметры демпфирования должны быть заданы для каждого материала.
Обозначим \( {\rm {\bf \bar{{u}}}}=\sum\limits_{s=1}^{M_{s} } {\mu_{s} \cdot {\rm {\bf k}}_{s} \cdot f_{s} \left( {t-t_{0}^{s} } \right)} ,\quad {\rm {\bf \dot{{\bar{{u}}}}}}=\sum\limits_{s=1}^{M_{s} } {\mu_{s} \cdot {\rm {\bf k}}_{s} \cdot \dot{{f}}_{s} \left( {t-t_{0}^{s} } \right)} \), где ks – векторы пространственной конфигурации, задающие форму вынужденных смещений, fs(t) – функция, задающая закон изменения нагрузки во времени, s = 1, 2, ..., Ms – ссылочные загружения или просто ссылки – номера статических загружений при расчете на вынужденные смещения. Аналогично \( {\rm {\bf p}}\left( t \right)=\sum\limits_{p=1}^{N_{p} } {\mu_{p} \cdot {\rm {\bf k}}_{p} \cdot f_{p} \left( {t-t_{0}^{p} } \right)} \). Здесь p = 1, 2, ..., Np – ссылочные загружения или просто ссылки – номера статических загружений при расчете на силовые воздействия, kp – векторы пространственной конфигурации нагрузки. Величины \( \mu_{s} ,\;t_{0}^{s} , \quad \mu_{p} ,\;t_{0}^{p} \) означают соответственно масштабные множители и время запаздывания.
Будем называть каждое слагаемое приведенных выше сумм соответственно s-й или p-й составляющей динамического загружения.
Обозначим bs= -K21·ks, cs= -C21·ks, s = 1, 2, ..., Ms· Дополняя полученное выше дифференциальное уравнение начальными условиями, получаем
| \[ \left\{ {{\begin{array}{*{20}c} {{\rm {\bf M\ddot{{u}}}}+{\rm {\bf C\dot{{u}}}}+{\rm {\bf Ku}}=\sum\limits_{s=1}^{M_{s} } {{\rm {\bf b}}_{s} \cdot \mu_{s} \cdot f_{s} \left( {t-t_{0}^{s} } \right)} +\sum\limits_{s=1}^{M_{s} } {{\rm {\bf c}}_{s} \cdot \mu_{s} \cdot \dot{{f}}_{s} \left( {t-t_{0}^{s} } \right)} +\sum\limits_{p=1}^{N_{p} } {{\rm {\bf k}}_{p} \cdot \mu_{p} \cdot f_{p} \left( {t-t_{0}^{p} } \right)} } \\ {{\rm {\bf u}}\left( 0 \right)={\rm {\bf u}}_{0} } \\ {{\rm {\bf \dot{{u}}}}\left( 0 \right)={\rm {\bf \dot{{u}}}}_{0} } \\ \end{array} }} \right. \] | (6) |
Здесь матрица C представляет как объединение рэлеевского демпфирования с локальными демпферами (если последние имеются), так и объединение демпфирования материала с локальными демпферами.
В случае рэлеевского демпфирования коэффициенты α и β могут быть вычислены по формулам| \[ \alpha =\frac{2\omega_{i} \omega_{j} \left( {\xi_{i} \omega_{j} -\xi _{j} \omega_{i} } \right)}{\omega_{j}^{2} -\omega_{i}^{2} }, \quad \beta =\frac{2\left( {\xi_{j} \omega_{j} -\xi_{i} \omega_{i} } \right)}{\omega_{j}^{2} -\omega_{i}^{2} }, \] | (7) |
где ωi, ωj, – две собственные циклические частоты [рад/с] для форм колебаний i и j , а ξi, ξj - модальное демпфирование, заданное в процентах от критического демпфирования. Предполагается, что ωj > ωi > 0 и ξj ≥ ξi > 0.
Если принять i = 1, j = 2, то
| \[ \alpha =\frac{2\omega_{1} \omega_{2} \left( {\xi_{1} \omega_{2} -\xi _{2} \omega_{1} } \right)}{\omega_{2}^{2} -\omega_{1}^{2} }, \quad \beta =\frac{2\left( {\xi_{2} \omega_{2} -\xi_{1} \omega_{1} } \right)}{\omega_{2}^{2} -\omega_{1}^{2} } \] | (8) |
В случае, когда ω2 = ω1 или первые две частоты очень близки ( \( \frac{\omega_{2} -\omega_{1} }{\omega_{1} } \le 0.0001 \) принимается, что α = 2ξ1ω1, а β=0.
Начальные условия определяются начальными перемещениями системы (вектор \( \bf{u_0} \)) и начальными скоростями (вектор \( {\rm {\bf \dot{u}}}_{0} \)). В текущей реализации принято \( {\bf u_{0} = {\bf \dot{\bf u}}}_{0} = 0 \).
Метод решения. Для решения задачи используется α–HHT метод в форме «предиктор-корректор» [3], [5], [6]. Параметр смещения α вводит «ложную диссипацию», в результате чего данный метод подавляет колебания по высоким модам даже при отсутствии физического демпфирования. Если ввести параметр ωΔt, где ω – пробная частота, а Δt – выбранный шаг интегрирования, то частоты, хорошо аппроксимируемые данным шагом Δt, удовлетворяют неравенству ωΔt< 1. Частоты, для которых ωΔt> 1, при выбранном шаге Δt аппроксимируются плохо, и если вклад мод колебаний соответствующих высоких частот велик, то численное интегрирование задачи (6) будет выполнено со значительной погрешностью. Часто это приводит к тому, что реакция расчетной модели по высоким (плохо аппроксимируемым) модам искажает численное решение. В таких случаях использование метода, вводящего ложную диссипацию, часто спасает положение. Строго говоря, при α ≠ 0 α–HHT метод математически некорректен, поскольку ложное затухание проявляется также и для частот ωΔt < 1, хорошо аппроксимируемых при выбранном шаге Δt, хотя и в значительно меньшей степени, чем для плохо аппроксимируемых высоких частот. Однако для многих практических приложений малое подавление низких частот в пределах относительно небольшого количества циклов является приемлемым.
Параметр α ∈ [0, –1/3] обеспечивает устойчивое численное решение, причем наибольшее подавление высоких мод имеет место при α = –1/3. При α = 0 ложное затухание отсутствует, и α – HHT метод переходит в абсолютно устойчивый и строго корректный метод Ньюмарка.
Весь временной интервал [tstart,tend] разбивается на конечное число шагов Nstep=Tdur/Δt+1, Tdur=tend-tstart. В пределах одной постановки задачи шаг интегрирования Δt сохраняется постоянным. Если возникает необходимость интегрировать уравнения движения с разным по величине шагом, необходимо разбить весь временной интервал на подинтервалы [t0,t1], [t1,t2], ... ,[tk-1,tk], каждый из которых интегрируется с постоянным в пределах интервала шагом Δtk (рис. 3). Первая постановка задачи – начало расчета – выполняется для первого подинтервала [t0,t1], а остальные постановки задачи – продолжение расчета – соответственно для подинтервалов [t1,t2], ... ,[tk-1,tk].
Запись результатов (перемещений, скоростей, ускорений) производится в некоторые из тех моментов времени, которые совпадают с точками интегрирования (рис. 4).
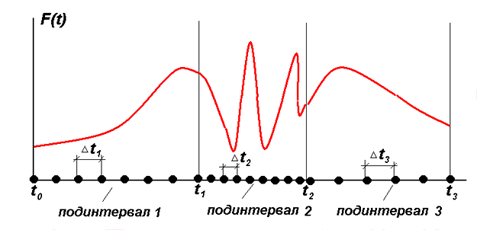
Рис. 3. Разбивка на подинтервалы
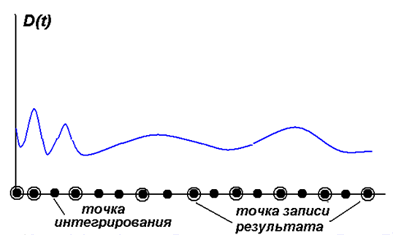
Рис. 4. Точки интегрирования и точки записи результатов
Обычно для достижения приемлемой точности решения шаг интегрирования значительно меньше шага записи результата. Возможна запись результата как с переменным шагом, так и с постоянным.
Реализация основана на технологии разреженных матриц, что позволяет значительно ускорить вычисления и сократить время анализа.