Если в системе имеются стержневые элементы, то можно определить их свободные длины, т.е. длины таких же, но шарнирно опертых стержней, у которых критическая сила Nкр совпадает с продольным усилием в стержне системы в момент потери устойчивости. Поскольку для шарнирно опертого по концам стержня длиной l по формуле Эйлера
Nкр = π2EJ / l2,
коэффициент свободной длины (отношение свободной длины к длине стержня) будет равен
μ = [(π2EJ/(Nкр l2)]1/2, |
(2) |
где EJ — жесткости стержней в главных плоскостях инерции (для пространственной задачи — по две для каждого стержня).
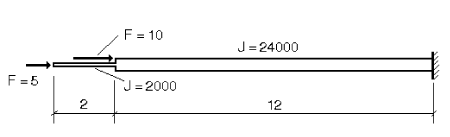
Можно проиллюстрировать сказанное примером стержня переменного сечения, сжатого силами F = 5Т и F = 10Т. Расчет этой системы дает значение k = 24,38.

Свободная длина первого элемента L1 = 25,45 м, а второго — L2 = 12,72 м. Таким образом, коэффициент свободной длины у первого элемента μ1 = 25,45/12 = 2,12, а у второго элемента — μ2 = 12,42/2 = 6,36. Подсчет по указаниям СНиП II-23-81*1 (см. приложение 6, таблица 67) дает значения
n = (2000 × 12)/(24000 × 2) = 0,5;
β = (10 + 5)/5 = 3;
α1 = (2/12) × [24000/(2000 × 3)]1/2 = 0,333.
Интерполируя по таблице 67, получим μ2 = 2,136 и μ1 = 2,136/0.333 = 6,236.
1 Здесь и далее в этой мы ссылаемся на СНиП II-23-81*, но в равной степени все написанное относится и к СП 16.13330 и ДБН B.2.6-163:2010.
Из формулы (2) видно, что, если в системе имеются сильно и слабо нагруженные стержни одинакового сечения и одинаково закрепленные по концам (например, колонны многоэтажного здания, где на верхних этажах сжатие меньше, чем на нижних), то слабо нагруженные стержни имеют значительно большие свободные длины. Этот факт давно и хорошо известен и не раз служил предметом оживленных дискуссий. В этих спорах было выявлено, что проверки прочности и устойчивости таких «слишком длинных» стержней выполняются вполне корректно, но проверка предельных гибкостей не должна выполняться с такими длинами. В нормативную документацию последний вывод, к сожалению, не попал.
Заметим, что когда реальный стержень разбит на конечные элементы, то в результате расчета выдается свободная длина каждого из этих конечных элементов. Так, в рассмотренном выше примере, если разбить первый элемент, например, на четыре равные части, то в результате расчета свободная длина каждой из них получится равной 25,45 м, и проверки любой из этих частей выполнялись бы в одинаковых условиях.