Главные и эквивалентные напряжения
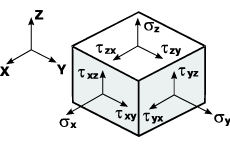
Рис. 1.
Компоненты напряжений
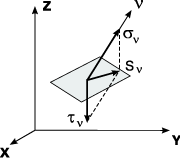
Рис. 2.
Напряжения на произвольной площадке |
Приведем некоторые основные
положения теории напряжений, излагаемые обычно в курсе теории
упругости или учебниках сопротивления материалов.
Если выделить из тела в окрестности
некой точки (рис. 1) элементарный объем в виде бесконечно
малого параллелепипеда, то действие на него окружающей среды
можно заменить напряжениями, компоненты которых действуют
на грани параллелепипеда.
В силу закона
парности касательных напряжений
| \[ \tau_{xy} =\tau_{yx} , \quad \tau_{yz} =\tau_{zy}
, \quad \tau_{zx} =\tau_{xz} . \] |
(1) |
В общем случае в точке имеется
только шесть независимых компонент напряжений, которые образуют
симметричный тензор напряжений
| \[ T_{\sigma } =\left[ {{\begin{array}{*{20}c}
{\sigma_{x} } & {\tau_{xy} } & {\tau_{xz}
} \\ {\tau_{xy} } & {\sigma_{y} } & {\tau_{yz}
} \\ {\tau_{xz} } & {\tau_{yz} } & {\sigma_{z}
} \\ \end{array} }} \right]. \] |
(2) |
На проходящей через ту же точку
произвольно ориентированной площадке, нормаль которой ν
имеет направляющие косинусы l,
m, n
с осями x, y, z, действует нормальное напряжение σν
и касательное напряжение τν (рис. 2) с равнодействующей
Sν. Проекции
этой равнодействующей на координатные оси Sνx,
Sνy, Sνz связаны
с компонентами напряжений условиями равновесия (формула Коши):
| \[ \left. {\begin{array}{l} S_{\nu x} =\sigma_{x}
l+\tau_{xy} m+\tau_{xz} n \\ S_{\nu y} =\tau_{xy}
l+\sigma_{y} m+\tau_{yz} n \\ S_{\nu z} =\tau_{xz}
l+\tau_{yz} m+\sigma_{z} n \\ \end{array}} \right\}
\] |
(3) |
|
Существуют три таких взаимно перпендикулярных площадки, на которых касательные
напряжения отсутствуют. На этих, т.н. главных
площадках, действуют главные
напряжения σ1, σ2 и σ3. При этом
имеется в виду, что σ1 ≥ σ2 ≥ σ3. Известно
также, что главные напряжения обладают экстремальными свойствами, а именно
— на любой площадке результирующее напряжение Sν
≤ σ1 и Sν
≥ σ3.
Направляющие косинусы lk,
mk и nk
нормалей главных площадок νk
определяются из решения системы уравнений:
| \[ \left\{ {\begin{array}{l} (\sigma_{x} -\sigma_{k} )l_{k}
+\tau_{xy} m_{k} +\tau_{xz} n_{k} =0; \\ \tau_{xy} l_{k} +(\sigma_{y}
-\sigma_{k} )m_{k} +\tau_{yz} n_{k} =0; \\ \tau_{xz} l_{k} +\tau_{yz}
m_{k} +(\sigma_{z} -\sigma_{k} )n_{k} =0; \\ \end{array}} \right.
\] |
(4) |
ненулевое решение которой существует при равенстве нулю ее определителя.
При этом \( l^2_k + m^2_k + n^2_k = 1 \).
Из (4) следует, что главные напряжения σk(k=1,2,3) являются
корнями кубического уравнения
| \[ det\left[ {{\begin{array}{*{20}c} {\sigma_{x} -\sigma }
& {\tau_{xy} } & {\tau_{xz} } \\ {\tau_{xy} } & {\sigma_{y}
-\sigma } & {\tau_{yz} } \\ {\tau_{xz} } & {\tau_{yz}
} & {\sigma_{z} -\sigma } \\ \end{array} }} \right]=0. \] |
(5) |
Уравнение (5) в развернутой форме имеет вид
| \[ \sigma^{3}-I_{1} (T_{\sigma } )\sigma^{2}-I_{2} (T_{\sigma
} )\sigma -I_{3} (T_{\sigma } )=0, \] |
(6) |
а его коэффициенты являются инвариантами (т.е. не зависят от выбора
системы координат). Первый инвариант \( I_{1} (T_{\sigma } )=\sigma_{x}+\sigma_{y}
+\sigma_{z} \) равен утроенному среднему напряжению (гидростатическому
давлению) σ0.
Направление главных площадок можно определить не только девятью направляющими
косинусами, а и тремя эйлеровыми углами (углом прецессии ψ, углом нутации
θ и углом чистого вращения φ). С их помощью любая площадка, первоначально
расположенная в плоскости, параллельной координатной плоскости (XOY, XOZ
или YOZ), может быть установлена в произвольное положение.
Для характеристики напряженно-деформированного состояния (НДС) используется
коэффициент Лоде-Надаи
\[ \mu_{0} =2\frac{\sigma_{2} -\sigma_{3} }{\sigma_{1} -\sigma_{3} }-1,
\]
принимающий значения μ0=1 при чистом сжатии, μ0=0
при чистом сдвиге, μ0=-1 при чистом растяжении.
В принятых обозначениях при выводе результатов расчета тензор напряжений
(2) в общем случае выглядит как
| \[ T_{\sigma } =\left[ {{\begin{array}{*{20}c} {\sigma_{x}
} & {T_{xy} } & {T_{xz} } \\ {T_{xy} } & {\sigma_{y}
} & {T_{yz} } \\ {T_{xz} } & {T_{yz} } & {\sigma_{z}
} \\ \end{array} }} \right] \] |
(7) |
Для углов Эйлера введены обозначения:
θ — ТЕТА; ψ — PSI; φ — FI.

