Наименование
Тип
Координаты
Направления осей нагрузок
Численные
характеристики
Цилиндрическая

1(11)
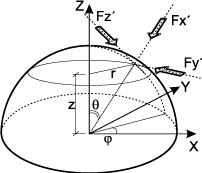
r — полярный радиус;
φ — полярный угол в радианах (градусах);
z — аппликата
X' — по радиусу от центра;
Y' — по касательной против часовой стрелки, если смотреть с конца оси Z;
Z' — совпадает с осью Z
Нет
Сферическая
и тороидальная
2(12)
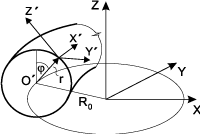
r — полярный радиус;
φ — полярный угол в радианах (градусах);
ψ — угол наклона радиуса от вертикальной оси в радианах (градусах)
X' — по радиусу от центра;
Y' — по параллели против часовой стрелки, если смотреть с конца оси Z; для тора — по окружности, параллельной плоскости XOY;
Z' — по меридиану, составляя с X' и Y' правую тройку
R0 — для тороидальной
Растяжение (сжатие) вдоль осей координат
3
Q1 Q2 Q3 — коэффициенты растяжения (сжатия) вдоль осей X, Y, Z, соответственно
Квадратичная поверхность переноса
4
X2 = X;
Y2 = Y;
Z2 = Ax2+By2+C
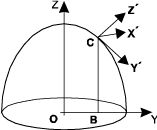
Z' — перпендикулярна поверхности и составляет с осью Z угол, меньший 90°;
Y' — перпендикулярна Z2 и лежит с осью Z в одной плоскости, составляя с осью Z угол больше 90°;
X' — перпендикулярно Y2 и Z2;
Тройка X2, Y2, Z2 — правая
Перенос координат в пространстве
5
X2 = X + A;
Y2 = Y + B;
Z2 = Z + C
A B C
Афинное преобразование
6
X2 = L11 X + L12 X + L13 X;
Y2 = L21 Y + L22 Y + L23 Y;
Z2 = L31 Z + L32 Z + L33 Z
L11 L12 L13
L21 L22 L23
L31 L32 L33
Перенос с поворотом в плоскости XOY
7(17)
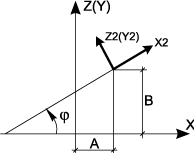
X2=X cosφ - Y sinφ + A;
Y2=X sinφ - Y cosφ + B;
Z2= Z
φ A B
Перенос с поворотом в плоскости XOZ
8(18)
X2 = X cosφ - Z sinφ + A;
Y2 = Y;
Z2 = X sinφ + Z cosφ + B
φ A B
9
X2 = X;
Y2 = Y;
\[ Z=\sqrt{A \cdot x^2 + B \cdot y^2 + C} \]
A B C
Поверхность переноса
10
X2 = X;
Y2 = Y;
\[ Z=\sqrt{A \cdot x + B \cdot y + C} \]
A B C