General Information

Thin-walled bars can be found in a great variety of structures used in various fields of engineering. In some cases a thin-walled bar model describes a structure as a whole (such as a multi-storey building with load-bearing walls or a span of a bridge), while in other cases this model can be used to describe important load-bearing components of a framework.

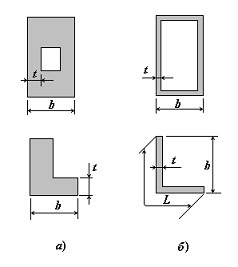
In structural mechanics, a bar refers to a body with the maximal overall cross-sectional dimension b_max much smaller than the length l.

The minimal cross-sectional dimension of a solid bar, t_min, has the same order of magnitude as b_max (Fig.1, a). For thin-walled bars, t_min << b_max so, obviously, t_min << L, where L is the length of the cross-section contour of the bar [2] (Fig.1, b). A bar is usually considered to be thin-walled if the following inequalities hold:  

t  /  b  <  0,1; b  /  l  <  0,1.

Figure 1

A key difference in the behavior of a thin-walled bar under a load from that of a solid bar is that the plane-sections hypothesis can be violated in the case of the thin-walled bar. A typical example is a free torsion of an open-profile bar (a pipe with a longitudinal cut) or a deformation of an I-beam loaded by a bimoment at its end (Fig. 2). A deviation from the plane-sections hypothesis is a feature more immanent to open-profile thin-walled bars than to closed-profile ones.

A theory for analysis of open- and closed-profile bars of this type was developed by V.Z. Vlasov [3] and A.A.Umanski [4],[5] (see also [6]).

Tonus enables you to consider any arbitrary (including mixed open-close) profile. It uses a modification of a unified thin-walled bar theory suggested by E.A. Beilin [7]. Unlike Section Builder and Consul, this software implements a different approach to the creation of a cross-section model. The application assumes that a section is thin-walled and is being built of strips; the user specifies the thickness of each strip and the position of its centerline.

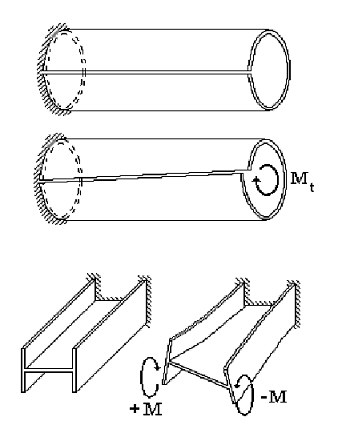
Figure 2

For the designed section Tonus determines:

• cross-sectional area А;
• values of the moments of inertia I_y and I_z about centroidal axes parallel to the coordinate axes;
• radii of gyration i_y  and i_z about the same axes;
• torsional moment of inertia I_t;
• coordinates of the center of mass;

• value of the angle of the principal axes of inertia (angle α between U and Y axes);
• maximum I_u and minimum I_v moments of inertia;
• maximum i_u and minimum i_v radii of inertia;
• maximum W_u+ and minimum W_u- section moduli about the U axis;
• maximum W_v+ and minimum W_v- section moduli about the V axis;
• core size from U axis along the positive (а_u+) and negative (а_u-) directions of the V axis;
• core size from V axis along the positive (a_v+) and negative (a_v-) directions of the U axis;
• section perimeters: total P, external P_e and internal P_i;
• conventional shear areas (A_v,y, A_v,z);
• moments of inertia with respect to the coordinate system within which the section has been created;
• coordinates of the shear center;
• sectorial moment of inertia.

The geometric properties are always calculated considering the section as continuous, neglecting the ductility of connecting grates and/or plates.

It should be noted that in case of a section with equal moments of inertia (I_y = I_z) the angle α is undefined. The axes shown on the screen are to some extent accidental, since in the considered case the ellipse of inertia degenerates into a circle of inertia (i_y = i_z = i_u = i_v), so any orthogonal couple of central axes can be considered as the principal one.

The calculation of geometric properties is not a goal by itself. It is assumed, that the calculation results will be used during the further analysis of the stress-strained state, in particular, when specifying the initial data in any program of the structural calculation. Moreover, the program can be used to calculate the stiffness properties of buildings and structures and their elements. Tonus enables to obtain the fields of normal stresses if the internal forces in the section have been specified.