Назначение

Тонкостенные стержни входят в состав самых разнообразных инженерных сооружений, относящихся к различным областям техники. В некоторых случаях такая расчетная модель описывает сооружение в целом (например многоэтажное здание с несущими стенами или пролетное строение моста), в других случаях — важные несущие компоненты силового каркаса.

В строительной механике стержнем называется тело, у которого максимальный габаритный размер поперечного сечения b_max намного меньше его длины l.

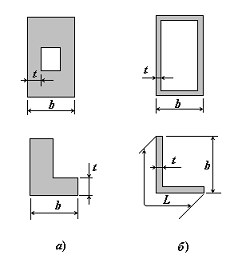
В массивных стержнях наименьший размер поперечного сечения t_min имеет одинаковый с b_max порядок величины (рис.1, а). В тонкостенном стержне t_min << b_max и, разумеется, t_min << L, где L — длина контурной линии поперечного сечения тонкостенного стержня [2] (рис.1, б). Обычно стержень считают тонкостенным, если выполняются неравенства:

t / b < 0,1; b / l < 0,1.

Рис. 1

Основное отличие в поведении тонкостенного стержня под нагрузкой от работы массивного стержня состоит в возможном нарушении гипотезы плоских сечений. Типичным примером может служить свободное кручение стержня открытого профиля (труба с продольным разрезом) или же деформация двутавра, загруженного на торце бимоментом (рис. 2). Отклонение от гипотезы плоских сечений (депланация) в большей мере характерна для тонкостенных стержней открытого профиля и в меньшей — для тонкостенных стержней замкнутого профиля.

Теория расчета стержней подобного вида для случаев открытого и замкнутого профилей развита в работах В.З.Власова [3] и А.А.Уманского [4],[5] (см. также [6]).

Программа Тонус позволяет рассматривать произвольные (в том числе открыто-замкнутые) профили; при этом используется вариант единой теории тонкостенных стержней, предложенный Е.А.Бейлиным [7]. В отличии от программ Конструктор Сечений и Консул, здесь реализован другой подход к формированию модели поперечного сечения. Предполагается, что сечение является тонкостенным и формируется из полосок заданием их толщины и определением положения их срединной линии.

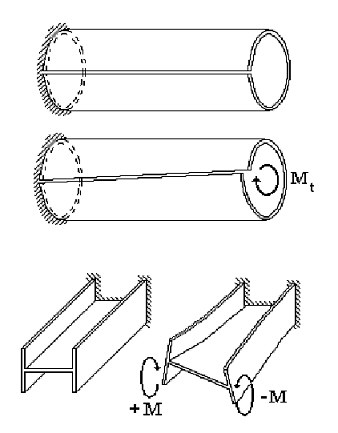
Рис. 2

Для сконструированного сечения Тонус определяет:

• площадь поперечного сечения А;
• значения моментов инерции I_y и I_z относительно центральных осей, параллельных координатным осям;
• радиусы инерции i_y и i_z относительно тех же осей;
• момент инерции при свободном кручении I_t;
• координаты центра масс;
• значение угла наклона главных центральных осей инерции (угол a между осями U и Y);
• максимальный I_u и минимальный I_v моменты инерции;
• максимальный i_u и минимальный i_v радиусы инерции;
• максимальный W_u+ и минимальный W_u- моменты сопротивления относительно оси U;
• максимальный W_v+ и минимальный W_v- моменты сопротивления относительно оси V;
• ядровое расстояние от оси U, отсчитываемое вдоль положительного (а_u+) и отрицательного (а_u-) направления оси V;
• ядровое расстояние от оси V, отсчитываемое вдоль положительного (a_v+) и отрицательного (a_v-) направления оси U;
• периметры сечения: полный — P, внешний — P_e и внутренний — P_i;
• условные площади среза (A_v,y, A_v,z);
• моменты инерции относительно системы координат, в которой создавалось сечение;
• координаты центра изгиба;
• секториальный момент инерции.

Геометрические характеристики всегда вычисляются как для сплошностенчатого сечения — податливость соединительных решеток и/или планок не учитывается.

Необходимо отметить, что в случае сечений с равными моментами инерции (I_y = I_z) угол a является неопределенным и, показываемые на экране оси, являются, в какой-то мере, случайными. Эллипс инерции вырождается в круг инерции (i_y = i_z = i_u = i_v), и любая ортогональная пара центральных осей может быть названа главной.

Вычисление геометрических характеристик не является самоцелью. Предполагается, что результаты расчета будут использованы при дальнейшем исследовании напряженно-деформированного состояния, в частности, при задании исходных данных в любой программе прочностного расчета. Кроме того, программа может быть использована для определения жесткостных характеристик зданий и сооружений и их элементов. Сама программа Тонус позволяет получить поля нормальных напряжений, если заданы внутренние усилия в сечении.