Analysis of a Reinforced Concrete Foundation Slab for Normal Crack Opening

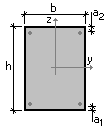
Figure 1. Design cross-section of the element

Objective: Check the calculation of the crack opening width.        

Task: Verify the correctness of the analysis of normal crack opening.

References:

1. Guide on designing of concrete and reinforced concrete structures made of heavy-weight concrete (no prestressing) (to SP 52-101-2003), 2005, p. 155-157.

2. M.A. Perelmuter, K.V. Popok, L.N. Skoruk, Calculation of the Normal Crack Opening Width for SP 63.13330.2012, Concrete and Reinforced Concrete, 2014, №1, p.21,22

Initial data file:

Example 43.SAV
report – Arbat 43.doc

Compliance with the codes: SP 52-101-2003, SP 63.13330.2012. 

Initial data:

b×h = 1150×300 mm	Slab section sizes
а = 42 mm	Distance from the center of gravity of the reinforcement to he compressed edge of the section
As = 923 mm2 (6Ø14)	Cross-sectional area of reinforcement
Ml = 50 kH∙m	Moment in the design section from permanent and long-term loads
Msh = 10 kH∙m	Moment from short-term loads
Concrete class Class of reinforcement	В15 А400

 

ARBAT initial data:

Importance factor  γ_n = 1
Importance factor (serviceability limit state)  = 1
Member length 1 m
Effective length factor in the XoY plane 1
Effective length factor in the XoZ plane 1
Random eccentricity along Z according to SNiP 52-01-2003 (Russia)
Random eccentricity along Y according to SNiP 52-01-2003 (Russia)
Structure is statically indeterminate
Limit slenderness - 200

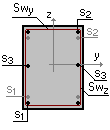
Section:

b = 1150 mm h = 300 mm a1 = 35 mm a2 = 35 mm	S1 - 6Ø14

 

Reinforcement	Class	Service factor
Longitudinal	A400	1
Transverse	A240	1

 

Concrete:
Concrete type: Heavy-weight
Concrete class: B15

Service factor for concrete
γb1	allowance for the sustained loads	1
γb2	allowance for the failure behavior	1
γb3	allowance for the vertical position during concreting	1
γb4	allowance for the freezing/thawing and negative temperatures	1

Humidity of environmental air - 40-75%

Crack resistance:

Limited crack opening width
Requirements to crack opening width are based on the preservation of reinforcement
Allowable crack opening width:
  Short-term opening  0,4 mm
  Long-term opening  0,3 mm

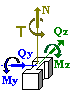
Forces:

N = 0 kN
M_y = 60 kN*m
Q_z = 0 kN
M_z = 0 kN*m
Q_y = 0 kN
T = 0 kN*m
Factor for sustained load 0,83333

Theoretical solution:

Diagrams of the strain ε and stress σ distribution in concrete for the determination of the stress σ_s obtained in the theoretical calculation [2] based on the nonlinear deformation model are shown in Fig. 2. The following values of the internal longitudinal force N and bending moment M correspond to these diagrams

N = 0,00439 kN ≈ 0;
M = 50,096 ≈ 50 kNm.

There is a balance between internal and external forces. In this solution the stress in the tensile reinforcement is σ_s=236,692 MPa.

Figure 2. Strain e and stress s diagrams (for the determination of σ_s)

 

Similarly, solving the problem of determining the cracking moment, we obtain the following diagrams (Fig. 3), which satisfy the requirements of Sec. 8.2.14 of SP 63.13330.2012.

Figure 3. Strain e and stress s diagrams (for the determination of σ_s,crc)

 

In accordance with these diagrams M_crc= 36,244 kN∙m, σ_s,crc =  22,651 MPa.

On the basis of formula (1) (formula (8.128) SP 63.13330.2012) we obtain a_crc=0,306 mm.

\[ a_{crc} =\varphi_{1} \cdot \varphi_{2} \cdot \varphi_{3} \cdot \psi_{s} \cdot \frac{\sigma_{s} }{E_{s} }\cdot l_{s} . \]

(1)

Comparison of solutions:

Check	crack opening width (long-term)
Theory	0,306/0,3 = 1,02
ARBAT	0,974
Deviation, %	4,51%

 

Comments:

1. The member length and the class of transverse reinforcement have to be specified in ARBAT. Since they are not determined in the problem, the following data are used 1 m and А240, respectively.
2. The value of the concrete cover is equal to a – d/2 = 42 – 14/2 = 35 mm.
3. The value of the total moment acting in the section, М = M_l + M_sh = 50 + 10 = 60 kN∙m, factor for sustained load is equal to M_l /М = 50/60 = 0,833.
4. The crack opening width obtained in the Guide [1] is equal to 0.227 mm. Such a significant discrepancy with the above theoretical solution is due to the use of the approach based on the ultimate forces, instead of the nonlinear deformation model (see [2]).
5. The deviation of the results of ARBAT from the theoretical solution is due to the fact that in order to provide computational stability, diagrams in which the horizontal part of the graph σ(ε) has a small slope are used in ARBAT instead of the perfect diagrams of the material behavior.