Punching Analysis of a Flat Monolithic Floor Slab

1 – force application point N; 2 – center of gravity of the open contour; 3 – open contour of the design section

Objective: Check the Punching mode.

Task: Verify the correctness of the punching strength analysis of a concrete element under a concentrated force and a bending moment when the load application area is near the edge of the slab.

References: Guide on designing of concrete and reinforced concrete structures made of heavy-weight concrete (no prestressing) (to SP 52-101-2003), 2005, p. 140-142.

Initial data file:

Example 41.SAV;
report:
when the analysis is performed according to SNiP 52-01-2003 – Arbat 41.1.doc,
when the analysis is performed according to SP 63.13330.2012 – Arbat 41.2.doc.

Compliance with the codes: SNiP 52-101-2003, SP 63.13330.2012.

Initial data from the source:

h = 230 mm	Slab thickness
a×b = 500×400 mm	Column section sizes
N = 150 kN∙m	Load transferred from the floor slab to the column
M_sup = 80 kN∙m	Moment in the column section on the upper face of the slab
M_inf = 90 kN∙m	Moment in the column section on the lower face of the slab
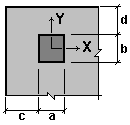
x₀= 500 mm	Distance from the center of the column section to the free edge of the slab
Concrete class	В25

ARBAT initial data:

Importance factor γ_n= 1
Load application area is near the free edge of the element

a = 0,5 m
b = 0,4 m
c = 0,25 m
d = 4 m
Effective height of the section for longitudinal reinforcement
along X-axis - 0,2 m
along Y-axis - 0,2 m

Concrete:

Concrete type: Heavy-weight

Concrete class: B25

Service factor for concrete
γ_b1	allowance for the sustained loads	1
γ_b2	allowance for the failure behavior	1
γ_b3	allowance for the vertical position during concreting	1
γ_b4	allowance for the freezing/thawing and negative temperatures	1

Loads:

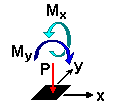
	P	M_x	M_y
	kN	kN*m	kN*m
1	150	0	170

Forces:
P = 150 kN
M_x = 0 kN*m
M_y = 170 kN*m

Comparison of solutions (according to SP 52-101-2003):

Report file	Arbat 41.1.doc
Check	punching strength of a concrete element under a concentrated force and bending moments with their vectors along X and Y axes	punching strength of an unclosed concrete element under a concentrated force and bending moments (including additional ones caused by the eccentric application of a force with respect to the punched contour) with their vectors along X,Y-axes (load application area is near the edge of the slab)
Guide	203,4/210 = 0,969	202,2/210 = 0,963
ARBAT	0,549	0,621
Deviation, %	43,4%	35,5%
Analytical solution (see below)	0,550	0,622
Deviation, %	0,1 %	0,1 %

Comparison of solutions (according to SP 63.13330.2012):

Report file	Arbat 41.2.doc
Check	punching strength of a concrete element under a concentrated force and bending moments with their vectors along X and Y axes	punching strength of an unclosed concrete element under a concentrated force and bending moments (including additional ones caused by the eccentric application of a force with respect to the punched contour) with their vectors along X,Y-axes (load application area is near the edge of the slab)
ARBAT	0,413	0,466
Analytical solution (see below)	0,412	0,466
Deviation, %	0,1 %	0 %

Comments:

The average effective height of the slab is taken as h₀ = 200 mm in the calculation of the problem in the Guide. This value is used in ARBAT.
The value of the sum of moments M_sup and M_inf on the upper and lower faces of the slab is used in ARBAT. Thus, M = 80 + 90 = 170 kN∙m.
Distance from the edge of the load application area to the free edge of the slab с is equal to the difference between the distance from the center of the column section to the free edge of the slab and half the size of the column section in this direction: с = x₀ – а/2 = 0,5 – 0,5/2 = = 0,25 m.
In order to analyze the case when the (column) load transfer area is located near the edge of the flat element (floor slab), in ARBAT one of the values of the distance from the edge of the load application area to the free edge of the slab has to be greater than three times the effective height of the slab. Thus, d = 4 m > 3h₀ = 0,6 m.
Such significant differences in the obtained factors with the solution from the Guide are due to the following reasons:
- it is indicated in the codes that the calculations use the smallest values of the section moduli W_bx, determined from the following formulas:
  \[ \mbox{W}_{bx} =\frac{\mbox{I}_{bx} }{\mbox{x}_{0} } \quad and \quad \mbox{W}_{bx} =\frac{\mbox{I}_{bx} }{\mbox{L}_{x} \mbox{-x}_{0} }. \]
  In this problem the smaller value is the one determined by the first formula, since х₀ = 0,5 + 0,0359 = 0,5359 m > Lx – х₀ = 0,85 – 0,5359 = 0,3141 m (where х₀ is the position of the center of gravity of the design open contour in the direction of the Х axis). Thus, the value W_bx determined by the first formula is used in ARBAT. While the value determined by the second formula is used in the Guide;
- the check of the strength requirements in the Guide does not take into account the recommendations of the codes according to which under the action of concentrated moments and a force the ratio between the acting concentrated moments М, taken into account at punching, and the ultimate ones M_ult should be taken not greater than the ratio between the acting concentrated force F and the ultimate one F_ult (Sec. 6.2.46 of SNiP 52-101-2003) and not greater than half the ratio between the acting concentrated force F and the ultimate one F_ult(Sec. 8.1.46 of SP 63.13330.2012).
The analytical solution is given below.

Analytical solution

1 – closed design contour №1, 2 – open design contour №2, 3 – open design contour №3.

In this case it is necessary to check the strength of three contours of the design cross-section:

contour №1 – closed contour around the column section at a distance of 0,5h₀ from the column contour;

contour №2 – open contour around the column section at a distance of 0,5h₀ from the column contour with the extension of the contour to the free edge of the slab;

contour №3 – open contour around the column section at a distance of 0,5h₀ from the column contour (contour of the verification analysis without the consideration of the reinforcement).

Closed contour №1:

L_x = A_x + h₀ = 500 + 200 = 700 mm = 0,7 m,

L_y = A_y + h₀ = = 400 + 200 = 600 mm = 0,6 m,

Perimeter of the design contour of the cross-section:

u = 2(L_x = L_y) = 2 (0,7 + 0,6) = 2,6 m.

Area of the design contour of the cross-section:

A_b = uh₀ = 2,6 × 0,2 = 0,52 m²

Ultimate force resisted by concrete:

F_b,ult = R_btA_b = 1,05 × 10³ × 0,52 = 546 kN.

Moment of inertia of the design contour with respect to the X axis passing through its center of gravity:

\[ I_{bx} =2\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}= \quad 2\frac{0,6^{3} }{12}+2\cdot 0,7\left( {\frac{0,6}{2}} \right)^{2}=\quad 0,162 \quad m^{3}. \]

Section modulus of the design contour of concrete:

\[ W_{bx} =\frac{I_{bx} }{y_{\max } }= \quad \frac{0,162}{0,3}=\quad 0,54 \quad m^{2}. \]

Moment of inertia of the design contour with respect to the Y axis passing through its center of gravity:

\[ I_{by} =2\frac{L_{x}^{3} }{12}+2\cdot L_{y} \left( {\frac{L_{x} }{2}} \right)^{2}= \quad 2\frac{0,7^{3} }{12}+2\cdot 0,6\left( {\frac{0,7}{2}} \right)^{2}=\quad 0,204 \quad m^{3}. \]

Section modulus of the design contour of concrete:

\[ W_{by} =\frac{I_{by} }{x_{\max } }= \quad \frac{0,204}{0,35}=\quad 0,583 \quad m^{2}. \]

Bending moment which can be resisted by concrete in the design cross-section:

M_bx,ult= R_btW_bxh₀ = 1,05 × 10³ × 0,54 × 0,2 = 113,4 kNm.

M_by,ult= R_btW_byh₀ = 1,05 × 10³ × 0,583 × 0,2 = 122,4 kNm.

For SNiP 52-101-2003:

\[ \frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} }; \quad \frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{85}{122,4}=0,694\le \frac{F}{F_{b,ult} }=\frac{150}{546}=0,275 \) – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,275 \]

Punching strength of the slab:

\[ K_{1} =\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \]

\[ K_{1} = 0,275 + 0 + 0,275 = 0,55 \]

For SP 63.13330.2012:

\[ \frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 0,5\frac{F}{F_{b,ult} } \]

\( \frac{M_{y} }{M_{by,ult} }=\frac{85}{122,4}=0,694\le 0,5\frac{F}{F_{b,ult} }=\frac{150}{546}=0,5\cdot 0,275=0,1375 \) – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,1375 \]

Punching strength of the slab:

\[ K_{1} =\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \]

\[ K_{1} = 0,275 + 0 + 0,1375 = 0,413\]

Open contour №2:

L_x = A_x +h₀ + 150 = 500 + 200 + 150 = 850 mm = 0,85 m,

L_y = A_y +h₀= 400 + 200 = 600 mm = 0,6 m,

Perimeter of the design contour of the cross-section:

u = 2L_x +L_y = 2 × 0,85 + 0,6 = 2,3 m.

Area of the design contour of the cross-section:

A_b = uh₀2,3 × 0,2 = 0,46 m².

X coordinate of the center of gravity of the open contour with respect to the left edge of the slab:

\[ X=\frac{425\cdot 850\cdot 2+850\cdot 600}{850\cdot 2+600}=535,869 mm \]

Ultimate force resisted by concrete:

F_b,ult = R_btA_b =1,05 × 10³ × 0,46 = 483 кН.

Moment of inertia of the design contour with respect to the X axis passing through its center of gravity:

\[ I_{bx} =\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}= \quad \frac{0,6^{3} }{12}+2\cdot 0,85\left( {\frac{0,6}{2}} \right)^{2}=\quad 0,171 \quad m^{3}. \]

Section modulus of the design contour of concrete:

\[ W_{bx} =\frac{I_{bx} }{y_{\max } }= \quad \frac{0,171}{0,3}=\quad 0,57 \quad m^{2}. \]

Moment of inertia of the design contour with respect to the Y axis passing through its center of gravity:

\[ I_{by} =2\frac{L_{x}^{3} }{12}+2L_{x} (0,075+0,035869)^{2}+L_{y} \left( {0,35-0,035869} \right)^{2}= 2\frac{0,85^{3} }{12}+2\cdot 0,85(0,075+0,035869)^{2}+0,6\left( {0,35-0,035869} \right)^{2}=0,183 \quad m^{3}. \]

Section modulus of the design contour of concrete:

\[ W_{by} =\frac{I_{by} }{x_{\max } }= \frac{0,183}{0,535869}= 0,341 \quad m^{2}. \]

Bending moment which can be resisted by concrete in the design cross-section:

M_bx,ult = R_btW_bxh₀= 1,05 × 10³ × 0,57 × 0,2 = 119,7 kNm.

M_by,ult = R_btW_byh₀= 1,05 × 10³ × 0,341 × 0,2 = 71,6 kNm.

M_y = M_y - Fe₀= 85 – 150 × 0,035869 = 85 – 5,38 = 79,62 kNm.

For SNiP 52-101-2003:

\[ \frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} }; \quad \frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} } \]

\( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le \frac{F}{F_{b,ult} }=\frac{150}{483}=0,311 \) – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,311 \]

Punching strength of the slab:

\[ K_{1} =\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ K_{1} \quad = \quad 0,311+0+0,311 = 0,622 \]

For SP 63.13330.2012:

\[ \frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 0,5\frac{F}{F_{b,ult} } \]

\( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le 0,5\frac{F}{F_{b,ult} }=\frac{150}{483}=0,5\cdot 0,311=0,155 \) – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,155 \]

Punching strength of the slab:

\[ K_{1} =\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ K_{1} \quad = 0,311 + 0 + 0,155 = 0,466 \]

Open contour №3:

L_x = A_x + 2 × 1,5h₀ = 500 + 1,5 × 200 + 250 = 1050 мм = 1,05 m,

L_y = A_y + 2 × 1,5h₀ = 400 + 2 × 1,5 × 200 = 1000 мм = 1,0 m,

Perimeter of the design contour of the cross-section:

u = 2L_x + L_y = 2 × 1,05 + 1,0 = 3,1 m.

Area of the design contour of the cross-section:

A_b = uh₀ = 3,1 × 0,2 = 0,62 m².

X coordinate of the center of gravity of the open contour with respect to the left edge of the slab:

\[ X=\frac{525\cdot 1050\cdot 2+1050\cdot 1000}{1050\cdot 2+1000}=694,355 \quad mm \]

Ultimate force resisted by concrete:

F_b,ult = R_btA_b = 1,05 × 10³ × 0,62 = 651 kN.

Moment of inertia of the design contour with respect to the X axis passing through its center of gravity:

\[ I_{bx} =\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}= \quad \frac{1,05^{3} }{12}+2\cdot 1,05\left( {\frac{1,0}{2}} \right)^{2}=\quad 0,608 \quad m^{3}. \]

Section modulus of the design contour of concrete:

\[ W_{bx} =\frac{I_{bx} }{y_{\max } }= \quad \frac{0,608}{0,5}=\quad 1,217 \quad m^{2}. \]

Moment of inertia of the design contour with respect to the Y axis passing through its center of gravity:

\[ I_{by} =2\frac{L_{x}^{3} }{12}+2L_{x} (0,194355-0,025)^{2}+L_{y} \left( {1,05-0,694355} \right)^{2}= 2\frac{1,05^{3} }{12}+2\cdot 1,05(0,194355-0,025)^{2}+1,0\left( {1,05-0,694355} \right)^{2}=0,38 \quad m^{3}. \]

Section modulus of the design contour of concrete:

\[ W_{by} =\frac{I_{by} }{x_{\max } }= \quad \frac{0,38}{0,694355}=\quad 0,547 \quad m^{2}. \]

Bending moment which can be resisted by concrete in the design cross-section:

M_bx,ult = R_btW_bxh₀= 1,05 × 10³ × 1,217 × 0,2 = 255,57 kNm.

M_by,ult = R_btW_byh₀=1,05 × 10³ × 0,547 × 0,2 = 114,87 kNm.

M_y = M_y – Fe₀=85 – 150 × 0,194355 = 85 – 29,15 = 55,85 kNm.

For SNiP 52-101-2003:

\[ \frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} }; \quad \frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} } \]

\( \frac{M_{y} }{M_{by,ult} }=\frac{55,85}{114,87}=0,486\le \frac{F}{F_{b,ult} }=\frac{150}{651}=0,23 \) – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,23 \]

Punching strength of the slab:

\[ K_{1} =\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ K_{1} \quad = 0,23 + 0 + 0,23 = 0,46 \]

For SP 63.13330.2012:

\[ \frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 0,5\frac{F}{F_{b,ult} } \]

\( \frac{M_{y} }{M_{by,ult} }=\frac{55,85}{114,87}=0,486\le 0,5\frac{F}{F_{b,ult} }=\frac{150}{651}=0,5\cdot 0,23=0,115 \) – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,155 \]

Punching strength of the slab:

\[ K_{1} =\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ K_{1} \quad = 0,23 + 0 + 0,115 = 0,345 \]