Punching Analysis of a Reinforced Concrete Floor Slab

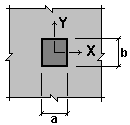
Figure 1. To the example of the calculation 40
1 - 1-st design section, 2 - 2-nd design section

Objective: Check the Punching mode.

Task: Verify the correctness of the punching strength analysis of a concrete element with transverse reinforcement under a concentrated force and bending moments and punching strength analysis beyond the boundary of transverse reinforcement.

References: Guide on designing of concrete and reinforced concrete structures made of heavy-weight concrete (no prestressing) (to SP 52-101-2003), 2005, p. 137-140.

Initial data file:

Пример 40.SAV
report – Arbat 40.doc

Compliance with the codes: SP 52-101-2003, SP 63.13330.2012. 

Initial data from the source:

The same in the direction of the Y axis

h = 220 mm	Slab thickness
a×b = 500×800 mm	Column section sizes
N = 800 kN	Load transferred from the floor slab to the column
Mx,sup = 70 kN∙m	Moment in the column section on the upper face of the slab in the direction of the X axis
My,sup = 30 kN∙m
Mx,inf = 60 kN∙m	Moment in the column section on the lower face of the slab in the direction of the X axis
My,inf = 27 kN∙m	The same in the direction of the Y axis
d = 6 mm	Diameter of transverse reinforcement
Concrete class Class of reinforcement	В30 А240

 

ARBAT initial data:

Importance factor γ_n = 1
Load application area is inside the element

a = 500 mm b = 800 mm Effective height of the section for longitudinal reinforcement      along X-axis - 190 mm      along Y-axis - 190 mm

Concrete:

Concrete type: Heavy-weight
Concrete class: B30

Service factor for concrete
γb1	allowance for the sustained loads	1
γb2	allowance for the failure behavior	1
γb3	allowance for the vertical position during concreting	1
γb4	allowance for the freezing/thawing and negative temperatures	1

 

Loads:

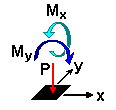
	P	Mx	My
	kN	kN*m	kN*m
1	800	57	130

Uniform reinforcement:

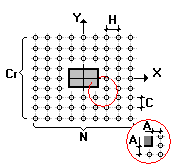
Class of reinforcement: A240
Diameter 6 mm

Distance to the load application area 75 mm
Spacing of rebars in a row 60 mm
Number of rebars in a row 20
Spacing of rows 60 mm
Number of rows of rebars 25

Forces:

P = 800 kN
M_x = 57 kN*m
M_y = 130 kN*m

Comparison of solutions:

Check	punching strength of a concrete element with transverse reinforcement under a concentrated force and bending moments with their vectors along X and Y axes	punching strength of a concrete element with transverse reinforcement under a concentrated force beyond the boundary of transverse reinforcement
Guide	343,5/347,7 = 0,988	146,5/218,5 = 0,67
ARBAT	0,973	0,75
Deviation, %	1,518%	10,667%

 

Comments:

1. The average effective height of the slab is taken as h₀ = 190 mm in the calculation of the problem in the Guide. This value is used in ARBAT.
2.  In the Guide moments M_x and M_y are moments in the directions of X and Y axes respectively. In ARBAT moments M_x and M_y are moments about Х and Y axes respectively, therefore moments M_x and M_y in the example of the Guide correspond to the moments M_y and M_x in ARBAT. The values of the sum of moments M_sup and M_inf on the upper and lower faces of the slab are used in ARBAT. Thus, M_x = 30 + 27 = 57 kN∙m, M_y = 70 + 60 = 130 kN∙m.
3. The number of rebars in a row 20 and the number of rows of rebars 25 are taken in accordance with the sizes given in the drawing in the Guide.
4. The difference between the second factor and the solution from the Guide is due to the following reasons:

• in the problem the boundaries of the second design contour are considered at the distance of 0,5h₀ from the boundary of the specified transverse reinforcement. Moreover, in the calculation of the geometric properties in the Guide the sizes of the contour were incorrectly taken as greater by 0,5h₀ than the sizes of the considered contour. In ARBAT the boundaries of the second design contour were taken at the distance of 0,5h₀ from the boundary of the transverse reinforcement considered in the calculation;
• in the Guide this strength check is performed taking into account the bending moments. In ARBAT the check is performed according to Sec.6.2.48 of SP 52-101-2003 by the formula for the punching analysis under the action of a concentrated force.