Расчет железобетонной плиты фундамента по раскрытию нормальных трещин
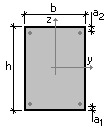
Рис. 1. Расчетное сечение элемента
Цель: Проверка расчета ширины раскрытия трещин.
Задача: Проверить правильность анализа раскрытия нормальных трещин.
Ссылки:
1. Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101-2003), 2005, с. 155-157.
2. М.А. Перельмутер, К.В. Попок, Л.Н. Скорук, Расчет ширины раскрытия нормальных трещин по СП 63.13330.2012, Бетон и железобетон , 2014, №1, с.21,22
Файл с исходными данными:
Example 43.SAV
отчет – Arbat 43.doc.
Соответствие нормативным документам: СП 52-101-2003, СП 63.13330.2012.
Исходные данные:
| b×h = 1150×300 мм | Размеры сечения плиты |
| а = 42 мм | Расстояние от центра тяжести арматуры до сжатого края сечения |
| As = 923 мм2 (6Ø14) | Площадь сечения арматуры |
| Ml = 50 кН∙м | Момент в расчетном сечении от постоянных и длительных нагрузок |
| Msh = 10 кН∙м | Момент от кратковременных нагрузок |
|
Класс бетона В15 |
Исходные данные АРБАТ:
Коэффициент надежности по ответственности γn = 1
Коэффициент надежности по ответственности (2-е предельное состояние) = 1
Длина элемента 1 м
Коэффициент расчетной длины в плоскости XoY 1
Коэффициент расчетной длины в плоскости XoZ 1
Случайный эксцентриситет по Z принят по СНиП 52-01-2003 (Россия)
Случайный эксцентриситет по Y принят по СНиП 52-01-2003 (Россия)
Конструкция статически неопределимая
Предельная гибкость - 200
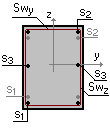
Сечение
|
b = 1150 мм
|
S1 - 6Ø14
|
|
Арматура |
Класс |
Коэффициент условий работы |
|
Продольная |
A400 |
1 |
|
Поперечная |
A240 |
1 |
Бетон
Вид бетона: Тяжелый
Класс бетона: B15
|
Коэффициенты условий работы бетона |
||
|---|---|---|
|
γb1 |
учет нагрузок длительного действия |
1 |
|
γb2 |
учет характера разрушения |
1 |
|
γb3 |
учет вертикального положения при бетонировании |
1 |
|
γb4 |
учет замораживания/оттаивания и отрицательных температур |
1 |
Влажность воздуха окружающей среды - 40-75%
Трещиностойкость
Ограниченная ширина раскрытия трещин
Требования к ширине раскрытия трещин выбираются из условия сохранности арматуры
Допустимая ширина раскрытия трещин:
Непродолжительное раскрытие 0,4 мм
Продолжительное раскрытие 0,3 мм
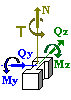
Усилия
N = 0 кН
My = 60 кН*м
Qz = 0 кН
Mz = 0 кН*м
Qy = 0 кН
T = 0 кН*м
Коэффициент длительной части 0,83333
Теоретическое решение:
При теоретическом расчете [2] по нелинейной деформационной модели при определении напряжения σs получено эпюры распределения деформаций ε и напряжений σ в бетоне, показанные на рис. 2. Этим эпюрам соответствуют следующие значения внутренней продольной силы N и изгибающего момента M
N = 0,00439 кН ≈ 0;
M = 50,096 ≈ 50 кНм.
Имеет место равновесие между внутренними и внешними усилиями. При этом решении напряжение в растянутой арматуре σs=236,692 МПа.
Рис. 2. Эпюры деформаций ε и напряжений σ (для определения σs)
Аналогично, решая задачу об определении момента трещинообразования, мы получим следующие эпюры (рис. 3), которые удовлетворяют требованиям п. 8.2.14 СП 63.13330.2012.
Рис. 3. Эпюры деформаций ε и напряжений σ (для определения σs,crc)
В соответствии с этими эпюрами Mcrc= 36,244 кН∙м, σs,скс = 22,651 МПа.
На основании формулы (1) (формулы (8.128) СП 63.13330.2012) мы получаем acrc=0,306 мм.
\[ a_{crc} =\varphi_{1} \cdot \varphi_{2} \cdot \varphi_{3} \cdot \psi_{s} \cdot \frac{\sigma_{s} }{E_{s} }\cdot l_{s} . \]
Сравнение решений
|
Проверка |
ширина раскрытия трещин (длительная) |
|
Теория |
0,306/0,3 = 1,02 |
|
АРБАТ |
0,974 |
|
Отклонение, % |
4,51% |
Комментарии
- В АРБАТ необходимо ввести длину элемента и класс поперечной арматуры. Т.к. в задаче они не определены, использованы данные соответственно 1 м и А240.
- Значение защитного слоя равно a – d/2 = 42 – 14/2 = 35 мм.
- Значение полного момента, действующего в сечении, М = Ml + Msh = 50 + 10 = 60 кН∙м, коэффициент длительной части равен Ml /М = 50/60 = 0,833.
- В Пособии [1] получена ширина раскрытия трещин, равная 0.227 мм. Столь значительное расхождение с приведенным теоретическим решением объясняется использованием подхода, основанного на предельных усилиях, вместо нелинейной деформационной модели (см. [2]).
- Отклонение результатов АРБАТ от теоретического решения связано с тем, что в АРБАТ для обеспечения вычислительной устойчивости рассматриваются не идеальные диаграммы работы материалов, а диаграммы, в которых горизонтальная часть графика σ(ε) имеет небольшой наклон.