Geometric Properties of a Square

Aim: To check the accuracy of the geometric properties calculation for a square cross-section of a rod.
Name of a file with the initial data: Square.cns
Formulation: Check the accuracy of the shear and torsional geometric properties calculation for a square cross-section of a rod.
References: Timoshenko S.P., Goodier J., Theory of Elasticity, M., Nauka, 1975.
Gruttmann F., Wagner W., Shear correction factors in Timoshenko’s beam theory for arbitrary shaped cross-sections // Comput. Mech. — 2001. — 27; No. 3 — 199–207.
Initial data:
| ν = 0.25 | - Poisson’s ratio; |
| a = 40 cm | - side length of a square. |
Design model: The design model is created by triangulation (the number of triangles ≈ 3000) on the basis of a model of the external contour. The external contour is a square. The number of vertices of the contour in a model is 4.
Results Obtained in Consul
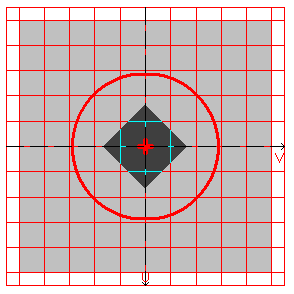
Design model, coordinate and principal axes, center of mass, ellipse of inertia, core of the section
Comparison of results:
|
Parameter |
Theory |
CONSUL |
Deviation, % |
|---|---|---|---|
|
Conventional shear area along the principal U-axis, Av,y cm2 |
1327,36 |
1332,135 |
0,359 |
|
Conventional shear area along the principal V-axis, Av,z cm2 |
1327,36 |
1332,135 |
0,359 |
|
Torsional moment of inertia, It cm4 |
360000 |
357205,548 |
0,77 |
|
Y-coordinate of the shear center, yb cm |
20 |
20 |
0 |
|
Z-coordinate of the shear center, zb cm |
20 |
20 |
0 |
Notes: Geometric properties can be determined analytically by the following formulas:
\[ I_{t} =\frac{a^{4}}{3}\left[ {1-\frac{192}{\pi ^{5}}\sum\limits_{n=1}^{\infty \infty } {\frac{1}{(2n-1)^{5}}\tanh \left( {\frac{\pi (2n-1)}{2}} \right)} } \right]\approx 2,25\left( {\frac{a}{2}} \right)^{4}; \] \[ y_{b} =a/2; \] \[ z_{b} =a/2; \]