Geometric Properties of Regular Polygons

 

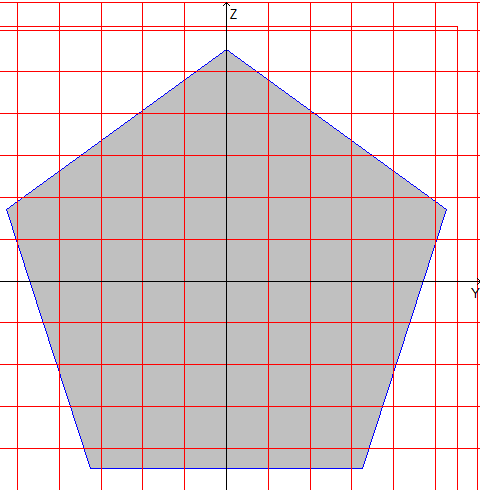
pentagon
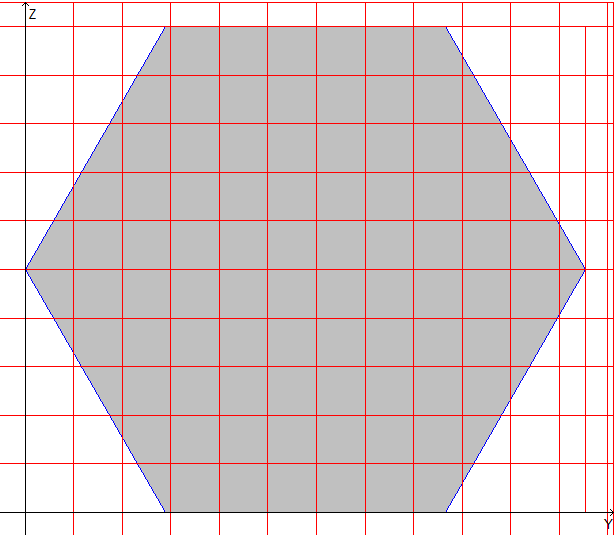
hexagon
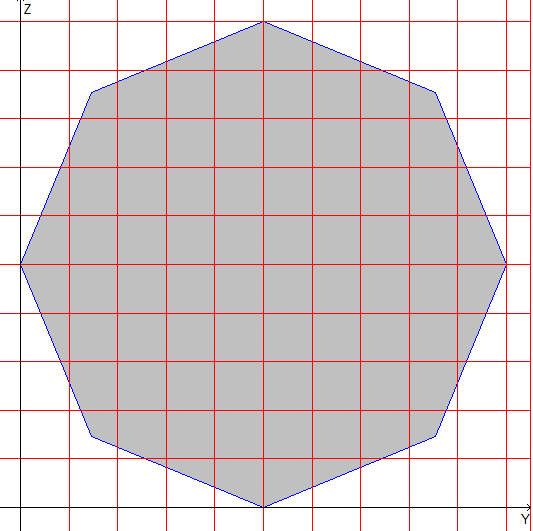
octagon

Aim: To check the accuracy of the torsional moment of inertia calculation for a rod cross-section in the form of a regular polygon.

Names of files with the initial data:

Pentagon.cns Hexagon.cns Octagon.cns

 

Formulation: Check the accuracy of the torsional geometric properties calculation for a rod cross-section in the form of a regular pentagon, hexagon and octagon.

References: Hassenpflug W.C., Torsion of uniform bars with polygon cross-section, Computers & Mathematics with Applications, 2003, 46, No. 2-3, 313–392.

Kovář A., Moment tuhosti v kroucení pravidelného pětiúhelníka, Aplikace matematiky, 1957, 2, No. 1, 58-65.

Initial data:

ν = 0.3	- Poisson’s ratio;
r = 10 cm	- radius of a circumscribed circle.

 

Design model: The design model is created by triangulation (the number of triangles ≈ 3000) on the basis of a model of the external contour. The external contour is a regular polygon. The number of vertices of the contour in a model is 5 (6, 8).

Results Obtained in Consul

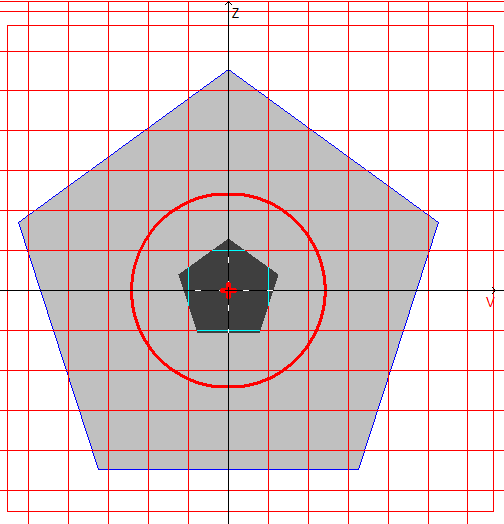
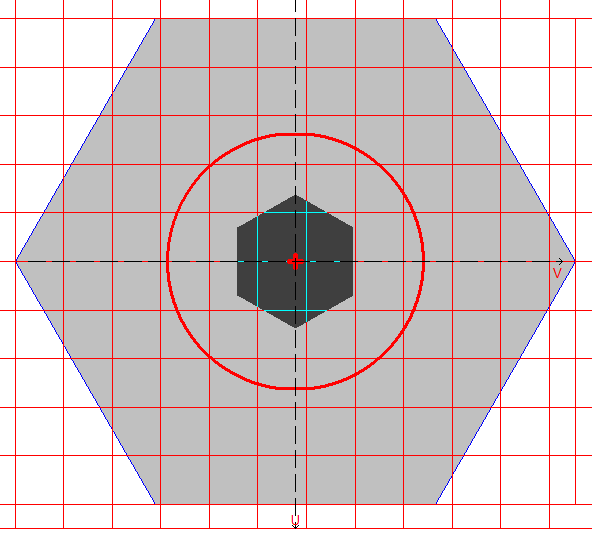
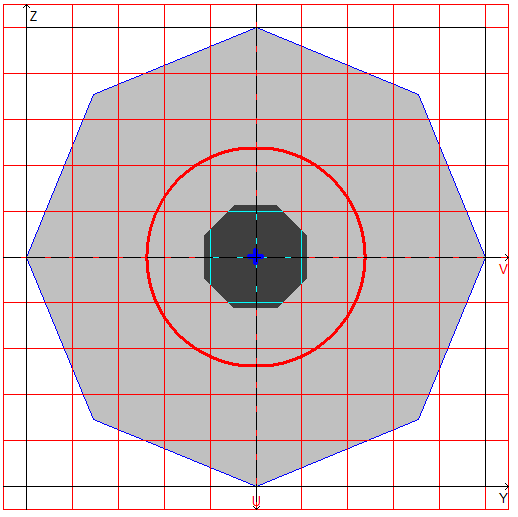
Design model, coordinate and principal axes, center of mass, ellipse of inertia, core of the section

Comparison of results:

	Parameter	Theory	CONSUL	Deviation, %
pentagon	Torsional moment of inertia, It cm4	8478,1	8312,915	1,98
hexagon		10384	10215,966	1,61
octagon		12556,6	12453,297	0,822

Notes: Geometric properties can be determined analytically by the following formulas:

\[ \text {пятиугольник }\quad  I_{t} \approx \mbox{0,84781}r^{4}; \]

\[ \text {шестиугольник}\quad  I_{t} \approx \mbox{1,03877}r^{4}; \]

\[ \text {воcьмиугольник}\quad I_{t} \approx \mbox{1,25566}r^{4}; \]