Geometric Properties of a Semicircle
Aim: To check the accuracy of the geometric properties calculation for a rod cross-section in the form of a semicircle.
Name of a file with the initial data: Disk2.cns
Formulation: Check the accuracy of the torsional geometric properties calculation for a rod cross-section in the form of a semicircle.
References: Young W.C., Budynas R.G., Roark's Formulas for Stress and Strain, New York , McGraw-Hill, New York, 2002.
Weisstein E.W., Torsional Rigidity, From MathWorld — A Wolfram Web Resource. http://mathworld.wolfram.com/TorsionalRigidity.html
Cowper G.R., The Shear Coefficient in Timoshenko's Beam, ASME Journal of Applied Mechanics, 1966, 33, 335-341.
Novojilov V.V., Theory of Elasticity, Moscow, State Union Publishing House of the Shipbuilding Industry, 1958, (§ VI.21).
Marinetti A., On the Accuracy of Shear Factors for Elastic Uniform Beams: Evaluation Using the Boundary Element Method, In "Materiali e Metodi Innovativi nell'Ingegneria Strutturale" Aracne Editrice, ISBN 978-88-548-2451-5, (2009).
Initial data:
| ν = 0.1 | - Poisson’s ratio; |
| d = 10 cm | - diameter of a circle. |
Design model: The design model is created by triangulation (the number of triangles ≈ 3000) on the basis of a model of the external contour. The external contour is a polygon approximating a semicircle. The number of vertices of the contour in a model is 33.
Results Obtained in Consul
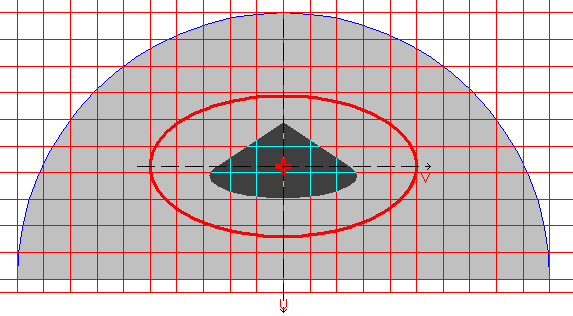
Design model, coordinate and principal axes, center of mass, ellipse of inertia, core of the section
Comparison of results:
|
Parameter |
Theory |
CONSUL |
Deviation, % |
|---|---|---|---|
|
Cross-sectional area, A cm2 |
39,269 |
39,207 |
0.16 |
|
Conventional shear area along the principal U-axis, Av,y cm2 |
30,239 |
29,071 |
3,862 |
|
Conventional shear area along the principal V-axis, Av,z cm2 |
34,691 |
33,29 |
4,03 |
|
Torsional moment of inertia, It cm4 |
182,25 |
183,05 |
0,438 |
|
Y-coordinate of the shear center, yb cm |
5 |
5 |
0 |
|
Z-coordinate of the shear center Z, zb cm |
2,55497 |
2,555 |
0,00117 |
Notes: Geometric properties can be determined analytically by the following formulas:
\[ A_{v,y} \approx A\frac{1+\nu }{1,305+1,273\nu }; \] \[ A_{v,z} \approx A\frac{(1+\nu )^{2}}{\frac{7}{6}+\left( {2+\frac{64}{45\pi ^{2}}} \right)\cdot \nu +\left[ {\frac{2}{3}+\frac{64}{15\pi ^{2}}-\sum\limits_{т=1}^\infty {\frac{1}{(2n-1)^{2}(2n+3)^{2}}} } \right]\cdot \nu^{2}}; \] \[ I_{t} =\left( {\frac{\pi }{2}-\frac{4}{\pi }} \right)\left( {\frac{d}{2}} \right)^{4}; \] \[ y_{b} =d/2; \] \[ z_{b} \approx \left( {\frac{4}{15\pi }\cdot \frac{3+3,05\nu }{1+\nu }} \right)d. \]
Differences in the position of the shear center are partially explained by the difference in the definition of the shear center (see Definitions of Geometric Properties).