Геометрические характеристики эллипса

Цель: Проверка точности вычислений геометрических характеристик сплошного эллиптического поперечного сечения стержня.

Формулировка задачи: Для сплошного эллиптического поперечного сечения стержня проверить точность вычисления геометрических характеристик.

Ссылки: С. П. Демидов, Теория упругости, Москва, Высшая школа, 1979.
А. И. Лурье, Теория упругости, Москва, Наука, 1970.

Исходные данные:

ν = 0.30	- коэффициент Пуассона;
a = 50 см	- размер большой полуоси эллиптического поперечного сечения (вдоль оси Y);
b = 30 см	- размер малой полуоси эллиптического поперечного сечения (вдоль оси Z).

 

Файл с исходными данными: Ellipse_Solid.cns

 

Расчетная модель: Расчетная модель образуется методом триангуляции (число треугольников ≈ 3000) на основе модели внешнего контура, импортируемого из графического редактора AutoCAD. Модель внешнего контура представляет собой многоугольник, вписанный в эллипс с заданными характеристиками и построенный в полярных координатах с шагом угла 3°. Количество вершин многоугольника в модели - 120.

 

Результаты решения в Консул

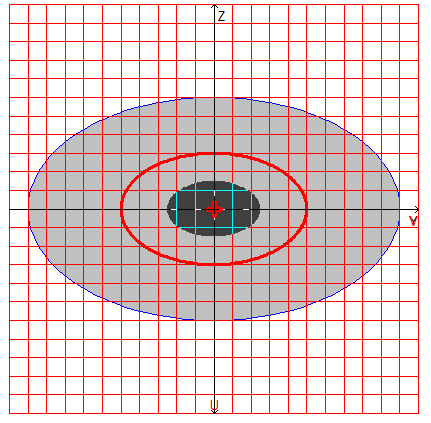
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения

 

Сравнение решений:

Параметр	Теория	КОНСУЛ	Отклонение, %
Площадь поперечного сечения, A см2	4712.389	4709.319	0.07
Условная площадь среза вдоль главной оси U, Av,y см2	3724.143	3702.975	0.57
Условная площадь среза вдоль главной оси V, Av,z см2	4147.170	4161.672	0.35
Угол наклона главных осей инерции, α рад	1.5708	1.5708	0.00
Момент инерции относительно центральной оси Y1, параллельной оси Y, Iy см4	1060287.521	1059491.143	0.08
Момент инерции относительно центральной оси Z1, параллельной оси Z, Iz см4	2945243.113	2939784.432	0.19
Момент инерции при свободном кручении, It см4	3118492.708	3064969.367	1.72
Секториальный момент инерции, Iw см6	97835065.337	95561910.155	2.32
Радиус инерции относительно оси Y1, iy см	15.000	14.980	0.13
Радиус инерции относительно оси Z1, iz см	25.000	24.991	0.04
Максимальный момент сопротивления относительно оси U, Wu+ см3	58904.862	58795.689	0.19
Минимальный момент сопротивления относительно оси U, Wu- см3	58904.862	58795.689	0.19
Максимальный момент сопротивления относительно оси V, Wv+ см3	35342.917	35316.371	0.08
Минимальный момент сопротивления относительно оси V, Wv- см3	35342.917	35316.371	0.08
Пластический момент сопротивления относительно оси U, Wpl,u см3	100000.000	99796.050	0.20
Пластический момент сопротивления относительно оси V, Wpl,v см3	60000.000	59820.326	0.30
Максимальный момент инерции, Iu см4	2945243.113	2939784.432	0.19
Минимальный момент инерции, Iv см4	1060287.521	1059491.143	0.08
Максимальный радиус инерции, iu см	25.000	24.985	0.06
Минимальный радиус инерции, iv см	15.000	14.999	0.01
Ядровое расстояние вдоль положительного направления оси Y (U), a u+ см	7.500	7.494	0.08
Ядровое расстояние вдоль отрицательного направления оси Y (U), a u- см	7.500	7.480	0.27
Ядровое расстояние вдоль положительного направления оси Z (V), a v+ см	12.500	12.491	0.07
Ядровое расстояние вдоль отрицательного направления оси Z (V), a v- см	12.500	12.491	0.07
Координата центра масс по оси Y, ym см	0.000	0.000	—
Координата центра масс по оси Z, zm см	0.000	0.000	—
Координата центра изгиба по оси Y, yb см	0.000	0.013	—
Координата центра изгиба по оси Z, zb см	0.000	0.040	—
Периметр, P см	255.180	255.180	0.00
Внутренний периметр, Pi см	0.000	0.000	—
Внешний периметр, Pe см	255.180	255.180	0.00
Полярный момент инерции, Ip см4	4005530.633	3993669.583	0.30
Полярный радиус инерции, ip см	29.155	29.136	0.07
Полярный момент сопротивления, Wp см3	80110.800	79872.926	0.30

 

Замечания: При аналитическом решении геометрические характеристики сплошного эллиптического поперечного сечения стержня определяются по следующим формулам:

\[ A=\pi \cdot a\cdot b; \] \[ A_{v,y} =\frac{3\cdot \left( {1+\nu } \right)^{2}\cdot \left( {a^{2}+3\cdot b^{2}} \right)^{2}\cdot b^{2}}{\left( {1+\nu } \right)^{2}\cdot \left( {22\cdot a^{2}+30\cdot b^{2}} \right)\cdot b^{4}+\left( {2\cdot \nu ^{2}\cdot a^{2}+\left( {4+8\cdot \nu +10\cdot \nu^{2}} \right)\cdot b^{2}} \right)\cdot a^{4}}\cdot \pi \cdot a\cdot b; \] \[ A_{v,z} =\frac{3\cdot \left( {1+\nu } \right)^{2}\cdot \left( {3\cdot a^{2}+b^{2}} \right)^{2}\cdot a^{2}}{\left( {1+\nu } \right)^{2}\cdot \left( {30\cdot a^{2}+22\cdot b^{2}} \right)\cdot a^{4}+\left( {\left( {4+8\cdot \nu +10\cdot \nu^{2}} \right)\cdot a^{2}+2\cdot \nu^{2}\cdot b^{2}} \right)\cdot b^{4}}\cdot \pi \cdot a\cdot b; \] \[ \alpha =0; \quad I_{y}=I_{v} =I_{1} =\frac{\pi \cdot a\cdot b^{3}}{4}; \quad I_{z} =I_{u} =I_{2} =\frac{\pi \cdot a^{3}\cdot b}{4}; \] \[ I_{t} =\frac{\pi \cdot a^{3}\cdot b^{3}}{a^{2}+b^{2}}; \quad I_{w} =\frac{\pi \cdot a^{3}\cdot b^{3}}{24}\cdot \left( {\frac{a^{2}-b^{2}}{a^{2}+b^{2}}} \right)^{2}; \] \[ i_{y} =i_{v} =\frac{b}{2}; \quad i_{z} =i_{u} =\frac{a}{2}; \] \[ W_{u+} =W_{u-} =\frac{\pi \cdot a^{2}\cdot b}{4}; \quad W_{v+} =W_{v-} =\frac{\pi \cdot a\cdot b^{2}}{4}; \] \[ W_{pl,u} =\frac{4\cdot a^{2}\cdot b}{3}; \quad W_{pl,v} =\frac{4\cdot a\cdot b^{2}}{3}; \] \[ a_{u+} =a_{u-} =\frac{b}{4}; \quad a_{v+} =a_{v-} =\frac{a}{4}; \] \[ y_{m} =y_{b} =z_{m} =z_{b} =0; \] \[P=P_{e} =4\cdot a\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right), \quad где: \quad E\left( x \right) \text {- полный эллиптический интеграл Лежандра второго рода;} \] \[ P\approx 4\cdot \left( {a+b} \right)-\frac{2\cdot \left( {4-\pi } \right)\cdot a\cdot b}{\sqrt[{\frac{3\cdot \pi -8}{8-2\cdot \pi }}]{\frac{a^{\frac{3\cdot \pi -8}{8-2\cdot \pi }}+b^{\frac{3\cdot \pi -8}{8-2\cdot \pi }}}{2}}}; \quad P\approx \pi \cdot \left( {a+b} \right); \quad P_{i} =0; \] \[ I_{12} =0; \quad I_{p} =\frac{\pi \cdot a\cdot b\cdot \left( {a^{2}+b^{2}} \right)}{4}; \quad i_{p} =\frac{\sqrt {a^{2}+b^{2}} }{2}; \quad W_{p} =\frac{\pi \cdot b\cdot \left( {a^{2}+b^{2}} \right)}{4}. \]