Геометрические характеристики квадрата

Цель: Проверка точности вычислений геометрических характеристик поперечного сечения стержня с формой в виде квадрата.

Формулировка задачи: Для поперечного сечения стержня с формой в виде квадрата проверить точность вычислений крутильных и сдвиговых геометрических характеристик.

Ссылки: С.П.Тимошенко, Дж.Гудьер, Теория упругости, М., Наука, 1975.
F.Gruttmann, W.Wagner, Shear correction factors in Timoshenko’s beam theory for arbitrary shaped cross-sections // Comput. Mech. — 2001. — 27; No. 3 — 199–207.

Исходные данные:

ν = 0.25	- коэффициент Пуассона;
a = 40 см	- размер стороны квадрата.

Файл с исходными данными: Square.cns

Расчетная модель: Расчетная модель образуется методом триангуляции (число треугольников ≈ 3000) на основе модели внешнего контура. Внеший контур представляет собой квадрат. Количество вершин контура в модели - 4.

Результаты решения в Консул

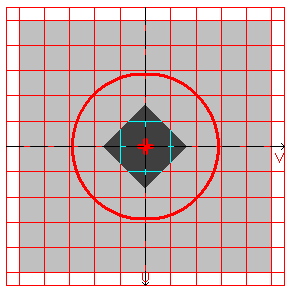
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения

Сравнение решений:

Параметр	Теория	КОНСУЛ	Отклонение, %
Условная площадь среза вдоль главной оси U, A_v,y см²	1327,36	1332,135	0,359
Условная площадь среза вдоль главной оси V, A_v,z см²	1327,36	1332,135	0,359
Момент инерции при свободном кручении, I_t см⁴	360000	357205,548	0,77
Координата центра изгиба по оси Y, y_b см	20	20	0
Координата центра изгиба по оси Z, z_b см	20	20	0

Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:

\[ I_{t} =\frac{a^{4}}{3}\left[ {1-\frac{192}{\pi ^{5}}\sum\limits_{n=1}^{\infty \infty } {\frac{1}{(2n-1)^{5}}\tanh \left( {\frac{\pi (2n-1)}{2}} \right)} } \right]\approx 2,25\left( {\frac{a}{2}} \right)^{4}; \] \[ y_{b} =a/2; \] \[ z_{b} =a/2; \]