Геометрические характеристики равностороннего треугольника

Цель: Проверка точности вычислений геометрических характеристик поперечного сечения стержня с формой в виде равностороннего треугольника.

Формулировка задачи: Для поперечного сечения стержня с формой в виде равностороннего треугольника проверить точность вычислений крутильных геометрических характеристик.

Ссылки: W.C.Young, R.G.Budynas, Roark's Formulas for Stress and Strain, New York , McGraw-Hill, New York, 2002.

Исходные данные:

ν = 0.3	- коэффициент Пуассона;
a = 40 см	- размер стороны равностороннего треугольника.

Файл с исходными данными: Triangle.cns

Расчетная модель: Расчетная модель образуется методом триангуляции (число треугольников ≈ 3000) на основе модели внешнего контура. Внеший контур представляет собой правильный треугольник. Количество вершин контура в модели – 3.

Результаты решения в Консул

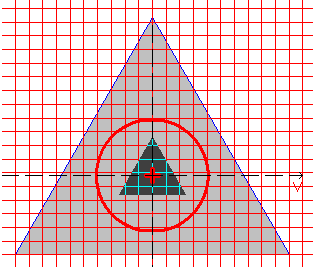
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения

Сравнение решений:

Параметр	Теория	КОНСУЛ	Отклонение, %
Момент инерции при свободном кручении, I_t см⁴	55425,625	54477,143	1.71
Координата центра изгиба по оси Y, y_b см	20	19,999	0,005
Координата центра изгиба по оси Z, z_b см	11,547	11,589	0,36

Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:

\[ I_{t} =\frac{\sqrt 3 }{80}a^{4}; \] \[ y_{b} =a/2; \] \[ z_{b} =\frac{a}{2\sqrt 3 }. \]