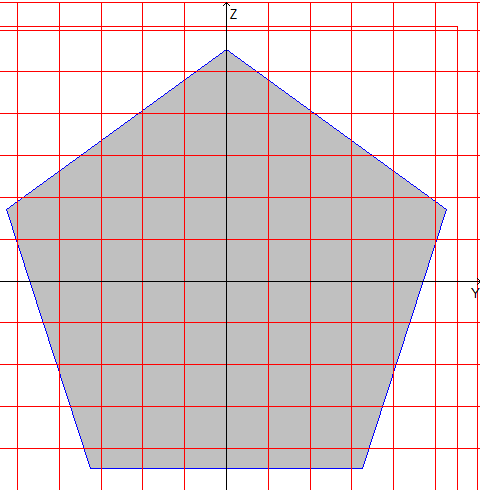
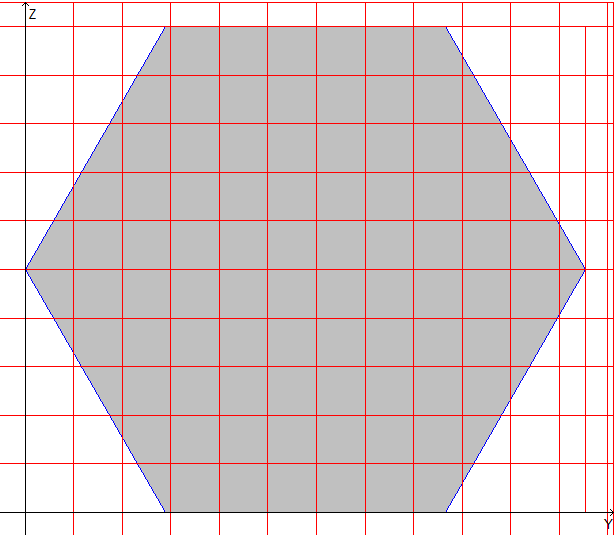
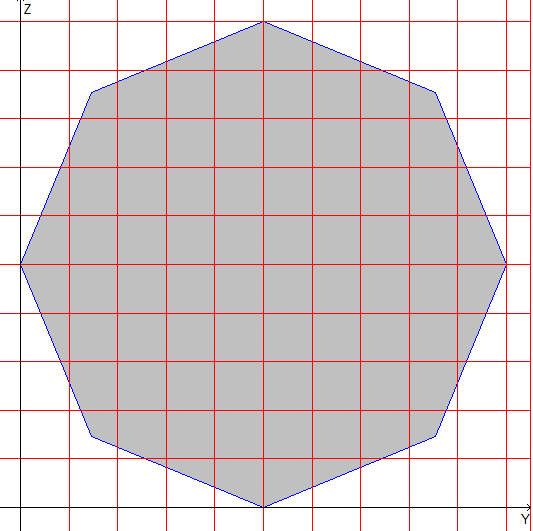
Геометрические характеристики правильных многоугольников
|
пятиугольник |
|
|
|
шестиугольник |
|
|
|
восьмиугольник |
|
|
Цель: Проверка точности вычислений момента инерции на кручение поперечного сечения стержня с формой правильного многоугольника.
Формулировка задачи: Для поперечного сечения стержня с формой в виде правильного пятиугольника, шестиугольника и восьмиугольника проверить точность вычислений крутильных геометрических характеристик.
Ссылки: W.C. Hassenpflug, Torsion of uniform bars with polygon cross-section, Computers & Mathematics with Applications, 2003, 46, No. 2-3, 313–392.
A.Kovár, Moment tuhosti v kroucení pravidelného petiúhelníka, Aplikace matematiky, 1957, 2, No. 1, 58-65.
Исходные данные:
| ν = 0.3 | - коэффициент Пуассона; |
| r = 10 см | - радиус описанной окружности. |
| Файлы с исходными данными: | Pentagon.cns Hexagon.cns Octagon.cns |
Расчетная модель: Расчетная модель образуется методом триангуляции (число треугольников ≈ 3000) на основе модели внешнего контура. Внеший контур представляет собой правильный многоугольник. Количество вершин контура в модели – 5 (6, 8).
Результаты решения в Консул
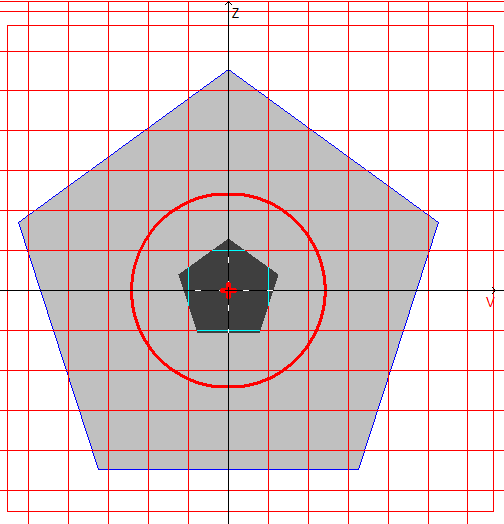
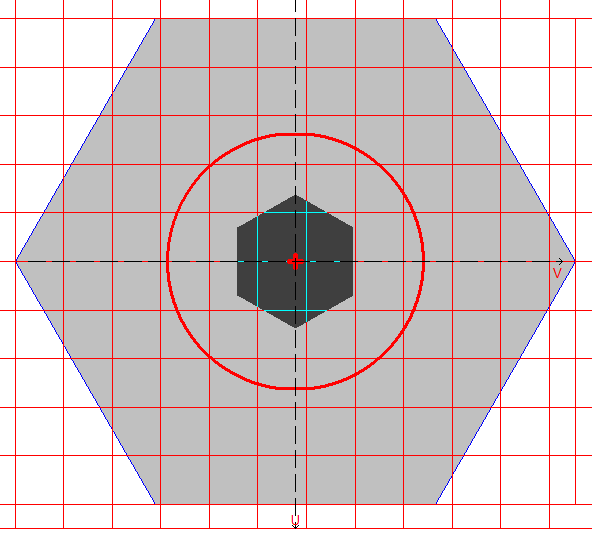
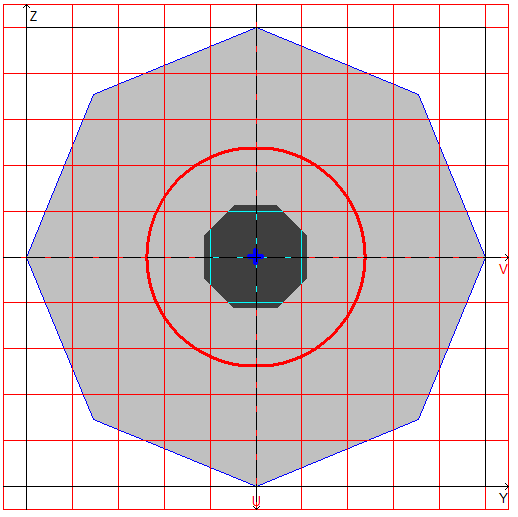
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения
Сравнение решений:
|
|
Параметр |
Теория |
КОНСУЛ |
Отклонение, % |
|---|---|---|---|---|
|
пятиугольник |
|
8478,1 |
8312,915 |
1,98 |
|
шестиугольник |
10384 |
10215,966 |
1,61 |
|
|
воьмиугольник |
12556,6 |
12453,297 |
0,822 |
Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:
\[ \text {пятиугольник }\quad I_{t} \approx \mbox{0,84781}r^{4}; \]
\[ \text {шестиугольник}\quad I_{t} \approx \mbox{1,03877}r^{4}; \]
\[ \text {воcьмиугольник}\quad I_{t} \approx \mbox{1,25566}r^{4}; \]