Геометрические характеристики полукруга
Цель: Проверка точности вычислений геометрических характеристик поперечного сечения стержня с формой полукруга.
Формулировка задачи: Для поперечного сечения стержня с формой в виде полукруга проверить точность вычислений крутильных геометрических характеристик.
Ссылки: W.C.Young, R.G.Budynas, Roark's Formulas for Stress and Strain, New York , McGraw-Hill, New York, 2002.
E.W.Weisstein, "Torsional Rigidity." From MathWorld — A Wolfram Web Resource. http://mathworld.wolfram.com/TorsionalRigidity.html
G.R.Cowper, The Shear Coefficient in Timoshenko's Beam, ASME Journal of Applied Mechanics, 1966, 33, 335-341.
В. В.Новожилов, Теория упругости, Москва, Государственное союзное издательство судостроительной промышленности, 1958, (§ VI.21).
Marinetti A., On the Accuracy of Shear Factors for Elastic Uniform Beams: Evaluation Using the Boundary Element Method, In "Materiali e Metodi Innovativi nell'Ingegneria Strutturale" Aracne Editrice, ISBN 978-88-548-2451-5, (2009).
Исходные данные:
| ν = 0.1 | - коэффициент Пуассона; |
| d = 10 см | - диаметр круга. |
Файл с исходными данными: Disk2.cns
Расчетная модель: Расчетная модель образуется методом триангуляции (число треугольников ≈ 3000) на основе модели внешнего контура. Внеший контур представляет собой многоугольник аппроксимирующий полукруг. Количество вершин контура в модели – 33.
Результаты решения в Консул
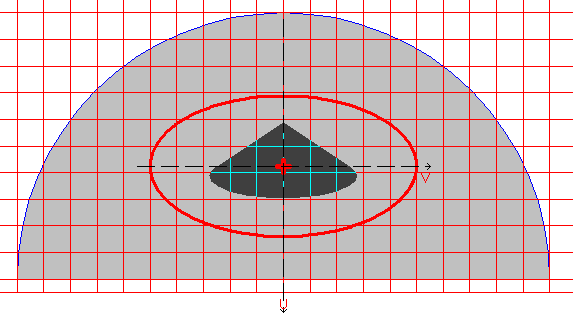
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения
Сравнение решений:
|
Параметр |
Теория |
КОНСУЛ |
Отклонение, % |
|---|---|---|---|
|
Площадь поперечного сечения, A см2 |
39,269 |
39,207 |
0.16 |
|
Условная площадь среза вдоль главной оси U, Av,y см2 |
30,239 |
29,071 |
3,862 |
|
Условная площадь среза вдоль главной оси V, Av,z см2 |
34,691 |
33,29 |
4,03 |
|
Момент инерции при свободном кручении, It см4 |
182,25 |
183,05 |
0,438 |
|
Координата центра изгиба по оси Y, yb см |
5 |
5 |
0 |
|
Координата центра изгиба по оси Z, zb см |
2,55497 |
2,555 |
0,00117 |
Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:
\[ A_{v,y} \approx A\frac{1+\nu }{1,305+1,273\nu }; \] \[ A_{v,z} \approx A\frac{(1+\nu )^{2}}{\frac{7}{6}+\left( {2+\frac{64}{45\pi ^{2}}} \right)\cdot \nu +\left[ {\frac{2}{3}+\frac{64}{15\pi ^{2}}-\sum\limits_{т=1}^\infty {\frac{1}{(2n-1)^{2}(2n+3)^{2}}} } \right]\cdot \nu^{2}}; \] \[ I_{t} =\left( {\frac{\pi }{2}-\frac{4}{\pi }} \right)\left( {\frac{d}{2}} \right)^{4}; \] \[ y_{b} =d/2; \] \[ z_{b} \approx \left( {\frac{4}{15\pi }\cdot \frac{3+3,05\nu }{1+\nu }} \right)d. \]