Геометрические характеристики квадрата с центральным квадратным отверстием

Цель: Проверка точности вычислений момента инерции на кручение поперечного сечения стержня с отверстием.

Формулировка задачи: Для поперечного сечения стержня с формой в виде квадрата с центральным квадратным отверстием проверить точность вычислений крутильных геометрических характеристик.

Ссылки: Н.Х.Арутюнян Б.Л.Абрамян, Кручение упругих тел, Физматгиз, Москва, 1963 (см. § III.1.7).

Исходные данные:

ν = 0.3	- коэффициент Пуассона;
b = 100 см	- геометрические размеры.
d = 40 см

 

Файл с исходными данными: SquareWithHole.cns

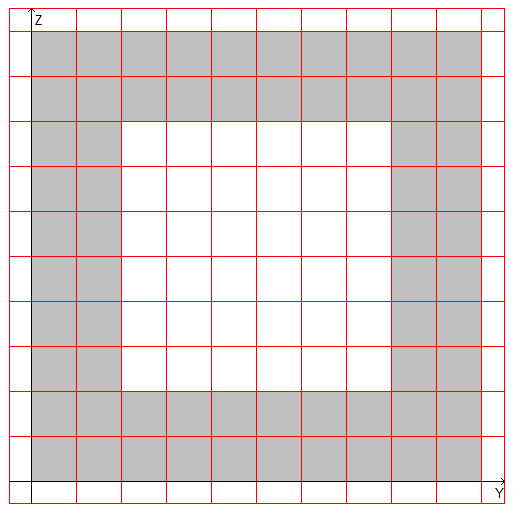
Расчетная модель: Расчетная модель образуется методом триангуляции (число треугольников ≈ 3000) на основе модели внешнего и внутреннего контуров. Внеший контур представляет собой квадрат, внутренний — центрально расположенный квадрат. Количество вершин контура в модели – 8.

Результаты решения в Консул

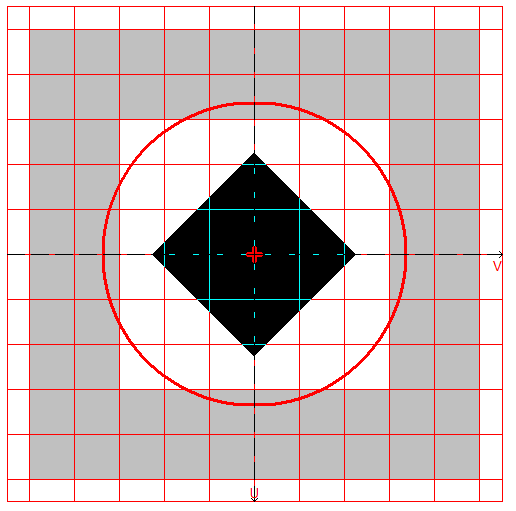
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения

Сравнение решений:

Параметр	Теория	КОНСУЛ	Отклонение, %
Момент инерции при свободном кручении, It см4	189095936	188022747,341	0,56

Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:

\[ I_{t} \approx 8\left[ {\left( {\frac{b}{d}} \right)^{3}-1,2704\left( {\frac{b}{d}} \right)^{2}+0,661\left( {\frac{b}{d}} \right)-0,1043} \right]d^{4}. \]