Decor

Check of the Load-bearing Capacity of a Bottom Truss Chord Section under Central Tensio

Objective: Check of the calculation of the resistance of sections.

Task: Verify the correctness of the strength analysis of normal sections.

References: Nasonov S.B. Manual on design and analysis of building structures. – M: ASV Publishing House, 2013. – p. 62-63.

Initial data file:
Example 3.SAV;
report – Decor 3.doc.

Software version: DECOR 21.1.1.1, 17.02.2016.

Compliance with the codes: SNiP ІІ-25-80, SP 64.13330.2011.

Initial data from the source:

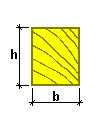
b×h = 15×10 см Section sizes of the element
l = 3 м Member length
d = 1,6 см Diameter of the hole
N = 60 кН Tensile force

Material of the element: pine.
Grade of wood: 2.
Operating conditions class: 1 (А2 according to SNiP ІІ-25-80).

 

DECOR initial data:

 

Importance factor γn = 1

Service factors

Service factor  for temperature and humidity operating conditions mВ

1

Allowance for the temperature conditions of operation mТ

1

Allowance for the duration of loading md

1

Service factor under short-term loads mn

1

Factor that allows for the effect of impregnation with protective substances mа

1

Wood species - Pine
Grade of wood - 2
Limit slenderness of members in tension - 200
Limit slenderness of members in compression - 120
Member length 3m

Effective length factor in the XoY plane - 1

Effective length factor in the XoZ plane - 1

 

Section:

b = 150 mm
h = 100 mm

Non-glued timber section

 

Weakening not reaching the edge
Area of the weakening - 24 cm2

Forces:

N = 60 kN
My = 0 kN*m
Qz = 0 kN
Mz = 0 kN*m
Qy = 0 kN

Comparison of solutions:

File

Example 3.SAV

Report file

Decor 3.doc

Check

Strength of the member under a longitudinal tensile force

Theory

0,47/0,56 = 0,839

DECOR

0,85

Deviation, %

1,3 %

Comments:

  1. The area of the weakening in the section is determined as the product of the width of the cross-section by the diameter of the hole 15×1,6 = 24 cm2.
  2. Service factor for 1 (А2) class mв = 1 (table 5 of SNiP ІІ-25-80, table 7 of SP 64.13330.2011).
  3. Limit slenderness of the truss chord in tension (not in the vertical plane) is equal to λmax = 200 (table 14 of SNiP ІІ-25-80, table 17 of SP 64.13330.2011).
  4. Boundary conditions of the element have to be specified in DECOR. Since they are not determined in the problem, it is assumed that the element is simply supported (μy = μz = 1).