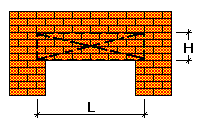
Calculation of the Coursed Masonry Lintel
Objective: Check of the calculation of masonry lintels.
Task: Verify the correctness of the calculation of lintels.
Compliance with the codes: SNiP II-22-81, SP 15.13330.2012.
Initial data file:
Example 5.1.SAV;
ComeIn.doc — report
Initial data:
The intermediate lintel has a span of 1,78 m, and is made of molded clay brick of grade 100 with regular cement mortar of grade 25. The elastic characteristic of masonry is α = 1000. The thickness of the wall is 510 mm, the specific weight of masonry is 1,8 t/m3. The lintel is constructed in summer. The distance from the bottom of the lintel to the supported panels is 60 cm. The design load on the floor panels taking into account their self-weight is 14,5 kN/m2. The distance between the load-bearing walls is 4,8 m.
Analytical solution:
Determine the effective height of the lintel
\[ c=\frac{1}{3}l=\frac{1}{3}178=60 см \]
Design section of the lintel – width 51 cm, height 60 cm.
Since the smaller size of the design section is greater than 30 cm, the factor for sustained load is taken as mg = 1,0.
Then the design load from the self-weight of the lintel and the masonry above it is
\[ q_{1} = bhg\gamma_{f} =\quad 0,51×0,6×18×1,1 = 6000 кH/м \]
Since the floor panels are supported on the masonry below the height equal to the span, the load from them is transferred to the lintel. The design load per 1 r.m. will be
\[ q_{2} = 14,5×4,8×0,5 = 34,8 кН/м \]
Bending moment in the crown of the lintel
\[ M=\frac{(q_{1} +q_{2} )l^{2}}{8}=\frac{(6+34,8)1,78^{2}}{8}=16,15 кHм \]
Distance from the top of the design part of the lintel to the pressure center in the crown and from the bottom of the lintel to the pressure center in the imposts
\[ r=0,15c=0,15×60 = 9 см. \]
Then the design thrust is
\[ H=\frac{M}{c-2r}=\frac{16,15}{60-2\cdot 9}=38,5 кH, \]
and the eccentricity of its application is
\[ e_{0} =\frac{c}{2}-r=\frac{60}{2}-9=21 см. \]
The height of the compressed area
\[ h_{c} =h-2e_{0} =60-2×21 = 18 см. \]
The check of stability under eccentric compression in the wall plane is the main one. The lintel is assumed to be partially clamped in the piers, and the effective length factor is taken as 0,67. The stability of the lintel out of the wall plane is assumed to be provided.
The effective length of the lintel
\[ l_{0} =0,67l=0,67×178 = 119,3 м \]
At the ratios \( \lambda_{h} =\frac{l_{0} }{\min (h,b)}=\frac{119,3}{51}=2,34 \), then the buckling coefficient is \( \phi=1 \)
and
\( \lambda_{hc} =\frac{l_{0} }{h_{c} }=\frac{119,3}{18}=9,889, \), then the buckling coefficient is \( \phi_{c} =0,882 \)
\[ \phi_{1} =\frac{\phi +\phi_{c} }{2}=\frac{1+0,882}{2}=0,941 \]
Coefficient allowing for the batten effect
\[ \omega =1+\frac{e_{0} }{h}=1+\frac{21}{60}=1,35<1,45. \]
Value of the compressed area of the section
\[ A_{c} =A(1-\frac{2e_{o} }{h})=51\times 60(1-2\frac{21}{60})=917 см^{2} \]
Then the load-bearing capacity of the lintel is
\( N_{adm} =m_{g} \phi_{1} RA_{c} \omega =1×0,941×1,3х91700×1,35 = 151,4 кH \quad H = 38.5 кH, \), i.e. the load-bearing capacity of the lintel is provided.
KAMIN initial data
Importance factor γn = 1
Importance factor (serviceability limit state) = 1
Age of masonry - up to a year
Construction season - summer
Working life is 25 years
Stone/brick - Molded clay brick
Stone/brick grade - 100
Mortar - regular cement with mineral plasticizers
Mortar grade - 25
Specific weight of masonry 1,8 T/m3
Structure:
|
|
H = 0,6 m |
Loads
Factor for sustained load 1
Load application height 0,6 m 
Comparison of solutions:
|
Check |
Stability of a lintel |
|
Manual |
38,5/151,4 = 0,254 |
|
KAMIN |
0,247 |
|
Deviation, % |
2,8 % |