Strength and Stiffness Analysis of Stringers for a Complex Stub Girder System
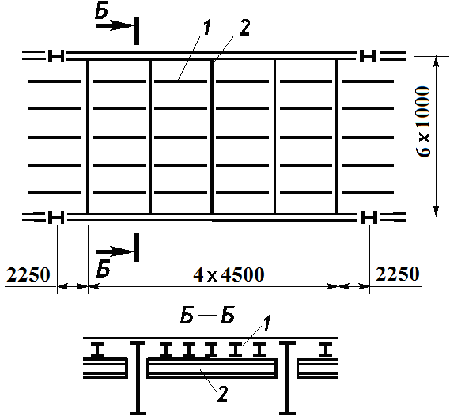
1 – stringer
2 – secondary beam
Objective: Check the mode for calculating and selecting beams
Task: Select a rolled I-beam for the stringers with a span of 4,5 m in a complex stub girder system. The top chord of the stringers is continuously restrained by the floor plate.
References: Steel Structures: Student Handbook / [Kudishin U.I., Belenya E.I., Ignatieva V.S and others] - 13-th ed. rev. - M.: Publishing Center "Academy", 2011. p. 183.
Compliance with the codes: SNiP II-23-81*, SP 16.13330, DBN B.2.6-163:2010.
Initial data file:
3.2.sav;
report — Kristall3.2.doc
Initial data:
| а = 1,0 m | Spacing of stringers; |
| qн = (0,77 + 20) кН/м2 ×1 m = 20,77 kN/m | Total characteristic load; |
| q1 = 1,05×0,77 kN/m2 ×1 m = 0,8085 kN/m | Design permanent load; |
| q2 = 1,2×20 kN/m2 ×1 m = 24 kN/m | Design temporary load; |
| Ry = 23 kN/cm2, | Steel grade C235; |
| l = 4,5 m | Beam span; |
| [ f ] = 1/250×4,5 м = 18 mm | Limit deflection; |
| γc = 1 | Service factor; |
| Wx = 288,33 cm3 | Selected I-beam No.24 GOST 8239-89; |
| Ix = 3460 cm4. |
KRISTALL parameters:
Steel: C235
Group of structures according to the table 50* of SNiP II-23-81* 4
Importance factor γn = 1
Importance factor (serviceability limit state) = 1
Service factor 1

Structure:
Restraints against lateral displacements and rotations:
|
|
Left |
Right |
|---|---|---|
|
Displacement along Y |
Restrained |
Restrained |
|
Displacement along Z |
Restrained |
Restrained |
|
Rotation about Y |
|
|
|
Rotation about Z |
|
|
Continuous restraint of the compressed chord out of the bending plane
Section:
Profile: I-beam with sloped inner flange surfaces GOST 8239-89 24
Manual calculation:
1. Design bending moment acting in the beam span:
\[ M_{\max } =\frac{q_{\Sigma } l^{2}}{8}=\frac{\left( {0,8085+24} \right)\cdot 4,5^{2}}{8}=62,7965 \quad kNm. \]
2. Necessary beam section modulus assuming that the deformations of steel are elastic:
\[ W=\frac{M_{\max } }{R_{y} }=\frac{62,7965\cdot 100}{23}=273,028 \quad cm^{3}. \]
3. Maximum deflection occurring in the middle of the beam span:
\[ f_{\max } =\frac{5}{384}\cdot \frac{q_{н} l^{4}}{EI_{x} }=\frac{5}{384}\cdot \frac{20,77\cdot 4,5^{4}}{2,06\cdot 10^{5}\cdot 10^{3}\cdot 3460\cdot 10^{-8}}=15,56 \quad mm. \]
Comparison of solutions:
|
Factor |
Strength under action of lateral force |
Strength under action of bending moment |
Stability of in-plane bending under moment |
Maximum deflection |
|---|---|---|---|---|
|
Manual calculation |
– |
273,028/288,33 = 0,947 |
– |
15,56/18 = 0,864 |
|
KRISTALL |
0,352 |
0,947 |
0,947 |
15,56/18 = 0,864 |
|
Deviation from the manual calculation, % |
0,0 |
0,0 |
0,0 |
0,0 |
|
Source |
– |
0,858 |
– |
0,87 |
Comments:
- The check of tangential stresses was not performed in the manual calculation due to the absence of weakenings and a relatively large thickness of the beam webs.
- The check of the general stability of the beam was not performed in the manual calculation, because the compressed beam chord is restrained against lateral displacements out of the bending plane by a welded floor plate.
- In the source the check of the beam strength under the action of the bending moment was performed taking into account the development of the limited plastic deformations.
- The check of the beam strength taking into account the development of the limited plastic deformations was not performed, because according to the codes this calculation is possible only when the beam web has stiffeners. In the initial data of the example the stringer was specified without any intermediate stiffeners.

