Analysis of a Lattice Axially Compressed Column from Two Rolled Channels

Objective: Check the mode for calculating columns of lattice cross-section

Task: Check the design lattice section from two channels on battens for the axially compressed column with a height of 6,5 m.

Source: Steel Structures: Student Handbook / [Kudishin U.I., Belenya E.I., Ignatieva V.S and others] - 13-th ed. rev. - M.: Publishing Center "Academy", 2011. p. 257.

Compliance with the codes: SNiP II-23-81*, SP 16.13330, DBN B.2.6-163:2010.

Initial data file:

5.2.sav;
report — Kristall-5.2.doc

Initial data:

l = 6 m	Column height;
μ = 1	Pinned restraint;
N = 1400 kN	Design compressive force;
γ_c = 1	Service factor;
R_y = 24 kN/cm²	Steel grade C245;
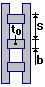
В = 300 mm	Distance between the outer faces of the chord;
b = 170 mm, s = 1120 mm	Batten height, distance between the batten axes;
t = 10 mm	Batten thickness;
A = 70,4 cm², I_y = 8320 cm⁴, I_z = 11576,86 cm⁴ i_y = 10,871 cm, i_z = 12,824 cm	Geometric properties of the lattice section;
A_b = 35,2 cm², I_b = I_z = 262 cm⁴ i_y = 10,871 cm, i_z = 2,728 cm W_b,z,min = 37,269 cm³	Geometric properties of the chord section;

KRISTALL parameters:

Steel: C245
Group of structures according to the table 50* of SNiP II-23-81* 3
Importance factor 1
Service factor 1
Member length – 6 m
Limit slenderness for members in compression: 180 - 60α
Limit slenderness for members in tension: 250

Section:

Profile: Channel with sloped inner flange surfaces GOST 8240-89 27

Lattice

b = 170 mm
t₀ = 10 mm
s = 1120 mm

Manual calculation (SNiP II-23-81*):

1. Moment of inertia and section modulus of one batten with respect to its own axis:

\[ I_{s} =\frac{t_{0} b^{3}}{12}=\frac{1\cdot 17^{3}}{12}=409,4167 \quad см^{4}; \] \[ W_{s} =\frac{t_{0} b^{2}}{6}=\frac{1\cdot 17^{2}}{6}=48,167 \quadсм^{3}. \]

2. Distance between chord axes:

\[ b=B-2z_{0} =30-2\cdot 2,47=25,06 \quad см. \]

3. Slenderness of one of the chords in the sections between the battens (in the clear):

\[ \lambda_{1,y} =\frac{l_{1,y} }{i_{1,y} }=\frac{600}{10,871}=55,193; \quad \bar{{\lambda }}_{1,y} =\lambda_{1,y} \sqrt {\frac{R_{y} }{E}} =55,193\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,884\le 5; \] \[ \lambda_{1,z} =\frac{l_{1,z} }{i_{1,z} }=\frac{s-b}{i_{1,z} }=\frac{112-17}{2,728}=34,824<40; \quad \bar{{\lambda }}_{1,z} =\lambda_{1,z} \sqrt {\frac{R_{y} }{E}} =34,824\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,1886\le 5. \]

4. Column slenderness and respective conditional slenderness:

\[ \lambda_{y} =\frac{l_{ef,y} }{i_{y} }=\frac{600}{10,871}=55,193; \quad \Rightarrow \quad \bar{{\lambda }}_{y} =\lambda_{y} \sqrt {\frac{R_{y} }{E}} =55,193\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,884<2,5; \] \[ \lambda_{z} =\frac{l_{ef,z} }{i_{z} }=\frac{600}{12,824}=46,787. \]

5. Reduced and conditional reduced slenderness of the column with respect to the free axis:

При \( \frac{I_{s} s}{I_{b} b}=\frac{409,4167\cdot 112}{262\cdot 25,06}=6,984>5: \)

\[ \lambda_{z} =\lambda_{ef,z} =\sqrt {\lambda_{z}^{2} +\lambda_{1,z}^{2} } =\sqrt {46,787^{2}+34,824^{2}} =58,3244; \] \[ \bar{{\lambda }}_{z} =\lambda_{z} \sqrt {\frac{R_{y} }{E}} =58,3244\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,991<2,5. \]

6. Buckling coefficients:

\[ \varphi_{y} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{y} \sqrt {\bar{{\lambda }}_{y} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)\cdot 1,884\sqrt {1,884} =0,8279; \] \[ \varphi_{z} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{z} \sqrt {\bar{{\lambda }}_{z} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)\cdot 1,991\sqrt {1,991} =0,813. \]

7. Limit compressive forces causing the column buckling about the respective axes:

\[ N_{b,y} =\varphi_{y} AR_{y} \gamma_{c} =0,8279\cdot 70,4\cdot 24\cdot 1=1398,8 \quad кН; \] \[ N_{b,z} =\varphi_{z} AR_{y} \gamma_{c} =0,813\cdot 70,4\cdot 24\cdot 1=1373,645 \quad кН. \]

8. Conditional shear force Q_fic:

\[ Q_{fic} =7,15\cdot 10^{-6}\left( {2330-\frac{E}{R_{y} }} \right)\frac{N}{\varphi_{z} }=7,15\cdot 10^{-6}\left( {2330-\frac{2,06\cdot 10^{5}}{240}} \right)\frac{1400}{0,813}=18,1198 \quad кН. \]

9. Force F, shearing the batten, and moment M₁, bending the batten in its plane:

\[ F=\frac{Q_{s} s}{b}=\frac{Q_{fic} s}{2b}=\frac{18,1198\cdot 112}{2\cdot 25,06}=40,4912 \quad кН; \] \[ M_{1} =\frac{Q_{s} s}{2}=\frac{Q_{fic} s}{4}=\frac{18,1198\cdot 112}{4}=507,3544 \quad кНсм. \]

10. Load-bearing capacity of the batten under bending:

\[ W_{s} R_{y} \gamma_{c} =48,167\cdot 24\cdot 1=1156,01 \quad кНсм. \]

11. Bending moment acting on the column chord and caused by the bending of the batten:

\[ M_{b} =2M_{1} =2\cdot 507,3544=1014,7088 \quad кНсм. \]

12. Load-bearing capacity of the chord under bending in the batten plane:

\[ W_{b,z,\min } R_{y} \gamma_{c} =37,269\cdot 24\cdot 1=894,456 \quad кНсм. \]

13. Strength of the chord under the combined action of the longitudinal force and bending moment in the batten plane without taking the plasticity into account:

\[ \frac{1}{R_{y} \gamma_{c} }\left( {\frac{N}{A}+\frac{M_{b} }{W_{b,z,\min } }} \right)=\frac{1}{24\cdot 1}\left( {\frac{1400}{70,4}+\frac{1014,7088}{37,269}} \right)=1,963. \]

14. Buckling coefficients for a chord:

\[ \varphi_{y} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{1,y} \sqrt {\bar{{\lambda }}_{1,y} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)1,884\sqrt {1,884} =0,828; \] \[ \varphi_{z} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\lambda_{1,z} \sqrt {\lambda_{1,z} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)\cdot 1,1886\sqrt {1,1886} =0,914. \]

15. Load-bearing capacity of the chord under compression:

\[ \varphi_{y} AR_{y} \gamma_{c} =0,828\cdot 35,2\cdot 24\cdot 1=699,398 \quad кН; \] \[ \varphi_{z} AR_{y} \gamma_{c} =0,914\cdot 35,2\cdot 24\cdot 1=772,1472 \quad кН. \]

16. Relative eccentricity, cross-section shape coefficient, reduced eccentricity, and buckling coefficient under eccentric compression of the chord

\[ m_{z} =\frac{M_{z} }{N}\cdot \frac{A_{b} }{W_{b,z,\min } }=\frac{1014,7088}{700}\cdot \frac{35,2}{37,269}=1,36911\le 5; \] \[ \frac{A_{f} }{A_{w} }=\frac{16,2}{19,95}=0,812; \] \[ \eta =\left( {1,25-0,05m_{z} } \right)-0,01\left( {5-m_{z} } \right)\bar{{\lambda }}_{1,z} =\left( {1,25-0,05\cdot 1,36911} \right)-0,01\left( {5-1,36911} \right)\cdot 1,1886=1,13838 \]

(for the section type 9 according to the table 73 of SNiP ІІ-23-81* when \(\frac{A_{f} }{A_{w} }=0,5);\)

\[ \eta =\left( {1,5-0,1m_{z} } \right)-0,02\left( {5-m_{z} } \right)\bar{{\lambda }}_{1,z} =\left( {1,5-0,1\cdot 1,36911} \right)-0,02\left( {5-1,36911} \right)\cdot 1,1886=1,27678 \]

(for the section type 9 according to the table 73 of SNiP ІІ-23-81* when \( \frac{A_{f} }{A_{w} }=1,0); \)

\(\eta =1,2247\) (for the section type 9 according to the table 73 of SNiP ІІ-23-81* when \( \frac{A_{f}}{A_{w} }=0,812);\)

\( \eta =1,45+0,04m_{z} =1,45+0,04\cdot 1,36911=1,50476 \) (for the section type 11 according to the table 73 of SNiP ІІ-23-81* when \( \frac{A_{f} }{A_{w} }=0,5);\)

\( \eta =1,8+0,12m_{z} =1,8+0,12\cdot 1,36911=1,9643\) (for the section type 11 according to the table 73 of SNiP ІІ-23-81* when \(\frac{A_{f} }{A_{w} }=1,0)\);

\(\eta =1,7915\) (for the section type 11 according to the table 73 of SNiP ІІ-23-81* when \(\frac{A_{f} }{A_{w} }=1,33811);\)

\[ m_{z,ef} =\eta m_{z} =1,7915\cdot 1,36911=2,453; \] \(\varphi_{e} =0,4174\) (according to the table 74 of SNiP ІІ-23-81*).

17. Stability check of the chord in the batten bending plane:

\[ \frac{N}{2\varphi_{e} A_{b} }=\frac{1400}{2\cdot 0,4174\cdot 35,2}=47,6434 \quad кН/см^{2} \quad >R_{y} \gamma_{c} =24\cdot 1=24 \quad кН/см^{2}. \]

18. Stability check of the chord out of the batten bending plane is performed as a stability check of an axially compressed bar in the respective plane according to Sec. 5.32 of SNiP II-23-81*.

Comparison of solutions:

Factor	Source	Manual calculation	KRISTALL
General stability of a bar under axial compression in XoY plane	24/24=1	1400/1373,645 = 1,019	1,019
General stability of a bar under axial compression in XoZ plane	23,6/24=0,983	1400/1398,82 = 1,001	1,001
Resistance of a batten to bending	–	507,3544/1156,01 = 0,439	0,439
Strength under action of bending moment M_z	–	1014,7088/894,456 = 1,134	1,134
Strength under combined action of longitudinal force and bending moments, no plasticity	–	1,963	1,963
Stability of chord under compression in XoY plane	–	700/772,1472 = 0,9066	0,907
Stability of chord under compression in XoZ plane	23,6/24=0,983	700/699,398 = 1,001	1,001
Stability of chord in the moment M_z plane under eccentric compression	–	47,6434/24 = 1,985	1,985
Stability of chord out of the moment M_z plane under eccentric compression	–	24,01735/24 = 1,001	1,001
Limit slenderness in XoY plane	–	58,3244/120 = 0,486	0,486
Limit slenderness in XoZ plane	–	55,193/120 = 0,46	0,46