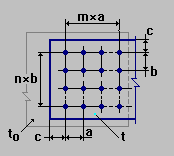
Analysis of an Erection Joint in the Beam Chord with High Strength Bolts

Objective: Check the mode for calculating friction bolted connections

Task: Check the erection joint of the chords of a compound I-beam with high strength bolts.

Source: Steel Structures: Student Handbook / [Kudishin U.I., Belenya E.I., Ignatieva V.S and others] - 13-th ed. rev. - M.: Publishing Center "Academy", 2011. p. 216.

Compliance with the codes: SNiP II-23-81*, SP 16.13330, DBN B.2.6-163:2010.

Initial data file:

2.3.sav;
report — Kristall2.3.doc

Initial data from the source:

N = 3003 kN	Shear force;
Ry = 240 MPa	Steel grade C245; Beam chord section: 530×25 mm;
Rbun = 110 kN/cm2	High strength bolts from 40H “select” steel; Diameter of bolts 24 mm, diameter of holes 27 mm;
γc = 1	Service factor;
γb = 1	Service factor of the friction connection; Method of cleaning the surfaces – flame treatment, without preservation;
μ = 0,42	Coefficient of friction;
γh = 1,12	Tightening control – by the torque.

 

KRISTALL parameters:
Steel: C245

Importance factor	1
Service factor	1
Service factor  of members to be joined	1

 

Diameter of bolts 24 mm
Steel: 40H "select"
Clearance 3 mm
Method of cleaning the surfaces to be joined: Flame treatment of two surfaces, without preservation

 

Type:	Parameters:
	m = 3 n = 3 a = 70 mm b = 125 mm c = 50 mm t = 16 mm t0 = 24 mm

 

Internal forces and moments:

N = 3003 kN
M = 0 kNm
Q = 0 kN

Manual calculation:

1. Design tension resistance of high strength bolts was calculated according to the following formula:

\[ R_{bh} =0,7R_{bun} =0,7\times 1100=770 \quad Н/мм^{2}=77,0 \quad kN/cm^{2}. \]

2. Design force which can be resisted by each plane of friction:

\[ Q_{bh} =\frac { R_{bh} A_{bn} \mu} {\gamma_{h} }=\frac {77\times 3,53\times 0,42}{1,12}=101,93 \quad kN, \]

3. Required number of bolts:

\[ n\ge \frac{N}{Q_{bh} \kappa \gamma_{b} \gamma_{c} }=\frac{3003}{101,93\times 2\times 1,0\times 1,0}=14,731. \]

Comparison of solutions:

Factor	Friction force limit
Manual calculation	14,731/16 = 0,921
KRISTALL	0,923
Deviation from the manual calculation, %	0,2
Source	0,925