Analysis of a Connection between a Bar in Tension from Two Angles and a Gusset Plate
Objective: Check the mode for calculating welded connections.
Task: Check the connection between a steel bar in tension from two equal angles and a gusset plate.
References: Moskalev N.S., Pronosin J.A. Steel Structures. Handbook / M.: ASV Publishing House, 2010. p. 83 – 84.
Compliance with the codes: SNiP II-23-81*, SP 16.13330.2011, SP 16.13330.2017, DBN B.2.6-163:2010, DBN B.2.6-198:2014.
Initial data:
| Run = 490 MPa | Steel С345 |
| Section | Angle 80х7 mm |
| t = 12 mm | Thickness of the gusset plate |
| Rwf = 215 MPa | CO2 semiautomatic welding with a Sv-08G2S wire |
| N = 700 kN | Longitudinal force |
| kf1 = 6 mm | Weld at free leg |
| kf2 = 6 mm | Weld at connected leg |
| lw1 = 22 cm | Weld length at free leg |
| lw2 = 10 cm | Weld length at connected leg |
Initial data file:
1.4.sav;
report — Kristall1.4.doc
KRISTALL initial data:
Steel: C345 category 1
|
Importance factor |
1 |
|
Service factor |
1 |
|
Group of structures according to the table 50* of SNiP II-23-81* |
1 |
|
Properties of welding materials: |
|
|---|---|
|
Characteristic resistance of the weld metal based on the ultimate strength, Rwun |
490 N/mm2 |
|
Design resistance of the fillet welds for shear in the weld metal, Rwf |
215 N/mm2
|
|
Type of welding |
Automatic and semiautomatic, diameter of the electrode wire not less than 1.4-2.0 mm |
|
Position of weld |
Flat |
|
Climatic region |
with temperature t > -40°C |
| Type: | Parameters: |
|---|---|
|
Section - Full assortment of GOST profiles.. Equal angle GOST 8509-93 L80x7 |
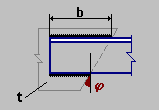
Weld at free leg = 6 mm Weld at connected leg = 6 mm b = 220 mm φ = 56.31 degrees t = 12 mm
|
Internal forces:
N = 700 kN
|
Checked according to SNiP |
Check |
Utilization factor |
|---|---|---|
|
Sec.11.2 Formula (120) |
of the weld metal |
1.036 |
|
Sec.11.2 Formula (121) |
of the metal of the fusion border |
0.902 |
Comparison of solutions
|
Check |
of the weld metal |
|
Source |
9,04 cm / 9 cm = 1,0044 21,1 cm / 21 cm = 1,0048 |
|
KRISTALL |
1,036 |
|
Deviation, % |
3,01 |
|
Refined manual calculation (see comments) |
0,72125×9,04 cm / 0,7×9 cm = 1,035 0,72125×21,1 cm / 0,7×21 cm = 1,035 |
|
Deviation, % |
0,1 |
Comments:
The distribution of the external longitudinal force between the welds along the toe and heel of the angle is not specified precisely in the verification example, i.e. the longitudinal force in the weld along the heel is given as 70% of the external longitudinal force, and that along the toe is given as 30% of the force. The exact value of the longitudinal force acting in the welds along the heel is calculated as:
(bangle – y0)/bangle×N = 0,72125×N, where bangle – angle leg width, y0 – length of a perpendicular dropped from the center of mass of the angle to the respective external leg face.