Analysis of a Welded Connection for a Bending Moment Acting in the Fillet Weld Plane
Objective: Check the mode for calculating welded connections.
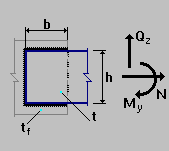
Task: Check the welded connection with fillet welds. The connection is loaded with a bending moment acting in the weld plane.
References: Moskalev N.S., Pronosin J.A. Steel Structures. Handbook / M.: ASV Publishing House, 2010. p. 88-89.
Compliance with the codes: SNiP II-23-81*, SP 16.13330.2011, SP 16.13330.2017, DBN B.2.6-163:2010, DBN B.2.6-198:2014.
Initial data:
| Run = 370 MPa | Steel С245 |
| М = 51 kNm | Force |
| l1 = 20 cm | Geometric length of longitudinal fillet welds |
| l2 = 25 cm | Geometric length of the transverse fillet weld |
| Rwf = 185 MPa | Manual welding with E46 electrodes |
| kf = 8 mm | Weld leg |
Initial data file:
1.8.sav;
report — Kristall1.8.doc
KRISTALL initial data:
Steel: C245
|
Importance factor |
1 |
|
Service factor |
1 |
|
Group of structures according to the table 50* of SNiP II-23-81* |
4 |
|
Properties of welding materials: |
|
|---|---|
|
Characteristic resistance of the weld metal based on the ultimate strength, Rwun |
450000 kN/m2 |
|
Design resistance of the fillet welds for shear in the weld metal, Rwf |
200000 kN/m2 |
|
Type of welding |
Manual |
|
Position of weld |
Flat |
|
Climatic region |
with temperature t > -40°C |
|
Type: |
Parameters: |
|---|---|
|
|
Weld leg = 8 mm
|
Internal forces and moments:
N = 0 kN
My = 51 kNm
Qz = 0 kN
|
Checked according to SNiP |
Check |
Utilization factor |
|---|---|---|
|
Sec.11.2 Formula (120) |
of the weld metal |
0.793 |
|
Sec.11.2 Formula (121) |
of the metal of the fusion border |
0.659 |
Comparison of solutions
|
Check |
of the weld metal |
of the metal of the fusion border |
|
Source |
1760 kN/cm2 / 1850 kN/cm2 = 0,951 |
1231,5 kN/cm2 / 1665 kN/cm2 = 0,740 |
|
KRISTALL |
0,793 |
0,659 |
|
Deviation, % |
16,6 |
10,95 |
|
Refined manual calculation (see comments) |
1636,178 kN/cm2 / 2000 kN/cm2 = 0,818 |
1135,787 kN/cm2 / 1665 kN/cm2 = 0,682 |
|
Deviation, % |
3,06 |
3,37 |
Comments:
The difference in the results is due to the inaccuracy made by the authors of the example in the design section of the weld. Moreover, the design resistance of the fillet welds for shear in the weld metal for the E46 electrodes was incorrectly taken in the example as Rwf = 185 MPa, while KRISTALL and design codes use the value of Rwf = 200 MPa.
|
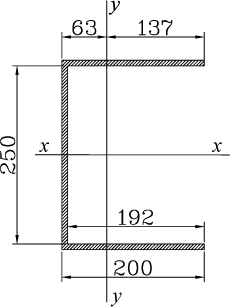
Design section of the weld |
Let’s determine the moments of inertia of the weld with respect to the principal axes of inertia for the correct design section of the weld given in the figure: \[ I_{fx} =\frac{25^{3}\cdot 0,7\cdot 0,8}{12}+\frac{\left( {0,7\cdot 0,8} \right)^{3}\cdot 20}{6}+2\cdot 0,7\cdot 0,8\cdot 20\cdot \left( {\frac{25}{2}+\frac{0,8\cdot 0,7}{2}} \right)^{2}= 4388,31 \quad cm^{4} \] \[ \begin{array}{l} I_{fy} =\frac{25\cdot \left( {0,7\cdot 0,8} \right)^{3}}{12}+25\cdot 0,7\cdot 0,8\cdot \left( {6,31-\frac{0,7\cdot 0,8}{2}} \right)^{2}+\frac{0,7\cdot 0,8\cdot 20^{3}}{6}+ \\ +2\cdot 0,7\cdot 0,8\cdot 20\cdot \left( {\frac{20}{2}-6,31} \right)^{2}=1561,086 \quad cm^{4} \\ \end{array} \] \[ I_{zx} =\frac{25^{3}\cdot 1,0\cdot 0,8}{12}+\frac{\left( {1,0\cdot 0,8} \right)^{3}\cdot 20}{6}+2\cdot 1,0\cdot 0,8\cdot 20\cdot \left( {\frac{25}{2}+\frac{0,8\cdot 1,0}{2}} \right)^{2}=6368,5 \quad cm^{4} \] \[ \begin{array}{l} I_{zy} =\frac{25\cdot \left( {1,0\cdot 0,8} \right)^{3}}{12}+25\cdot 1,0\cdot 0,8\cdot \left( {6,31-\frac{1,0\cdot 0,8}{2}} \right)^{2}+\frac{1,0\cdot 0,8\cdot 20^{3}}{6}+ \\ +2\cdot 1,0\cdot 0,8\cdot 20\cdot \left( {\frac{20}{2}-6,31} \right)^{2}=2202,01 \quad cm^{4} \\ \end{array} \] |
Then the strength checks of the weld will be as follows:
– of the weld metal:
\[ \sigma_{f} =\frac{510000}{4388,31+1561,086}\sqrt {13,3^{2}+13,69^{2}} =1636,178 \quad kN/cm^{2} < 2000 kN/cm^{2} \]
– of the metal of the fusion border:
\[ \sigma_{f} =\frac{510000}{6368,5+2202,01}\sqrt {13,3^{2}+13,69^{2}} =1135,787 \quad kN/cm^{2} < 1665 kN/cm^{2} \]