Расчет прочности и жесткости второстепенных балок для усложненного типа балочной клетки

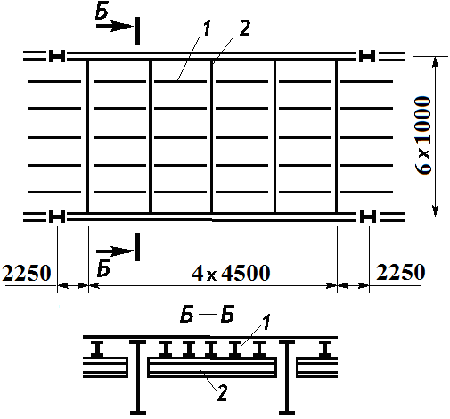
1 – балка настила
2 – второстепенная балка

Цель: Проверка режима расчета и подбора балок

Задача: Подобрать прокатный двутавровый профиль для второстепенных балок пролетом 6 м в балочной клетке усложненного типа. Верхний пояс второстепенных балок раскреплен по длине балками настила, расположенными с шагом 1 м.

Ссылки: Металлические конструкции: учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.]; под. Ред. Ю. И. Кудишина. - 13-е изд., испр. - М. : Издательский центр "Академия", 2011. С 183.

Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.

Имя файла с исходными данными:

3.3.sav;
Kristall 3.3.doc — отчет

Исходные данные:

а = 4,5 м	Шаг второстепенных балок;
q_н = (0,77 + 27,3/102 + 20) кН/м² × 4,5 м = 94,67 кН/м	Суммарная нормативная нагрузка;
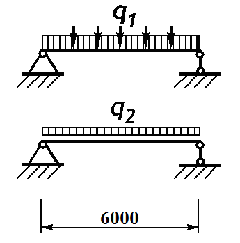
q₁= 1,05×(0,77 + 27,3/102) кН/м² × 4,5 м = 4,9 кН/м	Расчетная постоянная нагрузка;
q2 = 1,2×20 кН/м² × 4,5 м = 108 кН/м	Расчетная временная нагрузка;
R_y = 23 кН/cм²,	Сталь марки C235;
l = 6,0 м	Пролет балки;
[ f ] = 1/250×6,0 м = 24 мм	Предельный прогиб;
γ_c = 1	Коэффициент условий работы;
W_y = 2034,98 см³	Принятый двутавр №55 по ГОСТ 8239-89;
I_y = 55962 см⁴.

Параметры КРИСТАЛЛ:

Сталь: C235

Группа конструкций по таблице 50* СНиП II-23-81* 4
Коэффициент надежности по ответственности γ_n = 1
Коэффициент надежности по ответственности (2-е предельное состояние) = 1
Коэффициент условий работы 1

Конструктивное решение

Закрепления от поперечных смещений и поворотов

	Слева	Справа
Смещение вдоль Y	Закреплено	Закреплено
Смещение вдоль Z	Закреплено	Закреплено
Поворот вокруг Y
Поворот вокруг Z

Закрепления из плоскости изгиба n=6

Сечение

Профиль: Двутавp с уклоном полок по ГОСТ 8239-89 55

Ручной расчет:

1. Расчетный изгибающий момент, действующий в пролете балки:

\[ M_{\max } =\frac{q_{\Sigma } l^{2}}{8}=\frac{\left( {4,9+108} \right)\cdot 6,0^{2}}{8}=508,05 \quad кНм. \]

2. Необходимый момент сопротивления балки в предположении упругих деформаций стали:

\[ W_{nes} =\frac{M_{\max } }{R_{y} }=\frac{508,05\cdot 100}{23}=2208,913 \quad см^{3}. \]

3. Максимальный прогиб, возникающий в середине пролета балки:

\[ f_{\max } =\frac{5}{384}\cdot \frac{q_{н} l^{4}}{EI_{y} }=\frac{5}{384}\cdot \frac{94,67\cdot 6,0^{4}}{2,06\cdot 10^{5}\cdot 10^{3}\cdot 55962\cdot 10^{-8}}=13,858 \quadмм. \]

4. Условная предельная гибкость сжатого пояса балки:

\[ \bar{{\lambda }}_{ub} =0,35+0,0032\frac{b_{f} }{t_{f} }+\left( {0,76-0,02\frac{b_{f} }{t_{f} }} \right)\frac{b_{f} }{h_{f} }=0,35+0,0032\frac{180}{16,5}+\left( {0,76-0,02\frac{180}{16,5}} \right)\frac{180}{533,5}=0,5677. \]

5. Условная фактическая гибкость сжатого пояса балки:

\( \bar{{\lambda }}_{b} =\frac{l_{ef} }{b_{f} }\sqrt {\frac{R_{y} }{E}} =\frac{1000}{180}\sqrt {\frac{230}{2,06\cdot 10^{5}}} =0,1856<\bar{{\lambda }}_{ub} =0,5677 \) – проверка устойчивости не требуется.

Сравнение решений:

Фактор	Прочность при действии поперечной силы	Прочность при действии изгибающего момента	Устойчивость плоской формы изгиба при действии момента	Максимальный прогиб
Ручной счет	–	2208,913/2034,98 =1,085	–	13,858/24 = 0,577
КРИСТАЛЛ	0,488	1,085	1,085	13,856/24 = 0,577
Отклонение от ручного счета, %	0,0	0,0	0,0	0,0
Источник	–	0,99	–	0,58

Комментарии:

Проверка касательных напряжений при ручном счете не выполнялась из-за отсутствия ослаблений и относительно большой толщины стенок балки.
Проверка прочности при действии изгибающего момента в источнике выполнялась с учетом развития ограниченных пластических деформаций.
Проверка прочности балки с учетом развития ограниченных пластических деформаций не выполнялась, поскольку согласно норм такой расчет возможен только при соответствующем оребрении стенки балки. В исходных данных примера для второстепенной балки подбиралась прокатная балка без промежуточных ребер жесткости.