Расчет сквозной центрально-сжатой колонны из двух сплошностенчатых ветвей швеллерного сечения на планках

Цель: Проверка режима расчета сопротивления сечений

Задача: Проверить расчетное сквозное сечение на планках с двумя сплошностенчатыми ветвями из прокатных швеллеров для центрально-сжатой колонны высотой 6 м.

Источник: Металлические конструкции: учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.]; под. Ред. Ю. И. Кудишина. - 13-е изд., испр. - М. : Издательский центр "Академия", 2011. С 257.

Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.

Имя файла с исходными данными:

4.7.sav;
отчет — Kristall-4.7.doc

Исходные данные:

l = 6 м	Высота колонны;
μ = 1	Закрепление шарнирное в обеих плоскостях инерции;
N = 1400 кН	Расчетное усилие сжатия;
γ_c = 1	Коэффициент условий работы;
R_y = 24 кН/cм²	Сталь марки C245;
В = 300 мм	Расстояние между ветвями (габарит по внешним граням);
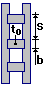
b = 170 мм, s = 1120 мм	Высота планки, расстояние между осями планок;
t = 10 мм	Толщина планок;
A = 70,4 см², I_y = 8320 см⁴, I_z = 11576,86 см⁴ i_y = 10,871 см, i_z = 12,824 см	Геометрические характеристики сквозного сечения;
A_b = 35,2 см², I_b = I_z = 262 см⁴, i_y = 10,871 см, i_z = 2,728 см W_b,z,min = 37,269 см³.	Геометрические характеристики сечения ветви;

Параметры КРИСТАЛЛ:

Сталь: C245

Группа конструкций по таблице 50* СНиП II-23-81* 3
Коэффициент надежности по ответственности 1
Коэффициент условий работы 1
Предельная гибкость для сжатых элементов: 180 - 60α
Предельная гибкость для растянутых элементов: 250

Сечение

Профиль: Швеллеp с уклоном полок по ГОСТ 8240-89 27

Решетка

b = 170 мм
t₀ = 10 мм
s = 1120 мм

Ручной расчет (СНиП II-23-81*):

1. Момент инерции и момент сопротивления сечения одной планки относительно собственной оси:

\[ I_{s} =\frac{t_{0} b^{3}}{12}=\frac{1\cdot 17^{3}}{12}=409,4167 \quad см^{4}; \] \[ W_{s} =\frac{t_{0} b^{2}}{6}=\frac{1\cdot 17^{2}}{6}=48,167 \quad см^{3}. \]

2. Расстояние между осями ветвей:

\[ b=B-2z_{0} =30-2\cdot 2,47=25,06 \quad см. \]

3. Гибкости одной из веток на участках между планками (в свету):

\[ \lambda_{1,y} =\frac{l_{1,y} }{i_{1,y} }=\frac{600}{10,871}=55,193; \quad \bar{{\lambda }}_{1,y} =\lambda_{1,y} \sqrt {\frac{R_{y} }{E}} =55,193\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,884\le 5; \] \[ \lambda_{1,z} =\frac{l_{1,z} }{i_{1,z} }=\frac{s-b}{i_{1,z} }=\frac{112-17}{2,728}=34,824<40; \quad \bar{{\lambda }}_{1,z} =\lambda_{1,z} \sqrt {\frac{R_{y} }{E}} =34,824\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,1886\le 5. \]

4. Гибкости колонны и соответствующие условные гибкости:

\[ \lambda_{y} =\frac{l_{ef,y} }{i_{y} }=\frac{600}{10,871}=55,193; \quad \Rightarrow \quad \bar{{\lambda }}_{y} =\lambda_{y} \sqrt {\frac{R_{y} }{E}} =55,193\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,884<2,5; \] \[ \lambda_{z} =\frac{l_{ef,z} }{i_{z} }=\frac{600}{12,824}=46,787. \]

5. Приведенная и условная приведенная гибкости колонны относительно свободной оси:

При \( \frac{I_{s} s}{I_{b} b}=\frac{409,4167\cdot 112}{262\cdot 25,06}=6,984>5: \)

\[ \lambda_{z} =\lambda_{ef,z} =\sqrt {\lambda_{z}^{2} +\lambda_{1,z}^{2} } =\sqrt {46,787^{2}+34,824^{2}} =58,3244; \] \[ \bar{{\lambda }}_{z} =\lambda_{z} \sqrt {\frac{R_{y} }{E}} =58,3244\sqrt {\frac{240}{2,06\cdot 10^{5}}} =1,991<2,5. \]

6. Коэффициенты продольного изгиба:

\[ \varphi_{y} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{y} \sqrt {\bar{{\lambda }}_{y} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)\cdot 1,884\sqrt {1,884} =0,8279; \] \[ \varphi_{z} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{z} \sqrt {\bar{{\lambda }}_{z} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)\cdot 1,991\sqrt {1,991} =0,813. \]

7. Предельные сжимающие усилия, при которых происходит потеря устойчивости колонны относительно соответствующих осей:

\[ N_{b,y} =\varphi_{y} AR_{y} \gamma_{c} =0,8279\cdot 70,4\cdot 24\cdot 1=1398,82 \quad кН; \] \[ N_{b,z} =\varphi_{z} AR_{y} \gamma_{c} =0,813\cdot 70,4\cdot 24\cdot 1=1373,645 \quad кН. \]

8. Условная поперечная сила Q_fic:

\[ Q_{fic} =7,15\cdot 10^{-6}\left( {2330-\frac{E}{R_{y} }} \right)\frac{N}{\varphi_{z} }=7,15\cdot 10^{-6}\left( {2330-\frac{2,06\cdot 10^{5}}{240}} \right)\frac{1400}{0,813}=18,1198 \quad кН. \]

9. Сила F, срезывающая планку, и момент M₁, изгибающий планку в ее плоскости:

\[ F=\frac{Q_{s} s}{b}=\frac{Q_{fic} s}{2b}=\frac{18,1198\cdot 112}{2\cdot 25,06}=40,4912 \quad кН; \] \[ M_{1} =\frac{Q_{s} s}{2}=\frac{Q_{fic} s}{4}=\frac{18,1198\cdot 112}{4}=507,3544 \quad кНсм. \]

10. Несущая способность планки при изгибе:

\[ W_{s} R_{y} \gamma_{c} =48,167\cdot 24\cdot 1=1156,01 \quad кНсм. \]

11. Изгибающий момент, действующий на ветвь колонны и обусловленный изгибом планки:

\[ M_{b} =2M_{1} =2\cdot 507,3544=1014,7088 \quad кНсм. \]

12. Несущая способность ветви при изгибе в плоскости планок:

\[ W_{b,z,\min } R_{y} \gamma_{c} =37,269\cdot 24\cdot 1=894,456 \quad кНсм. \]

13. Прочность ветви при совместном действии продольной силы и изгибающего момента в плоскости планок без учета пластики:

\[ \frac{1}{R_{y} \gamma_{c} }\left( {\frac{N}{A}+\frac{M_{b} }{W_{b,z,\min } }} \right)=\frac{1}{24\cdot 1}\left( {\frac{1400}{70,4}+\frac{1014,7088}{37,269}} \right)=1,963. \]

14. Коэффициенты продольного изгиба для ветки:

\[ \varphi_{y} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{1,y} \sqrt {\bar{{\lambda }}_{1,y} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)1,884\sqrt {1,884} =0,828; \] \[ \varphi_{z} =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\lambda_{1,z} \sqrt {\lambda_{1,z} } =1-\left( {0,073-5,53\frac{240}{2,06\cdot 10^{5}}} \right)\cdot 1,1886\sqrt {1,1886} =0,914. \]

15. Несущая способность ветви при сжатии:

\[ \varphi_{y} AR_{y} \gamma_{c} =0,828\cdot 35,2\cdot 24\cdot 1=699,398 \quad кН; \] \[ \varphi_{z} AR_{y} \gamma_{c} =0,914\cdot 35,2\cdot 24\cdot 1=772,1472 \quad кН. \]

16. Относительный эксцентриситет, коэффициент влияния формы сечения, приведенный эксцентриситет и коэффициент продольного изгиба при внецентренном сжатии для ветви:

\[ m_{z} =\frac{M_{z} }{N}\cdot \frac{A_{b} }{W_{b,z,\min } }=\frac{1014,7088}{700}\cdot \frac{35,2}{37,269}=1,36911\le 5; \] \[ \frac{A_{f} }{A_{w} }=\frac{16,2}{19,95}=0,812; \] \[ \eta =\left( {1,25-0,05m_{z} } \right)-0,01\left( {5-m_{z} } \right)\bar{{\lambda }}_{1,z} =\left( {1,25-0,05\cdot 1,36911} \right)-0,01\left( {5-1,36911} \right)\cdot 1,1886=1,13838 \]

(для типа сечения 9 по табл.~73 СНиП~ІІ-23-81* при \( \frac{A_{f} }{A_{w} }=0,5);\)

\[ \eta =\left( {1,5-0,1m_{z} } \right)-0,02\left( {5-m_{z} } \right)\bar{{\lambda }}_{1,z} =\left( {1,5-0,1\cdot 1,36911} \right)-0,02\left( {5-1,36911} \right)\cdot 1,1886=1,27678 \]

(для типа сечения 9 по табл.~73 СНиП~ІІ-23-81* при \( \frac{A_{f} }{A_{w} }=1,0);\)

\( \eta =1,2247 \) (для типа сечения 9 по табл.~73 СНиП~ІІ-23-81* при \( \frac{A_{f} }{A_{w} }=0,812); \)

\( \eta =1,45+0,04m_{z} =1,45+0,04\cdot 1,36911=1,50476 \) (для типа сечения 11 по табл.~73 СНиП~ІІ-23-81* при \( \frac{A_{f} }{A_{w} }=0,5); \)

\( \eta =1,8+0,12m_{z} =1,8+0,12\cdot 1,36911=1,9643 \) (для типа сечения 11 по табл.~73 СНиП~ІІ-23-81* при \( \frac{A_{f} }{A_{w} }=1,0); \)

\( \eta =1,7915 \) (для типа сечения 11 по табл.~73 СНиП~ІІ-23-81* при \( \frac{A_{f} }{A_{w} }=1,33811); \)

\[ m_{z,ef} =\eta m_{z} =1,7915\cdot 1,36911=2,453; \]

\( \varphi_{e} =0,4174 \) (по табл.~74 СНиП~ІІ-23-81*).

17. Проверка устойчивости ветви в плоскости изгиба планок:

\[ \frac{N}{2\varphi_{e} A_{b} }=\frac{1400}{2\cdot 0,4174\cdot 35,2}=47,6434 \quad кН/см^{2} \quad >R_{y} \gamma_{c} =24\cdot 1=24 \quad кН/см^{2}. \]

18. Проверка устойчивости ветви из плоскости изгиба планок производится как проверка устойчивости центрально-сжатого стержня в соответствующей плоскости согласно п. 5.32 СНиП II-23-81*.

Сравнение решений:

Фактор	Источник	Ручной счет	КРИСТАЛЛ
Общая устойчивость стержня при центральном сжатии в плоскости XoY	24/24=1	1400/1373,645 = 1,019	1,019
Общая устойчивость стержня при центральном сжатии в плоскости XoZ	23,6/24=0,983	1400/1398,82 = 1,001	1,001
Сопротивление соединительной планки изгибу	–	507,3544/1156,01 = 0,439	0,439
Прочность ветви при действии изгибающего момента Mz	–	1014,7088/894,456 = 1,134	1,134
Прочность ветви при совместном действии продольной силы и изгибающих моментов без учета пластики	–	1,963	1,963
Устойчивость ветви при сжатии в плоскости XoY	–	700/772,1472 = 0,9066	0,907
Устойчивость ветви при сжатии в плоскости XoZ	23,6/24=0,983	700/699,398 = 1,001	1,001
Устойчивость ветви в плоскости действия момента Mz при внецентренном сжатии	–	47,6434/24 = 1,985	1,985
Устойчивость ветви из плоскости действия момента Mz при внецентренном сжатии	–	24,01735/24 = 1,001	1,001
Предельная гибкость в плоскости XoY	–	58,3244/120 = 0,486	0,486
Предельная гибкость в плоскости XoZ	–	55,193/120 = 0,46	0,46