Circular Tunnel Lining Subjected to the Given Active Vertical And Horizontal Earth Pressure and Passive Lateral Earth Pressure in the Contact Area

Objective: Determination of the internal forces in the structure of a circular tunnel lining and the elastic reactions of soil in the contact area from the action of the given vertical and horizontal earth pressure in the structurally nonlinear formulation.

Initial data file: Tunnel_lining.spr

Problem formulation: The circular tunnel lining is subjected to the action of the given active vertical p and horizontal q arching earth pressure and passive lateral earth pressure in the contact area. Determine the internal forces (longitudinal forces N and bending moments M) in the structure of the circular tunnel lining and the elastic reactions of soil R in the contact area.

References: M.M. Archangelsky, D.I. Jincharadze, A.S. Kurisko, Calculation of Tunnel Lining, Moscow, TRANSZHELDORIZDAT, 1960, p. 217

Initial data:

E = 3.4·106 t/m2	- elastic modulus of the tunnel lining material;
γb = 2.6 t/m3	- specific weight of the tunnel lining material;
dint = 7.1 m	- inner diameter of the tunnel lining ring;
h = 0.4	- thickness of the rectangular cross-section of the tunnel lining;
b = 1.0	- width of the rectangular cross-section of the tunnel lining;
α = π/8 rad	- central angle of the side of the regular polygon of the frame replacing the circle of the design radius r of the tunnel lining;
k = 5.0·103 t/m3	- coefficient of lateral earth pressure in the area of contact with the tunnel lining;
f = 0.8	- Protodyakonov hardness coefficient;
φ = 2·π/9 rad	- angle of internal friction of soil;
γg = 1.9 t/m3	- specific weight of soil.
dext = dint + 2·h = 7.9 m	- outer diameter of the tunnel lining ring;
r = (dext + dint)/4 = 3.75 m	- design radius of the tunnel lining;
S = 2·r·sin(0.5·α) = 1.463177 m	- side of the regular polygon of the replacement frame;
I = b·h3/12 = 0.005333 m4	- cross-sectional moment of inertia of the tunnel lining;
F = b·h = 0.4 m2	- cross-sectional area of the tunnel lining;
D = k·S·b = 7315.887 t/m	- stiffness of the elastic supports modeling the lateral earth pressure and radially arranged at the vertices of the polygon of the replacement frame;
Larch = dext·(1+ tg(π/4 – φ/2)) = 11.584 m	- span of the earth pressure arch;
Harch = Larch/(2·f) = 7.240 m	- height of the earth pressure arch above the excavation;
p = Harch·γg + h· γb =14.796 t/m2	- vertical uniformly distributed active earth pressure;
q = (Harch + dext/2)· γg·tg2(π/4 – φ/2) = 4.623 t/m2	- horizontal uniformly distributed active earth pressure.

 

Vertical concentrated forces in the nodes of the polygon of the frame replacing the distributed load

P₁ = (S/2)∙p∙(cos(– 0.5∙α) + cos(0.5∙α)) = 21.2329 t;

P₂ = (S/2)∙p∙(cos(0.5∙α) + cos(1.5∙α)) = 19.6166 t;

P₃ = (S/2)∙p∙(cos(1.5∙α) + cos(2.5∙α)) = 15.0139 t;

P₄ = (S/2)∙p∙(cos(2.5∙α) + cos(3.5∙α)) = 8.1255 t;

P₅ = (S/2)∙p∙cos(3.5∙α) = 2.1117 t.

 

Horizontal concentrated forces in the nodes of the polygon of the frame replacing the distributed load

Q₁ = (S/2)∙q∙sin(0.5∙α) = 0.6598 t;

Q₂ = (S/2)∙q∙(sin(0.5∙α) + sin(1.5∙α)) = 2.5388 t;

Q₃ = (S/2)∙q∙(sin(1.5∙α) + sin(2.5∙α)) = 4.6911 t;

Q₄ = (S/2)∙q∙sin(2.5∙α) =2.8121 t.

 

Finite element model: Design model – general type system. Elements of the tunnel lining – 16 bar elements of type 5. The tunnel lining is divided into finite elements along the circle of radius r = 3.75 m, lying in the XOZ plane of the global coordinate system by the step of the central angle of α = π/8 rad. The origin of the global coordinate system is in the center of the circle. The X₁ axes of the local coordinate systems of the elements are directed along the chords of the circle in the clockwise direction around the Y axis of the global coordinate system when viewed from the origin. The Z₁ axes of the local coordinate systems of the elements are directed from the center of the circle. Elements modeling the lateral earth pressure – 16 two-node elements of unilateral constraints working in compression of type 352. Finite elements are directed along the radii of the circle from the center and are adjacent to the nodes between the elements of the tunnel lining. Boundary conditions are provided by imposing constraints on the support nodes of the elements modeling the lateral earth pressure in the directions of the degrees of freedom X, Y, Z, and on the elements of the tunnel lining in the direction of the degree of freedom Y. The dimensional stability of the design model is provided by imposing constraints in the direction of the degree of freedom X on the nodes of the elements of the tunnel lining located along the vertical axis of symmetry. The action of the active vertical and horizontal earth pressure is specified as vertical P_i and horizontal Q_i concentrated forces in the nodes between the elements of the tunnel lining. The nonlinear loading was generated by the simple incremental method with a loading factor – 0.01 and a number of steps – 100 for the linear loading. Number of nodes in the design model – 32.

 

Results in SCAD

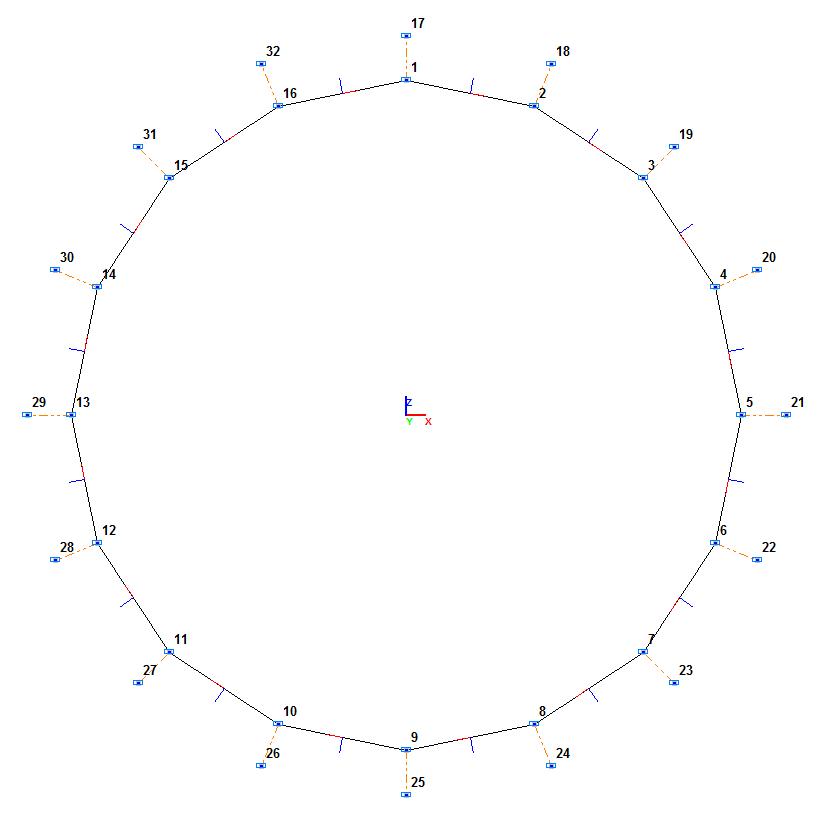
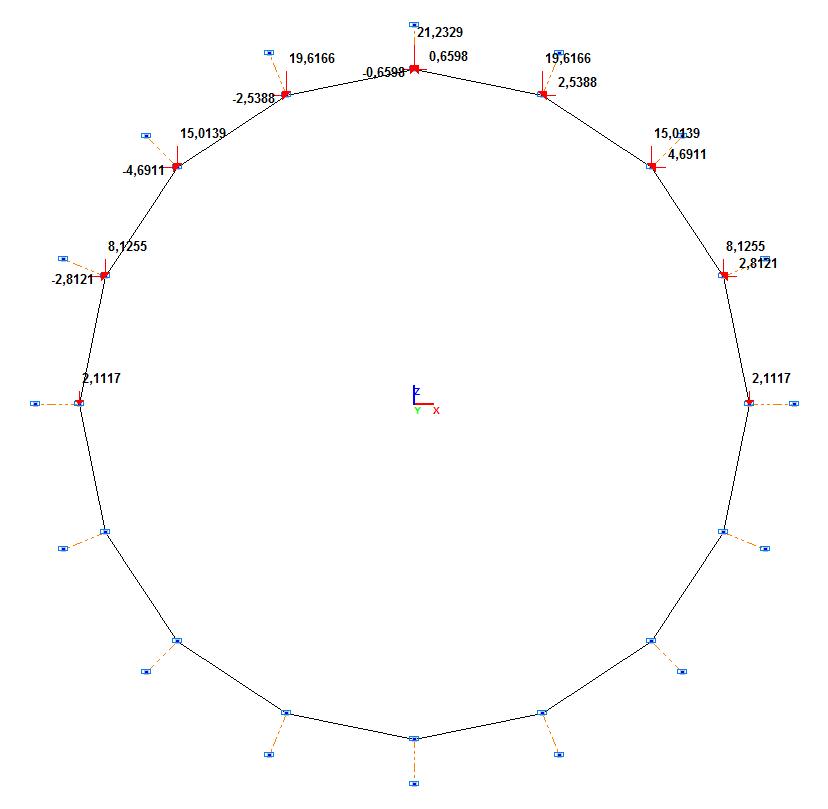
Design model

 

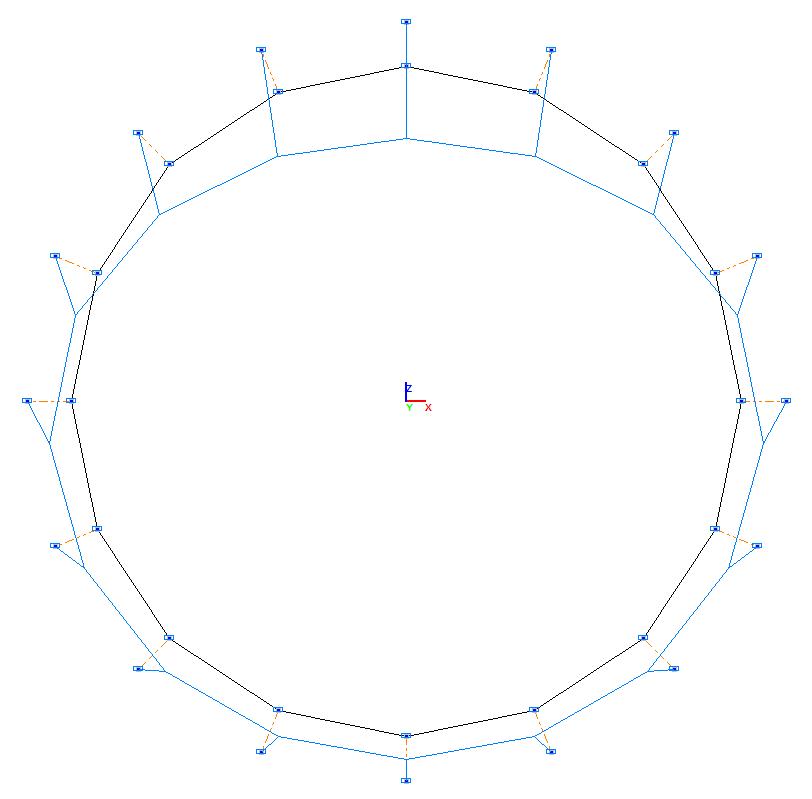
Deformed model

 

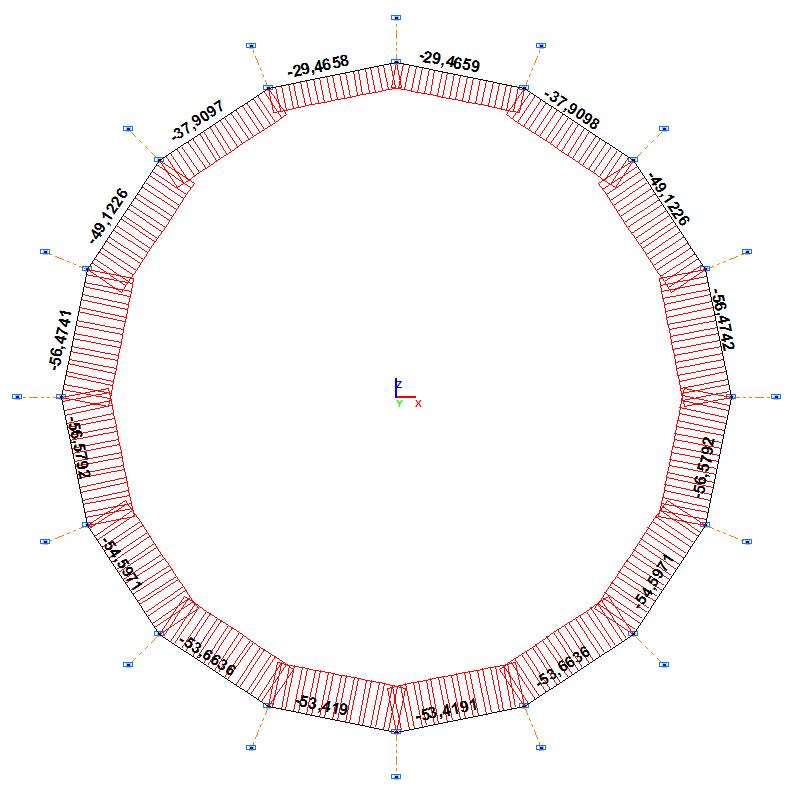
Longitudinal force diagram N, т

 

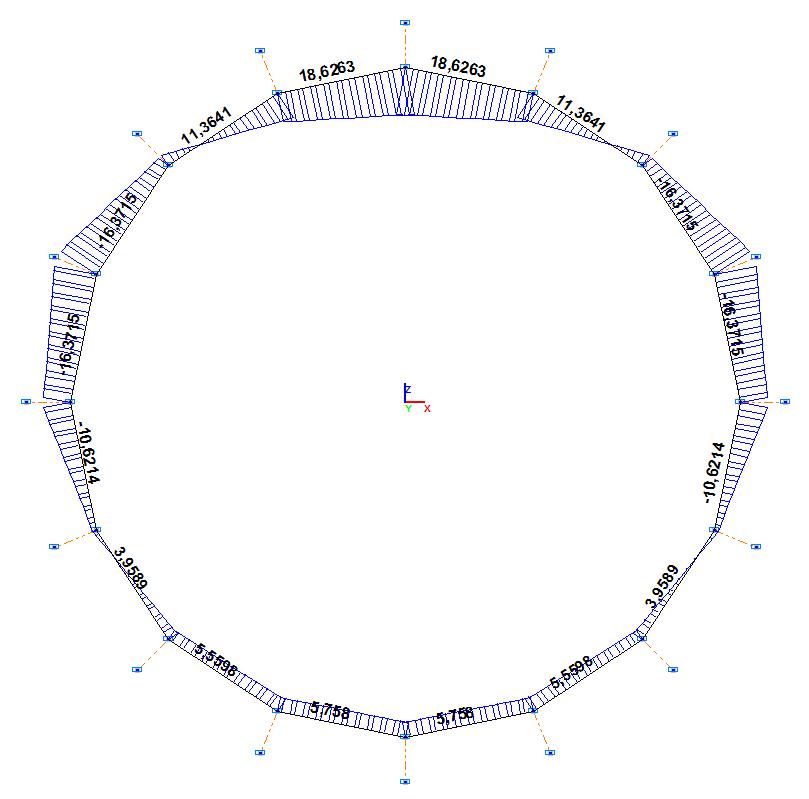
Bending moment diagram M, t∙m

 

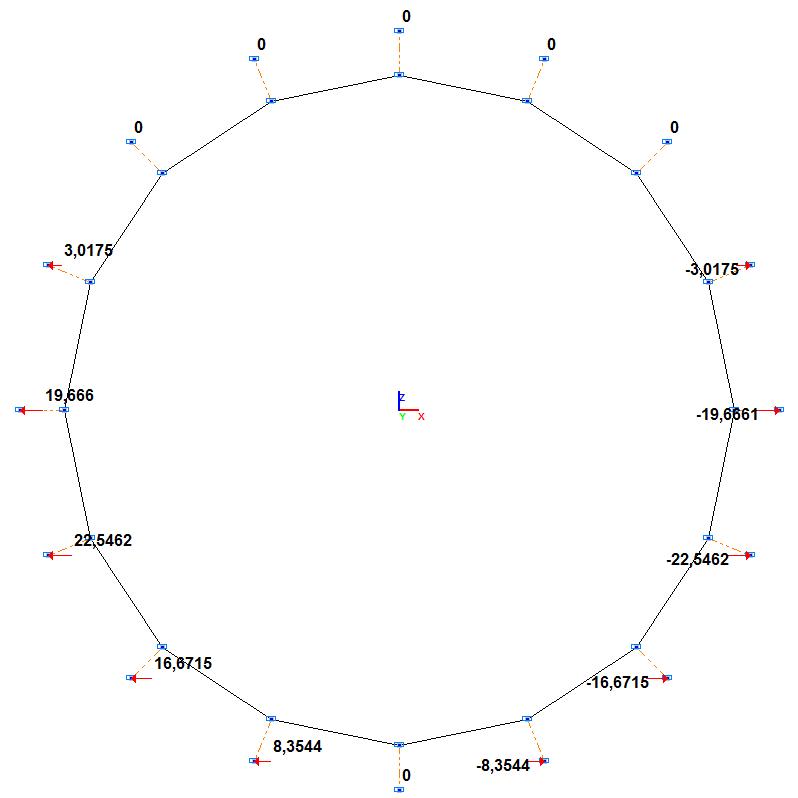
Values of reactions in the support nodes along the X axis of the global coordinate system R_x, т

 

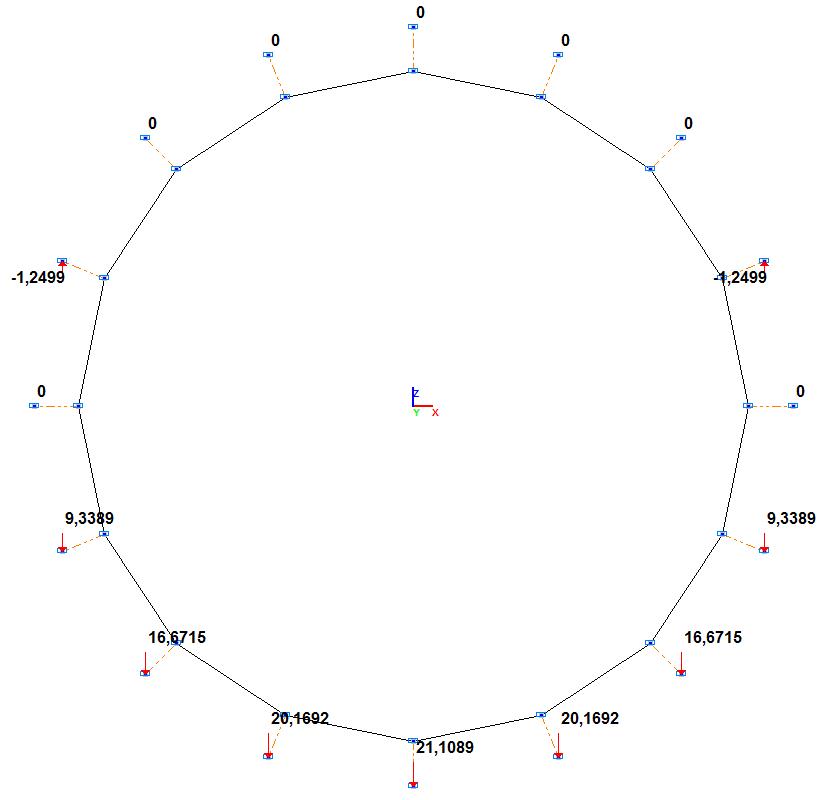
Values of reactions in the support nodes along the Z axis of the global coordinate system R_z, т

 

Comparison of solutions:

Parameter	Theory	SCAD	Deviation, %
N12, t	-29.4660	-29.4659	0.00
N23, t	-37.9098	-37.9098	0.00
N34, t	-49.1226	-49.1226	0.00
N45, t	-56.4742	-56.4742	0.00
N56, t	-56.5793	-56.5792	0.00
N67, t	-54.5971	-54.5971	0.00
N78, t	-53.6637	-53.6636	0.00
N89, t	-53.4191	-53.4191	0.00
M1, t∙m	18.6263	18.6263	0.00
M2, t∙m	11.3641	11.3641	0.00
M3, t∙m	-4.7755	-4.7755	0.00
M4, t∙m	-16.3715	-16.3715	0.00
M5, t∙m	-10.6215	-10.6214	0.00
M6, t∙m	-1.3066	-1.3065	0.01
M7, t∙m	3.9589	3.9589	0.00
M8, t∙m	5.5598	5.5598	0.00
M9, t∙m	5.7581	5.7580	0.00
R1, t	0.0000	0.0000	0.00
R2, t	0.0000	0.0000	0.00
R3, t	0.0000	0.0000	0.00
R4, t	-3.2661	-3.0175∙cos(π/8) - 1.2499∙sin(π/8) = -3.2661	0.00
R5, t	-19.6660	-19.6661	0.00
R6, t	-24.4038	-22.5462∙cos(π/8) - 9.3389∙sin(π/8) = -24.4038	0.00
R7, t	-23.5771	-16.6715∙cos(π/4) – 16.6715∙sin(π/4) = -23.5770	0.00
R8, t	-21.8310	-8.3544∙cos(3∙π/8) - 20.1692∙sin(3∙π/8) = -21.8310	0.00
R9, t	-21.1089	-21.1089	0.00

Notes: The method of calculating tunnel linings proposed by the Metroproject, which takes into account the dependence of the stress state of the structure on the elastic properties of the continuum, is used in the analytical solution. The calculation procedure is as follows:

• The area of contact of the structure with the soil is specified; the circular contour of the lining is replaced by a regular polygon; all the active loads reduced to the nodal ones and the necessary geometric properties are calculated.
• The assumed primary system of the force method has the form of a polygon with hinges in all nodes with elastic supports, and also in the central angle of the detachment area, and as a result the upper part of the polygon turns into a three-hinged arch; moments which have to be applied in the hinges to eliminate the possibility of the relative rotation of the sides of the polygon are taken as the unknowns; unit moments are applied in all hinges (the action of the pairs of unknowns acting in the symmetric nodes is considered for a symmetric system); forces in the elements of the hinged chain and reactions of the elastic supports in all unit states are determined by successively cutting out the nodes and projecting forces in the directions of the bars, and on the bisector of the angle.
• The upper part of the polygon in the detachment area is considered as a three-hinged arch, and its support vertical and horizontal pressures from the external load on the rest of the hinged polygon are determined; forces for all elements of the hinged chain and reactions of the elastic supports caused by the support forces and the active loads applied in other nodes are determined by successively cutting out the nodes.
• The unit and loading displacements are determined by the Maxwell-Mohr formulas using the approximate summation methods.
• A system of canonical equations is compiled and solved using the Gauss algorithm in order to determine the redundants.
• The longitudinal forces, bending moments and reactions of the elastic constraints are determined.
• The correctness of the specification of the contact area between the structure and the soil is checked based on the values of the reactions of the elastic supports.

The formulas for the calculation are given below.

 

Primary system of the force method

 

 

Determination of forces in the primary system from the external loads

Determination of forces in the three-hinged arch from the vertical loads

 

Design model for the determination of forces in the three-hinged arch from the vertical loads

 \[ {\begin{array}{*{20}c} {L_{1} =r\cdot \sin \left( {3\cdot \alpha } \right)} & {L_{2} =r\cdot \sin \left( \alpha \right)} & {L_{3} =r\cdot \sin \left( {2\cdot \alpha } \right)} \\ {F_{1} =r\cdot \left( {1-\cos \left( {3\cdot \alpha } \right)} \right)} & {F_{2} =r\cdot \left( {\cos \left( \alpha \right)-\cos \left( {3\cdot \alpha } \right)} \right)} & {F_{3} =r\cdot \left( {\cos \left( {2\cdot \alpha } \right)-\cos \left( {3\cdot \alpha } \right)} \right)} \\ \end{array} } \] \[ V=0.5\cdot P_{1} +P_{2} +P_{3} \quad H=\frac{V\cdot L_{1} -P_{2} \cdot L_{2} -P_{3} \cdot L_{3} }{F_{1} } \] \[ M_{3p} =V\cdot \left( {L_{1} -L_{3} } \right)-H\cdot F_{3} \quad M_{2p} =V\cdot \left( {L_{1} -L_{3} } \right)-H\cdot F_{2} -P_{3} \cdot \left( {L_{3} -L_{2} } \right) \] \[ N_{12p} =H\cdot \cos \left( {0.5\cdot \alpha } \right)+\frac{P_{1} }{2}\cdot \sin \left( {0.5\cdot \alpha } \right) \quad N_{23p} =H\cdot \cos \left( {1.5\cdot \alpha } \right)+\left( {\frac{P_{1} }{2}+P_{2} } \right)\cdot \sin \left( {1.5\cdot \alpha } \right) \] \[ N_{34p} =H\cdot \cos \left( {2.5\cdot \alpha } \right)+\left( {\frac{P_{1} }{2}+P_{2} +P_{3} } \right)\cdot \sin \left( {2.5\cdot \alpha } \right) \]

Determination of forces in the hinged chain from the vertical loads

Design model for the determination of forces in the hinged chain from the vertical loads

 \[ N_{45p} =\frac{\left( {V+P_{4} } \right)\cdot \sin \left( {3\cdot \alpha } \right)+H\cdot \sin \left( \alpha \right)}{\cos \left( {0.5\cdot \alpha } \right)}; \quad N_{56p} =N_{45p} +\frac{P_{5} }{\cos \left( {0.5\cdot \alpha } \right)}; \] \[ N_{67p} =N_{78p} =N_{89p} =N_{56p} ; \] \[ R_{4p} =H\cdot \cos \left( \alpha \right)+N_{45p} \cdot \sin \left( {0.5\cdot \alpha } \right)-\left( {V+P_{4} } \right)\cdot \cos \left( {3\cdot \alpha } \right); \] \[ R_{5p} =\left( {N_{45p} +N_{56p} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{6p} =\left( {N_{56p} +N_{67p} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \] \[ R_{7p} =R_{8p} =R_{9p} =R_{6p} . \]

Determination of forces in the three-hinged arch from the horizontal loads

\[ H_{cr} =\frac{Q_{1} \cdot F_{1} +Q_{2} \cdot F_{2} +Q_{3} \cdot F_{3} }{F_{1} }\quad ; \quad H_{sk} =\frac{Q_{2} \cdot \left( {F_{1} -F_{2} } \right)+Q_{3} \cdot \left( {F_{1} -F_{3} } \right)}{F_{1} }; \] \[ M_{2q} =\left( {H_{cr} -Q_{1} } \right)\cdot \left( {F_{1} -F_{2} } \right); \quad M_{3q} =H_{sk} \cdot F_{3} ; \] \[ N_{12q} =\left( {H_{cr} -Q_{1} } \right)\cdot \cos \left( {0.5\cdot \alpha } \right); \quad N_{23q} =\left( {H_{cr} -Q_{1} -Q_{2} } \right)\cdot \cos \left( {1.5\cdot \alpha } \right); \]

Determination of forces in the hinged chain from the horizontal loads

\[ N_{45q} =-\frac{\left( {H_{sk} +Q_{4} } \right)\cdot \cos \left( {3\cdot \alpha } \right)}{\cos \left( {0.5\cdot \alpha } \right)}\quad ; \quad N_{56q} =N_{67q} =N_{78q} =N_{89q} =N_{45q} ; \] \[ R_{4q} =-\left( {H_{sk} +Q_{4} } \right)\cdot \sin \left( {3\cdot \alpha } \right)+N_{45q} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{5q} =\left( {N_{45q} +N_{56q} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \] \[ R_{6q} =R_{7q} =R_{8q} =R_{9q} =R_{5q} . \]

 Determination of forces in the primary system from the unit moments

Determination of forces in the three-hinged arch from the unit moment applied in the point 1

\[ M_{11} =1\quad ; \quad H_{1} =\frac{M_{11} }{F_{1} }; \] \[ M_{21} =H_{1} \cdot F_{2} ; \quad M_{31} =H_{1} \cdot F_{3} ; \] \[ N_{121} =-H_{1} \cdot \cos \left( {0.5\cdot \alpha } \right); \quad N_{231} =-H_{1} \cdot \cos \left( {1.5\cdot \alpha } \right); \quad N_{341} =-H_{1} \cdot \cos \left( {2.5\cdot \alpha } \right). \]

Determination of forces in the hinged chain from the unit moment applied in the point 1

\[ N_{451} =-\frac{H_{1} \cdot \sin \left( \alpha \right)}{\cos \left( {0.5\cdot \alpha } \right)}; \quad N_{561} =N_{671} =N_{781} =N_{891} =N_{451} ; \] \[ R_{41} =N_{451} \cdot \sin \left( {0.5\cdot \alpha } \right)-H_{1} \cdot \cos \left( \alpha \right); \quad R_{51} =2\cdot N_{451} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{61} =R_{71} =R_{81} =R_{91} =R_{51} . \]

Determination of forces in the three-hinged arch from the unit moment applied in the point 4

\[ M_{44} =1\quad ; \quad H_{4} =\frac{M_{44} }{F_{1} }; \] \[ M_{24} =M_{44} -H_{4} \cdot F_{2} ; \quad M_{34} =M_{44} -H_{4} \cdot F_{3} ; \] \[ N_{124} =H_{4} \cdot \cos \left( {0.5\cdot \alpha } \right); \quad N_{234} =H_{4} \cdot \cos \left( {1.5\cdot \alpha } \right); \quad N_{344} =H_{4} \cdot \cos \left( {2.5\cdot \alpha } \right). \]

Determination of forces in the hinged chain from the unit moment applied in the point 4

\[ N_{454} =\frac{H_{4} \cdot \sin \left( \alpha \right)}{\cos \left( {0.5\cdot \alpha } \right)}+\frac{M_{44} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{564} =N_{454} +\frac{M_{44} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \] \[ N_{674} =N_{784} =N_{894} =N_{564} ; \] \[ R_{41} =N_{451} \cdot \sin \left( {0.5\cdot \alpha } \right)+H_{4} \cdot \cos \left( \alpha \right)+\frac{M_{44} \cdot \cos \left( \alpha \right)}{S}; R_{51} =-\frac{M_{44} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+\left( {N_{454} +N_{564} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \] \[ R_{64} =2\cdot N_{564} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{74} =R_{84} =R_{94} =R_{64} . \]

Determination of forces in the hinged chain from the unit moment applied in the point 5

\[ M_{55} =1; \] \[ N_{455} =-\frac{M_{55} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{565} =N_{455} ; \] \[ R_{45} =-\frac{M_{55} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{55} =\frac{2\cdot M_{55} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{455} \cdot \sin \left( {0.5\cdot \alpha } \right); R_{65} =-\frac{M_{55} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \]

Determination of forces in the hinged chain from the unit moment applied in the point 6

\[ M_{66} =1; \] \[ N_{566} =-\frac{M_{66} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{676} =N_{566} ; \] \[ R_{56} =-\frac{M_{66} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{66} =\frac{2\cdot M_{66} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{566} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{76} =-\frac{M_{66} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \]

Determination of forces in the hinged chain from the unit moment applied in the point 7

\[ M_{77} =1; \] \[ N_{677} =-\frac{M_{77} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{787} =N_{677} ; \] \[ R_{67} =-\frac{M_{77} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{77} =\frac{2\cdot M_{77} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{677} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{87} =-\frac{M_{77} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \]

Determination of forces in the hinged chain from the unit moment applied in the point 8

\[ M_{88} =1; \] \[ N_{788} =-\frac{M_{88} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{898} =N_{788} ; \] \[ R_{78} =-\frac{M_{88} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{88} =\frac{2\cdot M_{88} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{788} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{98} =-\frac{2\cdot M_{88} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \]

Determination of forces in the hinged chain from the unit moment applied in the point 9

\[ M_{99} =1; \] \[ N_{899} =-\frac{M_{99} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \] \[ R_{89} =-\frac{M_{99} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{99} =\frac{2\cdot M_{99} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{899} \cdot \sin \left( {0.5\cdot \alpha } \right). \]

Determination of displacements

\[ \delta_{11R} =2\cdot \frac{1}{D}\cdot \left( {R_{41}^{2}+R_{51} ^{2}+R_{61}^{2}+R_{71}^{2}+R_{81}^{2}+R_{91}^{2}\cdot 0.5} \right); \] \[ \delta_{11M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot \left( {M_{11} ^{2}+M_{11} \cdot M_{21} +2\cdot M_{21}^{2}+M_{21} \cdot M_{31} +2\cdot M_{31}^{2}} \right); \] \[ \delta_{11N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{121}^{2}+N_{231} ^{2}+N_{341}^{2}+N_{451}^{2}+N_{561}^{2}+N_{671}^{2}+N_{781} ^{2}+N_{891}^{2}} \right); \] \[ \delta_{11} =\delta_{11R} +\delta_{11M} +\delta_{11N} ; \] \[ \delta_{14R} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{44} +R_{51} \cdot R_{54} +R_{61} \cdot R_{64} +R_{71} \cdot R_{74} +R_{81} \cdot R_{84} +R_{91} \cdot R_{94} \cdot 0.5} \right); \] \[ \delta_{14M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {M_{11} \cdot M_{24} +4\cdot M_{21} \cdot M_{24} +M_{21} \cdot M_{34} +M_{31} \cdot M_{24} +4\cdot M_{31} \cdot M_{34} +M_{31} \cdot M_{44} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{14N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{121} \cdot N_{124} +N_{231} \cdot N_{234} +N_{341} \cdot N_{344} +N_{451} \cdot N_{454} +} \right.} \\ {\left. {N_{561} \cdot N_{564} +N_{671} \cdot N_{674} +N_{781} \cdot N_{784} +N_{891} \cdot N_{894} } \right);} \\ \end{array} } \] \[ \delta_{14} =\delta_{14R} +\delta_{14M} +\delta_{14N} ; \] \[ \delta_{15R} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{45} +R_{51} \cdot R_{55} +R_{61} \cdot R_{65} } \right); \quad \delta_{15M} =0; \] \[ \delta_{15N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{451} \cdot N_{455} +N_{561} \cdot N_{565} } \right); \quad \delta_{15} =\delta_{15R} +\delta_{15M} +\delta_{15N} ; \] \[ \delta_{16R} =2\cdot \frac{1}{D}\cdot \left( {R_{51} \cdot R_{56} +R_{61} \cdot R_{66} +R_{71} \cdot R_{76} } \right); \quad \delta_{16M} =0; \] \[ \delta_{16N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{561} \cdot N_{566} +N_{671} \cdot N_{676} } \right); \quad \delta_{16} =\delta_{16R} +\delta_{16M} +\delta_{16N} ; \] \[ \delta_{17R} =2\cdot \frac{1}{D}\cdot \left( {R_{61} \cdot R_{67} +R_{71} \cdot R_{77} +R_{81} \cdot R_{87} } \right); \quad \delta_{17M} =0; \] \[ \delta_{17N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{671} \cdot N_{677} +N_{781} \cdot N_{787} } \right); \quad \delta_{17} =\delta_{17R} +\delta_{17M} +\delta_{17N} ; \] \[ \delta_{18R} =2\cdot \frac{1}{D}\cdot \left( {R_{71} \cdot R_{78} +R_{81} \cdot R_{88} +R_{91} \cdot R_{98} \cdot 0.5} \right); \quad \delta_{18M} =0; \] \[ \delta_{18N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{781} \cdot N_{788} +N_{891} \cdot N_{898} } \right); \quad \delta_{18} =\delta_{18R} +\delta_{18M} +\delta_{18N} ; \] \[ \delta_{19R} =2\cdot \frac{1}{D}\cdot \left( {R_{81} \cdot R_{89} +R_{91} \cdot R_{99} \cdot 0.5} \right); \quad \delta_{19M} =0; \quad \delta_{19N} =2\cdot \frac{S}{E\cdot F}\cdot N_{891} \cdot N_{899} ; \] \[ \delta_{19} =\delta_{19R} +\delta_{19M} +\delta_{19N} ; \] \[ \delta_{44R} =2\cdot \frac{1}{D}\cdot \left( {R_{44}^{2}+R_{54} ^{2}+R_{64}^{2}+R_{74}^{2}+R_{84}^{2}+R_{94}^{2}\cdot 0.5} \right); \] \[ \delta_{44M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot \left( {2\cdot M_{24} ^{2}+2\cdot M_{34}^{2}+M_{24} \cdot M_{34} +2\cdot M_{44}^{2}+M_{34} \cdot M_{44} } \right); \] \[ \delta_{44N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{124}^{2}+N_{234} ^{2}+N_{344}^{2}+N_{454}^{2}+N_{564}^{2}+N_{674}^{2}+N_{784} ^{2}+N_{894}^{2}} \right); \] \[ \delta_{44} =\delta_{44R} +\delta_{44M} +\delta_{44N} ; \] \[ \delta_{45R} =2\cdot \frac{1}{D}\cdot \left( {R_{44} \cdot R_{45} +R_{54} \cdot R_{55} +R_{64} \cdot R_{65} } \right); \quad \delta_{45M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{44} \cdot M_{55} ; \] \[ \delta_{45N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{454} \cdot N_{455} +N_{564} \cdot N_{565} } \right); \] \[ \delta_{45} =\delta_{45R} +\delta_{45M} +\delta_{45N} ; \] \[ \delta_{46R} =2\cdot \frac{1}{D}\cdot \left( {R_{54} \cdot R_{56} +R_{64} \cdot R_{66} +R_{74} \cdot R_{76} } \right); \quad \delta_{46M} =0; \quad \delta_{46N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{564} \cdot N_{566} +N_{674} \cdot N_{676} } \right); \] \[ \delta_{46} =\delta_{46R} +\delta_{46M} +\delta_{46N} ; \] \[ \delta_{47R} =2\cdot \frac{1}{D}\cdot \left( {R_{64} \cdot R_{67} +R_{74} \cdot R_{77} +R_{84} \cdot R_{87} } \right); \quad \delta_{47M} =0; \quad \delta_{47N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{674} \cdot N_{677} +N_{784} \cdot N_{787} } \right); \] \[ \delta_{47} =\delta_{47R} +\delta_{47M} +\delta_{47N} ; \] \[ \delta_{48R} =2\cdot \frac{1}{D}\cdot \left( {R_{74} \cdot R_{78} +R_{84} \cdot R_{88} +R_{94} \cdot R_{98} \cdot 0.5} \right); \quad \delta_{48M} =0; \quad \delta_{48N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{784} \cdot N_{788} +N_{894} \cdot N_{898} } \right); \] \[ \delta_{48} =\delta_{48R} +\delta_{48M} +\delta_{48N} ; \] \[ \delta_{49R} =2\cdot \frac{1}{D}\cdot \left( {R_{84} \cdot R_{89} +R_{94} \cdot R_{99} \cdot 0.5} \right); \quad \delta_{49M} =0; \quad \delta_{49N} =2\cdot \frac{S}{E\cdot F}\cdot N_{894} \cdot N_{899} ; \] \[ \delta_{49} =\delta_{49R} +\delta_{49M} +\delta_{49N} ; \] \[ \delta_{55R} =2\cdot \frac{1}{D}\cdot \left( {R_{45}^{2}+R_{55} ^{2}+R_{65}^{2}} \right); \quad \delta_{55M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{55}^{2}; \quad \delta_{55N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{455}^{2}+N_{565} ^{2}} \right); \] \[ \delta_{55} =\delta_{55R} +\delta_{55M} +\delta_{55N} ; \] \[ \delta_{56R} =2\cdot \frac{1}{D}\cdot \left( {R_{55} \cdot R_{56} +R_{65} \cdot R_{66} } \right); \quad \delta_{56M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{55} \cdot M_{66} ; \quad \delta_{56N} =2\cdot \frac{S}{E\cdot F}\cdot N_{565} \cdot N_{566} ; \] \[ \delta_{56} =\delta_{56R} +\delta_{56M} +\delta_{56N} ; \] \[ \delta_{57R} =2\cdot \frac{1}{D}\cdot R_{65} \cdot R_{67} ; \quad \delta_{57M} =0; \quad \delta_{57N} =0; \] \[ \delta_{57} =\delta_{57R} +\delta_{57M} +\delta_{57N} ; \] \[ \delta_{58R} =0; \quad \delta_{58M} =0; \quad \delta_{58N} =0; \] \[ \delta_{58} =\delta_{58R} +\delta_{58M} +\delta_{58N} ; \] \[ \delta_{59R} =0; \quad \delta_{59M} =0; \quad \delta_{59N} =0; \] \[ \delta_{59} =\delta_{59R} +\delta_{59M} +\delta_{59N} ; \] \[ \delta_{66R} =2\cdot \frac{1}{D}\cdot \left( {R_{56}^{2}+R_{66} ^{2}+R_{76}^{2}} \right); \quad \delta_{66M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{66}^{2}; \quad \delta_{66N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{566}^{2}+N_{676} ^{2}} \right); \] \[ \delta_{66} =\delta_{66R} +\delta_{66M} +\delta_{66N} ; \] \[ \delta_{67R} =2\cdot \frac{1}{D}\cdot \left( {R_{66} \cdot R_{67} +R_{76} \cdot R_{77} } \right); \quad \delta_{67M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{66} \cdot M_{77} ; \quad \delta_{67N} =2\cdot \frac{S}{E\cdot F}\cdot N_{676} \cdot N_{677} ; \] \[ \delta_{67} =\delta_{67R} +\delta_{67M} +\delta_{67N} ; \] \[ \delta_{68R} =2\cdot \frac{1}{D}\cdot R_{76} \cdot R_{78} ; \quad \delta_{68M} =0; \quad \delta_{68N} =0; \] \[ \delta_{68} =\delta_{68R} +\delta_{68M} +\delta_{68N} ; \] \[ \delta_{69R} =0; \quad \delta_{69M} =0; \quad \delta_{69N} =0; \] \[ \delta_{69} =\delta_{69R} +\delta_{69M} +\delta_{69N} ; \] \[ \delta_{77R} =2\cdot \frac{1}{D}\cdot \left( {R_{67}^{2}+R_{77} ^{2}+R_{87}^{2}} \right); \quad \delta_{77M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{77}^{2}; \quad \delta_{77N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{677}^{2}+N_{787} ^{2}} \right); \] \[ \delta_{77} =\delta_{77R} +\delta_{77M} +\delta_{77N} ; \] \[ \delta_{78R} =2\cdot \frac{1}{D}\cdot \left( {R_{77} \cdot R_{78} +R_{87} \cdot R_{88} } \right); \quad \delta_{78M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{77} \cdot M_{88} ; \quad \delta_{78N} =2\cdot \frac{S}{E\cdot F}\cdot N_{787} \cdot N_{788} ; \] \[ \delta_{78} =\delta_{78R} +\delta_{78M} +\delta_{78N} ; \] \[ \delta_{79R} =2\cdot \frac{1}{D}\cdot R_{87} \cdot R_{89} ; \quad \delta_{79M} =0; \quad \delta_{79N} =0; \] \[ \delta_{79} =\delta_{79R} +\delta_{79M} +\delta_{79N} ; \] \[ \delta_{88R} =2\cdot \frac{1}{D}\cdot \left( {R_{78}^{2}+R_{88} ^{2}+R_{98}^{2}\cdot 0.5} \right); \quad \delta_{88M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{88}^{2}; \quad \delta_{88N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{788}^{2}+N_{898} ^{2}} \right); \] \[ \delta_{88} =\delta_{88R} +\delta_{88M} +\delta_{88N} ; \] \[ \delta_{89R} =2\cdot \frac{1}{D}\cdot \left( {R_{88} \cdot R_{89} +R_{98} \cdot R_{99} \cdot 0.5} \right); \quad \delta_{89M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{88} \cdot M_{99} ; \quad \delta_{89N} =2\cdot \frac{S}{E\cdot F}\cdot N_{898} \cdot N_{899} ; \] \[ \delta_{89} =\delta_{89R} +\delta_{89M} +\delta_{89N} ; \] \[ \delta_{99R} =2\cdot \frac{1}{D}\cdot \left( {R_{89}^{2}+R_{99}^{2}\cdot 0.5} \right); \quad \delta_{99M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot M_{99}^{2}; \quad \delta_{99N} =2\cdot \frac{S}{E\cdot F}\cdot N_{899}^{2}; \] \[ \delta_{99} =\delta_{99R} +\delta_{99M} +\delta_{99N} ; \] \[ \delta_{1pR} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{4p} +R_{51} \cdot R_{5p} +R_{61} \cdot R_{6p} +R_{71} \cdot R_{7p} +R_{81} \cdot R_{8p} +R_{91} \cdot R_{9p} \cdot 0.5} \right); \] \[ \delta_{1pM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{2p} \cdot M_{21} +M_{2p} \cdot M_{11} +4\cdot M_{3p} \cdot M_{31} +M_{3p} \cdot M_{21} +M_{2p} \cdot M_{31} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{1pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12p} \cdot N_{121} +N_{23p} \cdot N_{231} +N_{34p} \cdot N_{341} +N_{45p} \cdot N_{451} +} \right.} \\ {\left. {N_{56p} \cdot N_{561} +N_{67p} \cdot N_{671} +N_{78p} \cdot N_{781} +N_{89p} \cdot N_{891} } \right);} \\ \end{array} } \] \[ \delta_{1p} =\delta_{1pR} +\delta_{1pM} +\delta_{1pN} ; \] \[ \delta_{4pR} =2\cdot \frac{1}{D}\cdot \left( {R_{44} \cdot R_{4p} +R_{54} \cdot R_{5p} +R_{64} \cdot R_{6p} +R_{74} \cdot R_{7p} +R_{84} \cdot R_{8p} +R_{94} \cdot R_{9p} \cdot 0.5} \right); \] \[ \delta_{4pM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{2p} \cdot M_{24} +4\cdot M_{3p} \cdot M_{34} +M_{3p} \cdot M_{24} +M_{2p} \cdot M_{34} +M_{3p} \cdot M_{44} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{4pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12p} \cdot N_{124} +N_{23p} \cdot N_{234} +N_{34p} \cdot N_{344} +N_{45p} \cdot N_{454} +} \right.} \\ {\left. {N_{56p} \cdot N_{564} +N_{67p} \cdot N_{674} +N_{78p} \cdot N_{784} +N_{89p} \cdot N_{894} } \right);} \\ \end{array} } \] \[ \delta_{4p} =\delta_{4pR} +\delta_{4pM} +\delta_{4pN} ; \] \[ \delta_{5pR} =2\cdot \frac{1}{D}\cdot \left( {R_{45} \cdot R_{4p} +R_{55} \cdot R_{5p} +R_{65} \cdot R_{6p} } \right); \quad \delta_{5pM} =0; \quad \delta_{5pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{45p} \cdot N_{455} +N_{56p} \cdot N_{565} } \right); \] \[ \delta_{5p} =\delta_{5pR} +\delta_{5pM} +\delta_{5pN} ; \] \[ \delta_{6pR} =2\cdot \frac{1}{D}\cdot \left( {R_{56} \cdot R_{5p} +R_{66} \cdot R_{6p} +R_{76} \cdot R_{7p} } \right); \quad \delta_{6pM} =0; \quad \delta_{6pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{56p} \cdot N_{566} +N_{67p} \cdot N_{676} } \right); \] \[ \delta_{6p} =\delta_{6pR} +\delta_{6pM} +\delta_{6pN} ; \] \[ \delta_{7pR} =2\cdot \frac{1}{D}\cdot \left( {R_{67} \cdot R_{6p} +R_{77} \cdot R_{7p} +R_{87} \cdot R_{8p} } \right); \quad \delta_{7pM} =0; \quad \delta_{7pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{67p} \cdot N_{677} +N_{78p} \cdot N_{787} } \right); \] \[ \delta_{7p} =\delta_{7pR} +\delta_{7pM} +\delta_{7pN} ; \] \[ \delta_{8pR} =2\cdot \frac{1}{D}\cdot \left( {R_{78} \cdot R_{7p} +R_{88} \cdot R_{8p} +R_{98} \cdot R_{9p} \cdot 0.5} \right); \quad \delta_{8pM} =0; \quad \delta_{8pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{78p} \cdot N_{788} +N_{89p} \cdot N_{898} } \right); \] \[ \delta_{8p} =\delta_{8pR} +\delta_{8pM} +\delta_{8pN} ; \] \[ \delta_{9pR} =2\cdot \frac{1}{D}\cdot \left( {R_{89} \cdot R_{8p} +R_{99} \cdot R_{9p} \cdot 0.5} \right); \quad \delta_{9pM} =0; \quad \delta_{9pN} =2\cdot \frac{S}{E\cdot F}\cdot N_{89p} \cdot N_{899} ; \] \[ \delta_{9p} =\delta_{9pR} +\delta_{9pM} +\delta_{9pN} ; \] \[ \delta_{1qR} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{4q} +R_{51} \cdot R_{5q} +R_{61} \cdot R_{6q} +R_{71} \cdot R_{7q} +R_{81} \cdot R_{8q} +R_{91} \cdot R_{9q} \cdot 0.5} \right); \] \[ \delta_{1qM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{2q} \cdot M_{21} +M_{2q} \cdot M_{11} +4\cdot M_{3q} \cdot M_{31} +M_{3q} \cdot M_{21} +M_{2q} \cdot M_{31} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{1qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12q} \cdot N_{121} +N_{23q} \cdot N_{231} +N_{34q} \cdot N_{341} +N_{45q} \cdot N_{451} +} \right.} \\ {\left. {N_{56q} \cdot N_{561} +N_{67q} \cdot N_{671} +N_{78q} \cdot N_{781} +N_{89q} \cdot N_{891} } \right);} \\ \end{array} } \] \[ \delta_{1q} =\delta_{1qR} +\delta_{1qM} +\delta_{1qN} ; \] \[ \delta_{4qR} =2\cdot \frac{1}{D}\cdot \left( {R_{44} \cdot R_{4q} +R_{54} \cdot R_{5q} +R_{64} \cdot R_{6q} +R_{74} \cdot R_{7q} +R_{84} \cdot R_{8q} +R_{94} \cdot R_{9q} \cdot 0.5} \right); \] \[ \delta_{4qM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{qp} \cdot M_{24} +4\cdot M_{qp} \cdot M_{34} +M_{3q} \cdot M_{24} +M_{2q} \cdot M_{34} +M_{3q} \cdot M_{44} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{4qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12q} \cdot N_{124} +N_{23q} \cdot N_{234} +N_{34q} \cdot N_{344} +N_{45q} \cdot N_{454} +} \right.} \\ {\left. {N_{56q} \cdot N_{564} +N_{67q} \cdot N_{674} +N_{78q} \cdot N_{784} +N_{89q} \cdot N_{894} } \right);} \\ \end{array} } \] \[ \delta_{4q} =\delta_{4qR} +\delta_{4qM} +\delta_{4qN} ; \] \[ \delta_{5qR} =2\cdot \frac{1}{D}\cdot \left( {R_{45} \cdot R_{4q} +R_{55} \cdot R_{5q} +R_{65} \cdot R_{6q} } \right); \quad \delta_{5qM} =0; \quad \delta_{5qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{45q} \cdot N_{455} +N_{56q} \cdot N_{565} } \right); \] \[ \delta_{5q} =\delta_{5qR} +\delta_{5qM} +\delta_{5qN} ; \] \[ \delta_{6qR} =2\cdot \frac{1}{D}\cdot \left( {R_{56} \cdot R_{5q} +R_{66} \cdot R_{6q} +R_{76} \cdot R_{7q} } \right); \quad \delta_{6qM} =0; \quad \delta_{6qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{56q} \cdot N_{566} +N_{67q} \cdot N_{676} } \right); \] \[ \delta_{6q} =\delta_{6qR} +\delta_{6qM} +\delta_{6qN} ; \] \[ \delta_{7qR} =2\cdot \frac{1}{D}\cdot \left( {R_{67} \cdot R_{6q} +R_{77} \cdot R_{7q} +R_{87} \cdot R_{8q} } \right); \quad \delta_{7qM} =0; \quad \delta_{7qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{67q} \cdot N_{677} +N_{78q} \cdot N_{787} } \right); \] \[ \delta_{7q} =\delta_{7qR} +\delta_{7qM} +\delta_{7qN} ; \] \[ \delta_{8qR} =2\cdot \frac{1}{D}\cdot \left( {R_{78} \cdot R_{7q} +R_{88} \cdot R_{8q} +R_{98} \cdot R_{9q} \cdot 0.5} \right); \quad \delta_{8qM} =0; \quad \delta_{8qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{78q} \cdot N_{788} +N_{89q} \cdot N_{898} } \right); \] \[ \delta_{8q} =\delta_{8qR} +\delta_{8qM} +\delta_{8qN} ; \] \[ \delta_{9qR} =2\cdot \frac{1}{D}\cdot \left( {R_{89} \cdot R_{8q} +R_{99} \cdot R_{9q} \cdot 0.5} \right); \quad \delta_{9qM} =0; \quad \delta_{9qN} =2\cdot \frac{S}{E\cdot F}\cdot N_{89q} \cdot N_{899} ; \] \[ \delta_{9q} =\delta_{9qR} +\delta_{9qM} +\delta_{9qN} . \]

Determination of redundants

\[ \Delta_{1} =\left[ {{\begin{array}{*{20}c} {\delta_{11} } & {\delta_{14} } & {\delta_{15} } & {\delta_{16} } & {\delta_{17} } & {\delta_{18} } & {\delta_{19} } \\ {\delta_{14} } & {\delta_{44} } & {\delta_{45} } & {\delta_{46} } & {\delta_{47} } & {\delta_{48} } & {\delta_{49} } \\ {\delta_{15} } & {\delta_{45} } & {\delta_{55} } & {\delta_{56} } & {\delta_{57} } & {\delta_{58} } & {\delta_{59} } \\ {\delta_{16} } & {\delta_{46} } & {\delta_{56} } & {\delta_{66} } & {\delta_{67} } & {\delta_{68} } & {\delta_{69} } \\ {\delta_{17} } & {\delta_{47} } & {\delta_{57} } & {\delta_{67} } & {\delta_{77} } & {\delta_{78} } & {\delta_{79} } \\ {\delta_{18} } & {\delta_{48} } & {\delta_{58} } & {\delta_{68} } & {\delta_{78} } & {\delta_{88} } & {\delta_{89} } \\ {\delta_{19} } & {\delta_{49} } & {\delta_{59} } & {\delta_{69} } & {\delta_{79} } & {\delta_{89} } & {\delta_{99} } \\ \end{array} }} \right] \quad \Delta_{pq} =\left[ {{\begin{array}{*{20}c} {\delta_{1p} +\delta_{1q} } \\ {\delta_{4p} +\delta_{4q} } \\ {\delta_{5p} +\delta_{5q} } \\ {\delta_{6p} +\delta_{6q} } \\ {\delta_{7p} +\delta_{7q} } \\ {\delta_{8p} +\delta_{8q} } \\ {\delta_{9p} +\delta_{9q} } \\ \end{array} }} \right] \quad X=-\Delta_{1}^{-1}\cdot \Delta_{pq} =\left[ {{\begin{array}{*{20}c} {X_{1} } \\ {X_{4} } \\ {X_{5} } \\ {X_{6} } \\ {X_{7} } \\ {X_{8} } \\ {X_{9} } \\ \end{array} }} \right] \]

Determination of internal forces

\[ M_{1} =M_{11} \cdot X_{1} ; \quad N_{12} =N_{121} \cdot X_{1} +N_{124} \cdot X_{4} +N_{12p} +N_{12q} ; \] \[ M_{2} =M_{21} \cdot X_{1} +M_{24} \cdot X_{4} +M_{2p} +M_{2q} ; \quad N_{23} =N_{231} \cdot X_{1} +N_{234} \cdot X_{4} +N_{23p} +N_{23q} ; \] \[ M_{3} =M_{31} \cdot X_{1} +M_{34} \cdot X_{4} +M_{3p} +M_{3q} ; \quad N_{34} =N_{341} \cdot X_{1} +N_{344} \cdot X_{4} +N_{34p} +N_{34q} ; \] \[ M_{4} =M_{44} \cdot X_{4} ; \quad N_{45} =N_{451} \cdot X_{1} +N_{454} \cdot X_{4} +N_{455} \cdot X_{5} +N_{45p} +N_{45q} ; \] \[ M_{5} =M_{55} \cdot X_{5} ; \quad N_{56} =N_{561} \cdot X_{1} +N_{564} \cdot X_{4} +N_{565} \cdot X_{5} +N_{566} \cdot X_{6} +N_{56p} +N_{56q} ; \] \[ M_{6} =M_{66} \cdot X_{6} ; \quad N_{67} =N_{671} \cdot X_{1} +N_{674} \cdot X_{4} +N_{676} \cdot X_{6} +N_{677} \cdot X_{7} +N_{67p} +N_{67q} ; \] \[ M_{7} =M_{77} \cdot X_{7} ; \quad N_{78} =N_{781} \cdot X_{1} +N_{784} \cdot X_{4} +N_{787} \cdot X_{7} +N_{788} \cdot X_{8} +N_{78p} +N_{78q} ; \] \[ M_{8} =M_{88} \cdot X_{8} ; \quad N_{89} =N_{891} \cdot X_{1} +N_{894} \cdot X_{4} +N_{898} \cdot X_{8} +N_{899} \cdot X_{9} +N_{89p} +N_{89q} ; \] \[ M_{9} =M_{99} \cdot X_{9} . \]

Determination of elastic reactions