Flexible Ring Subjected to Two Mutually Balanced Radially Compressive Forces
Objective: Determination of maximum displacements and bending moments in a flexible ring subjected to two mutually balanced radially compressive forces in the geometrically nonlinear formulation.
Initial data files:
| File name | Description |
|---|---|
| Кольцо_Q_50.spr | The flexible ring is subjected to the radially compressive forces Q = 50 kN |
Problem formulation: The flexible ring of constant cross-section is subjected to two mutually balanced radially compressive forces Q. Determine: the transverse displacements w and the bending moments M in the compressive force application points.
References: E. P. Popov, Theory and Calculation of Flexible Elastic Bars, Moscow, Nauka, 1986, p. 154
Initial data:
| EF = 1.5·107 kN | - axial stiffness of the cross-section of the ring; |
| EIy = 3.125·105 kN∙m2 | - bending stiffness of the cross-section of the ring in its plane; |
| EIz = 1.250·106 kN∙m2 | - bending stiffness of the cross-section of the ring out of its plane; |
| GIx = 3.533·105 kN∙m2 | - torsional stiffness of the cross-section of the ring; |
| R = 50.0 m | - radius of the ring; |
| Q = 50 kN | - value of the compressive forces. |
Finite element model: Design model – general type system. Elements of the plate - 180 bar elements taking into account the geometric nonlinearity of type 310. The spacing of the finite element mesh along the longitudinal axis of the ring is 2.0º. The dimensional stability of the design model is provided by imposing constraints according to its symmetry conditions. The nonlinear loading was generated for the incremental-iterative method with a loading factor - 1, number of steps - 1, number of iterations - 7 for the linear loading Q. Number of nodes in the design model – 180.
Results in SCAD
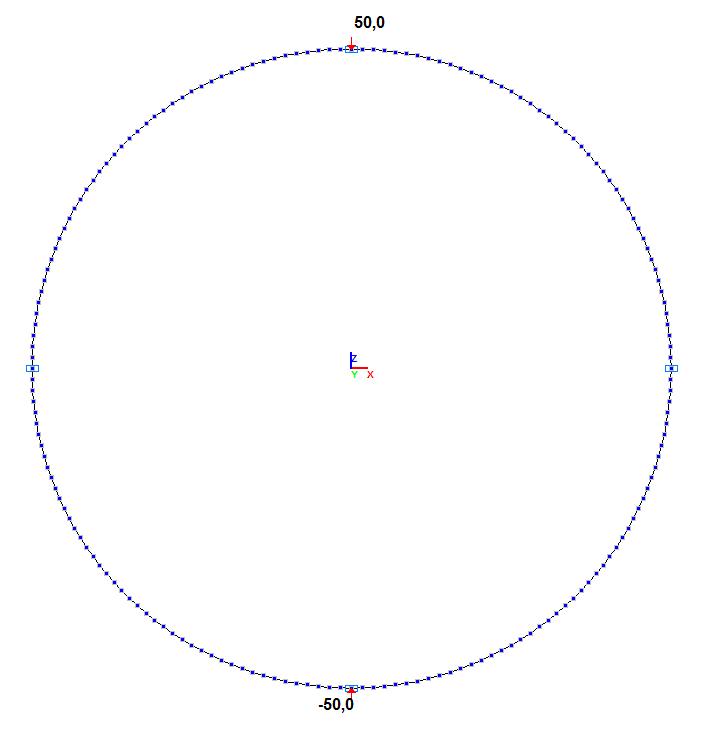
Design model
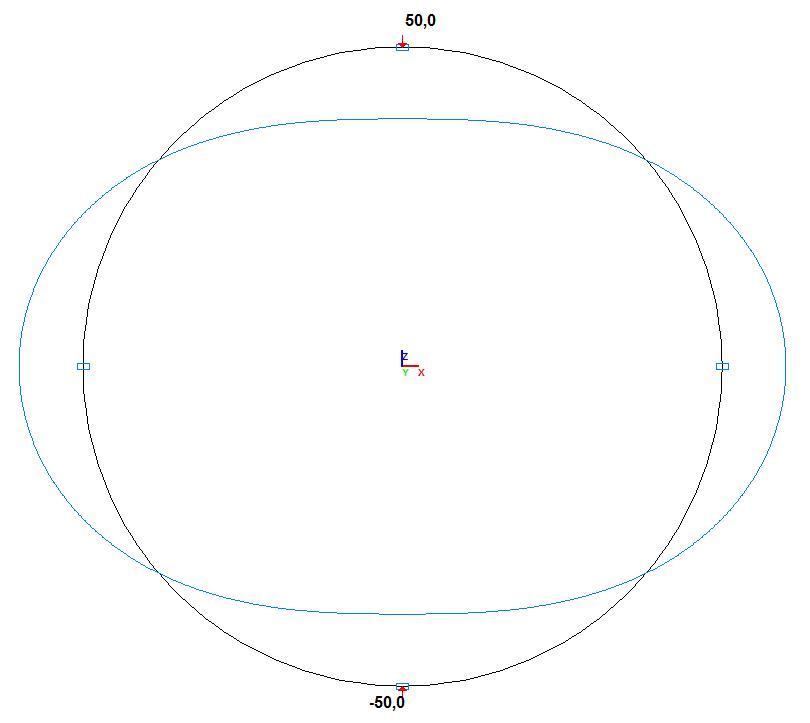
Deformed model
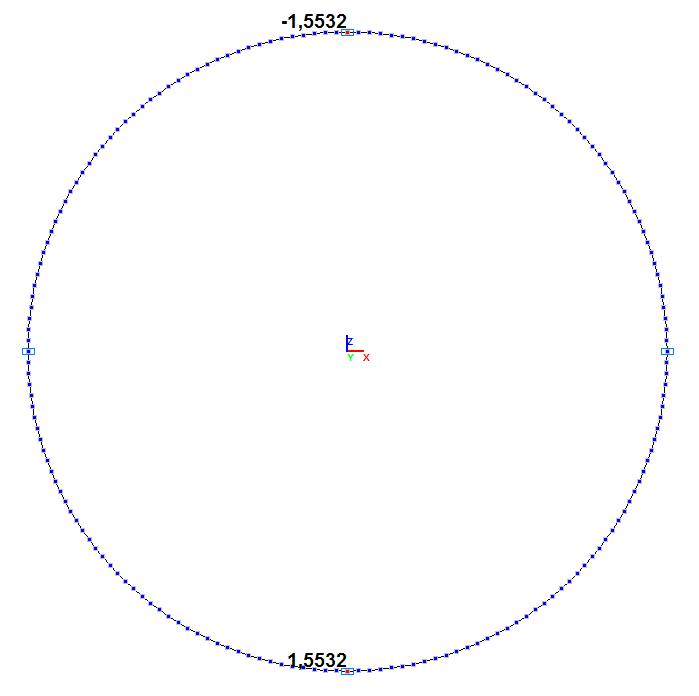
Values of transverse displacements w (m)
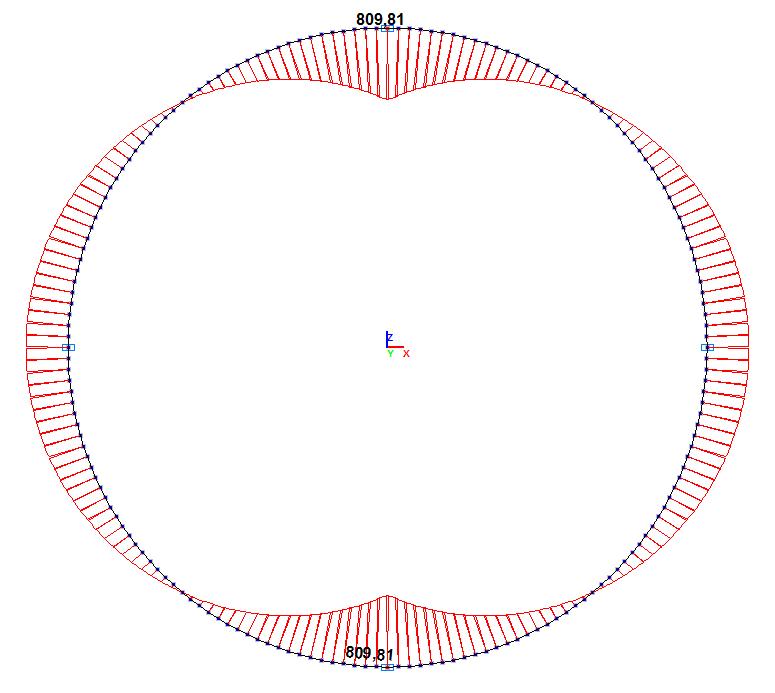
Bending moment diagrams M (kN∙m)
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviation, % |
|---|---|---|---|
|
The transverse displacement of the ring section w, m in the points of the application of the compressive forces Q = 50 kN |
±1.6060 |
±1.5532 |
3.29 |
|
The bending moment for the ring section M, kN∙m in the points of the application of the compressive forces Q = 50 kN |
809.37 |
809.81 |
0.05 |
Notes: In the analytical solution the transverse displacements w and the bending moments M in the compressive force application points can be determined according to the following formulas:
At \( \quad 0\le Q\le 0.6297\cdot \frac{EI}{R^{2}}: \) \[ w=\left[ {\frac{2}{k}\cdot \sqrt {\frac{2\cdot EI}{Q\cdot R^{2}}} \cdot E\left( {\frac{\pi }{4}} \right)-\left( {\frac{2}{k^{2}}-1} \right)\cdot \frac{\pi }{2}} \right]\cdot R; \quad M=\frac{2}{k}\cdot \sqrt {1-\frac{k^{2}}{2}} \cdot \sqrt {\frac{Q\cdot EI}{2}} -\frac{EI}{R}, \]
where \( k \) is determined by solving the equation: \(k\cdot F\left( {\frac{\pi }{4}} \right)=\frac{\pi \cdot R}{2}\cdot \sqrt {\frac{Q}{2\cdot EI}} ;\)
\( F\left( {\frac{\pi }{4}} \right)=\int\limits_0^{\frac{\pi }{4}} {\frac{d\phi }{\sqrt {1-k^{2}\cdot \sin^{2}\left( \phi \right)} }} \) Legendre elliptic integral of the first kind,
\( E\left( {\frac{\pi }{4}} \right)=\int\limits_0^{\frac{\pi }{4}} {\sqrt {1-k^{2}\cdot \sin^{2}\left( \phi \right)} \cdot d\phi } \) Legendre elliptic integral of the second kind.
At \(0.6297\cdot \frac{EI}{R^{2}}\le Q\le 2.7865\cdot \frac{EI}{R^{2}}: \)
\[ w=\left[ {2\cdot \sqrt {\frac{2\cdot EI}{Q\cdot R^{2}}} \cdot E\left( \Psi \right)-\frac{\pi }{2}} \right]\cdot R; \quad M=2\cdot k\cdot \cos \left( \Psi \right)\cdot \sqrt {\frac{Q\cdot EI}{2}} -\frac{EI}{R}, \]
where \( k \) and \( \Psi \) are determined by solving the system of equations: \( \left\{ {{\begin{array}{*{20}c} {k\cdot \sin \left( \Psi \right)=\frac{\sqrt 2 }{2}} \\ {F\left( \Psi \right)=\frac{\pi \cdot R}{2}\cdot \sqrt {\frac{Q}{2\cdot EI}} } \\ \end{array} }} \right.; \)
\( F\left( \Psi \right)=\int\limits_0^\Psi {\frac{d\psi }{\sqrt {1-k^{2}\cdot \sin^{2}\left( \psi \right)} }} \) Legendre elliptic integral of the first kind,
\( E\left( \Psi \right)=\int\limits_0^\Psi {\sqrt {1-k^{2}\cdot \sin^{2}\left( \psi \right)} \cdot d\psi } \) Legendre elliptic integral of the second kind.
