Rectangular Plate with Constant Curvature

Objective: Check of the obtained values of the stresses on the external surface for a rectangular plate at an irregular coarse finite element mesh.

Initial data files:

File name	Description
Patch_test_Constant_curvature_Shell_42.spr	Design model with the elements of type 42
Patch_test_Constant_curvature_Shell_44.spr	Design model with the elements of type 44
Patch_test_Constant_curvature_Shell_45.spr	Design model with the elements of type 45
Patch_test_Constant_curvature_Shell_50.spr	Design model with the elements of type 50

 

Problem formulation: The rectangular isotropic plate of constant thickness is subjected to the displacements and rotations of the outer edges providing the constant curvature (stresses on the external surface). Check that the constant curvature κ_x, κ_y, κ_xy (stresses on the external surface σ_x, σ_y, τ_xy) is provided.

References: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.

J. Robinson, S. Blackham, An evaluation of plate bending elements: MSC/NASTRAN, ASAS, PARFEC, ANSYS and SAP4, Dorset, Robinson and associates, 1981.

Initial data:

E = 1.0·106 kPa	- elastic modulus of the plate material;
ν = 0.25	- Poisson’s ratio;
t = 0.001 m	- thickness of the plate;
a = 0.12 m	- short side of the plate;
b = 0.24 m	- long side of the plate;

Boundary conditions:

w = 10-3∙(x2 + x∙y + y2)/2	- displacement of the outer edges along the normal to the surface of the plate;
θx = 10-3∙(x/2 + y)	- rotation of the outer edges about the short sides of the plate;
θy = 10-3∙( – x – y/2)	- rotation of the outer edges about the long sides of the plate.

 

Location of internal nodes of the finite element mesh:

Numbers of nodes in the Figure 1	x	y
1	0.04	0.02
2	0.18	0.03
3	0.16	0.08
4	0.08	0.08

 

Finite element model: Design model – general type system. Four design models are considered:

Model 1 - 10 three-node shell elements of type 42. Boundary conditions are provided by imposing constraints on the nodes of the outer edges of the plate in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ and their displacement (rotation) in accordance with the specified values w,  θ_x and θ_y. Number of nodes in the model – 8.

Model 2 - 5 four-node shell elements of type 44. Boundary conditions are provided by imposing constraints on the nodes of the outer edges of the plate in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ and their displacement (rotation) in accordance with the specified values w,  θ_x and θ_y. Number of nodes in the model – 8.

Model 3 – 10 six-node shell elements of type 45. Boundary conditions are provided by imposing constraints on the nodes of the outer edges of the plate in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ and their displacement (rotation) in accordance with the specified values w,  θ_x and θ_y. Number of nodes in the model – 25.

Model 4 - 5 eight-node shell elements of type 50. Boundary conditions are provided by imposing constraints on the nodes of the outer edges of the plate in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ and their displacement (rotation) in accordance with the specified values w,  θ_x and θ_y. Number of nodes in the model – 20.

 

Results in SCAD

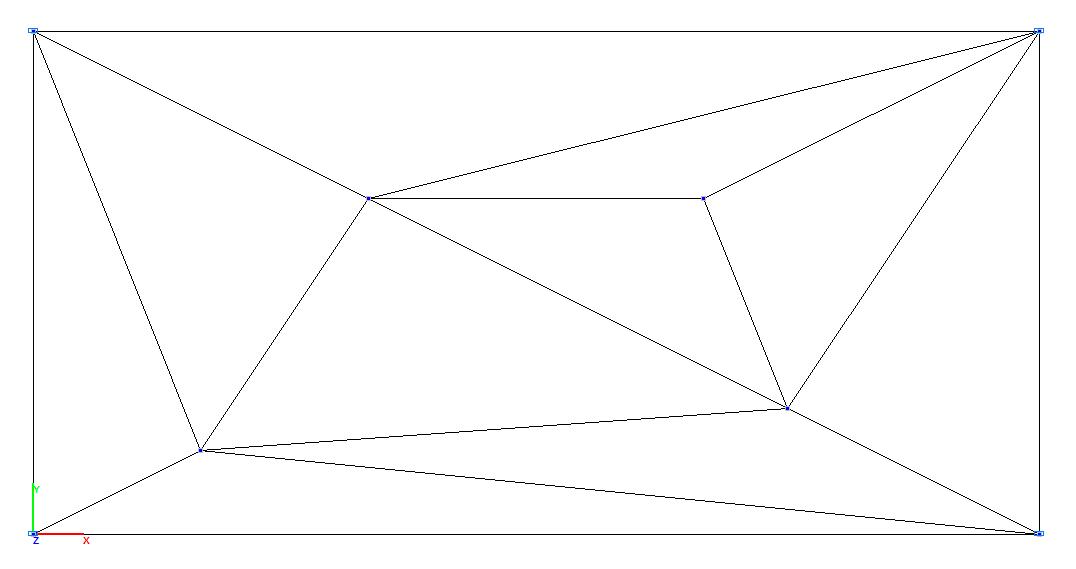
Model 1. Design model

 

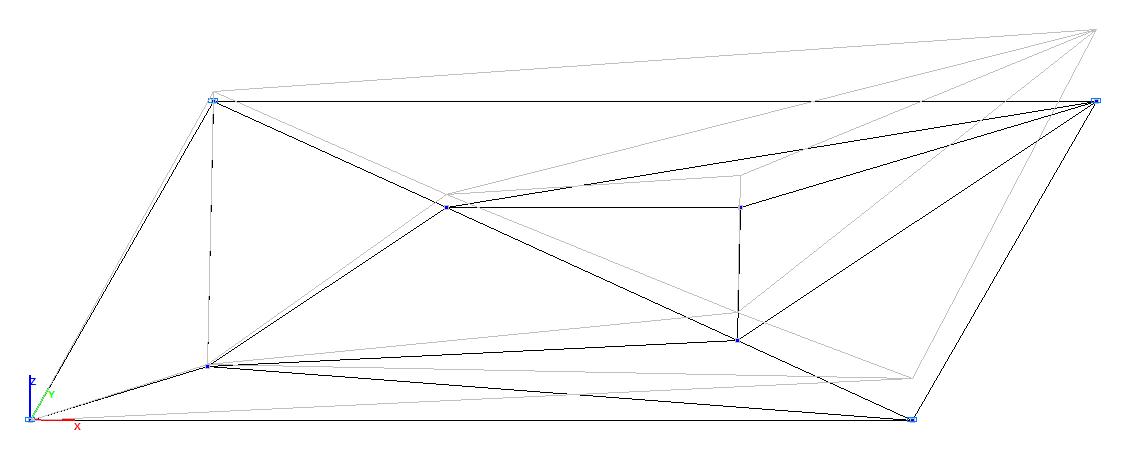
Model 1. Deformed model

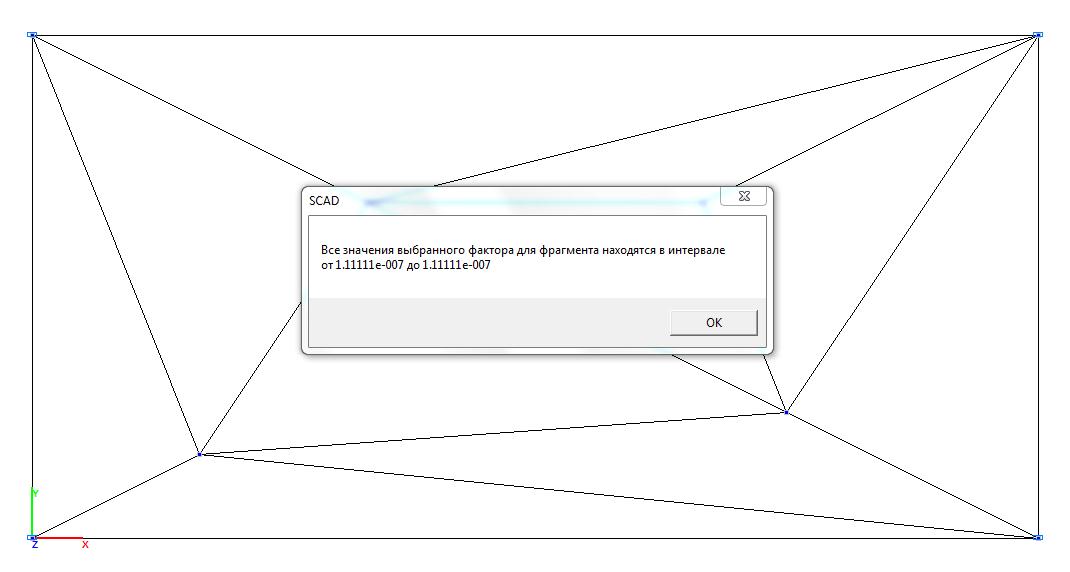
Model 1. Values of the bending moment M_x (kN∙m/m)

 

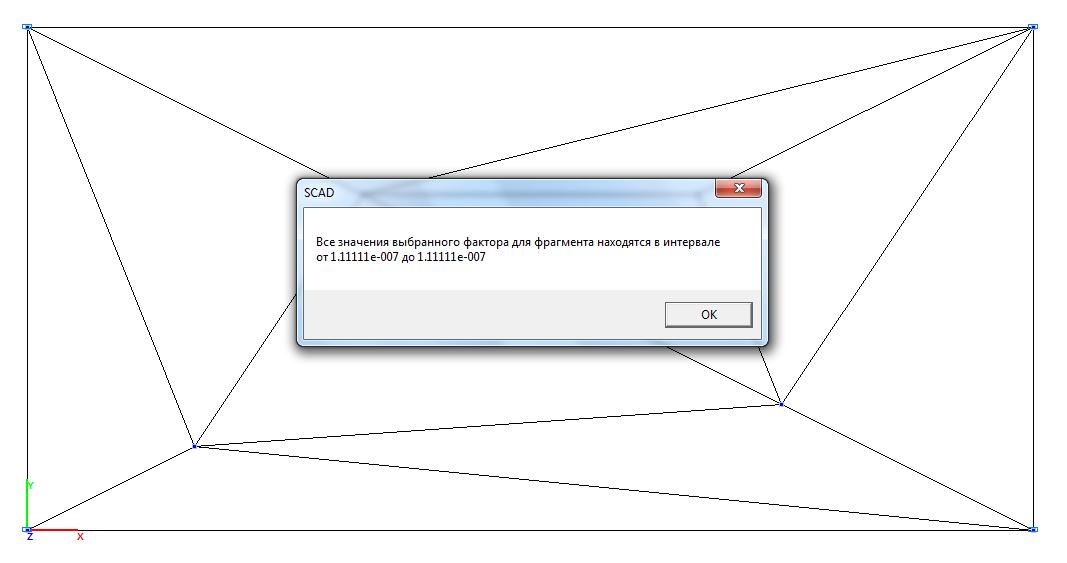
Model 1. Values of the bending moment M_y (kN∙m/m)

 

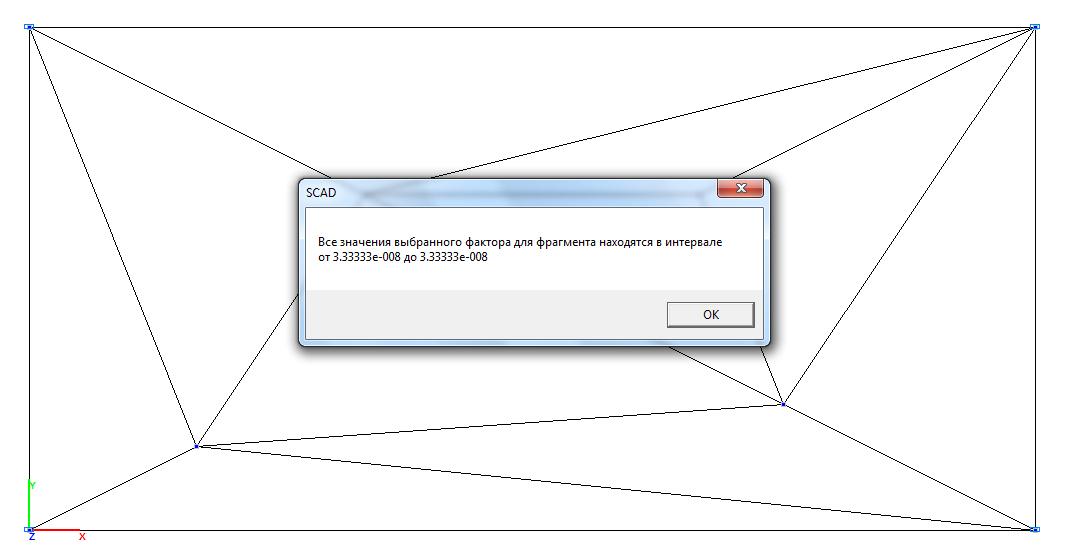
Model 1. Values of the torque M_xy (kN∙m/m)

 

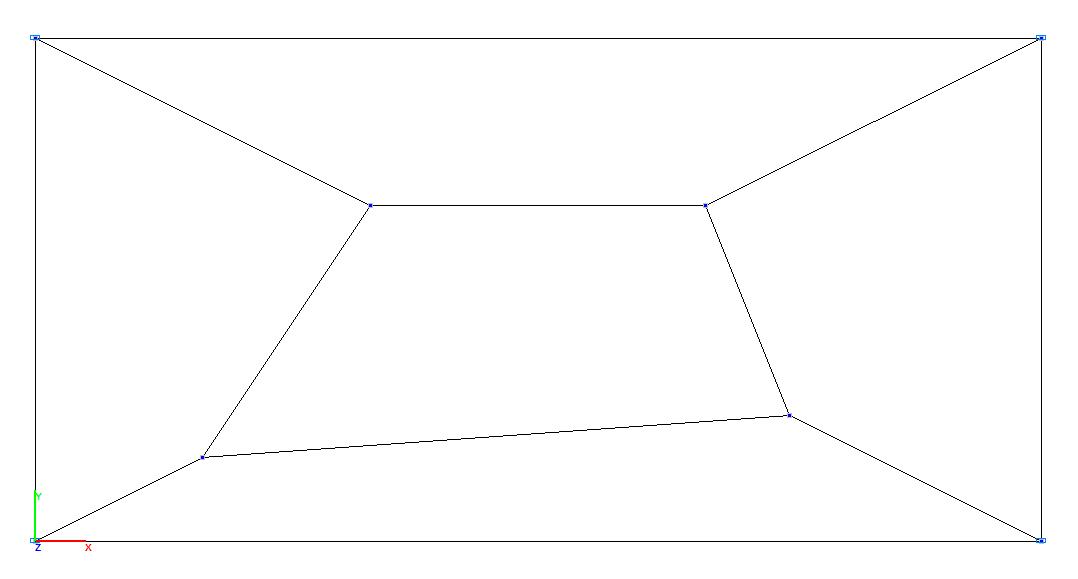
Model 2. Design model

 

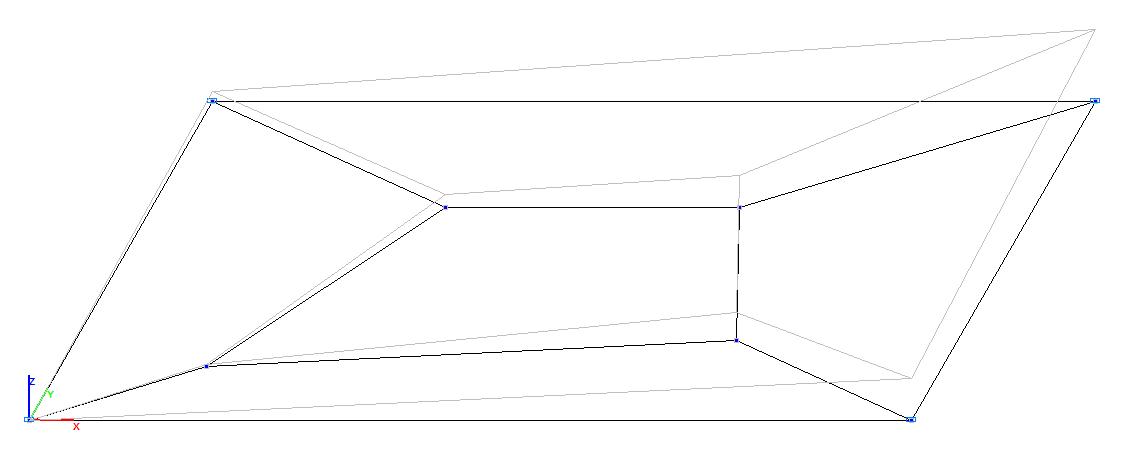
Model 2. Deformed model

 

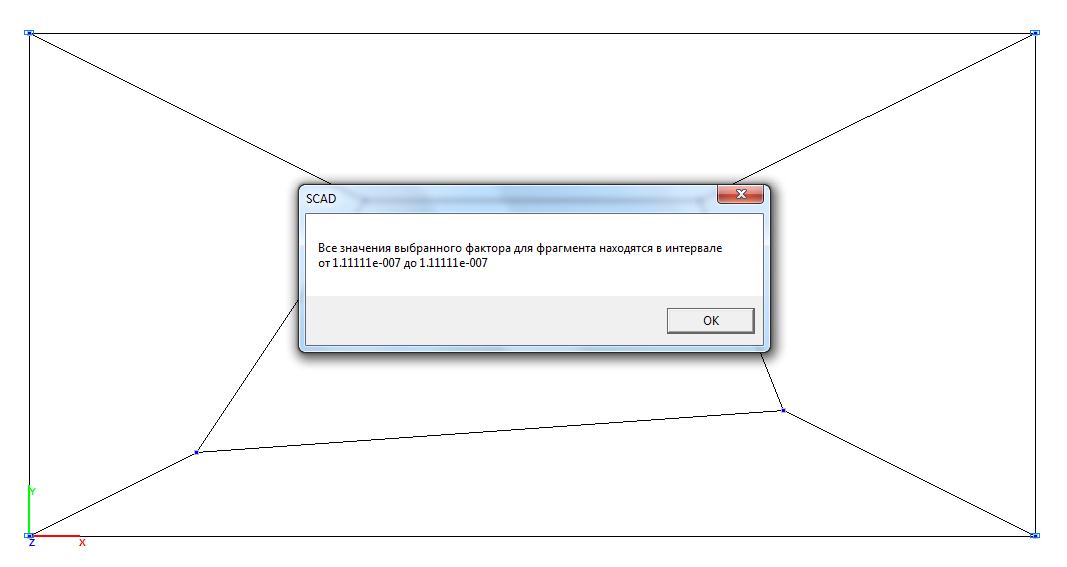
Model 2. Values of the bending moment M_x (kN∙m/m)

 

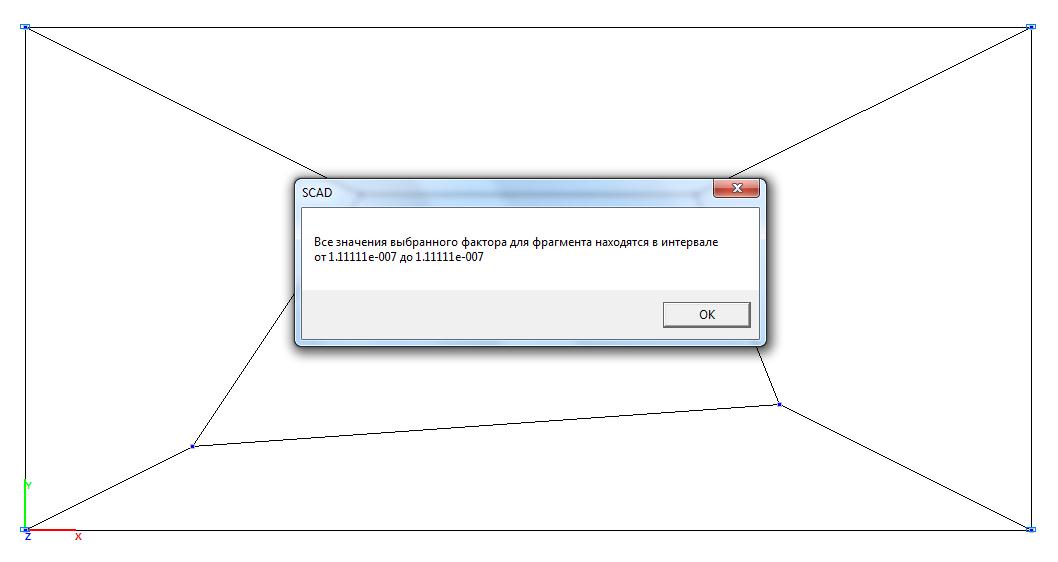
Model 2. Values of the bending moment M_y (kN∙m/m)

 

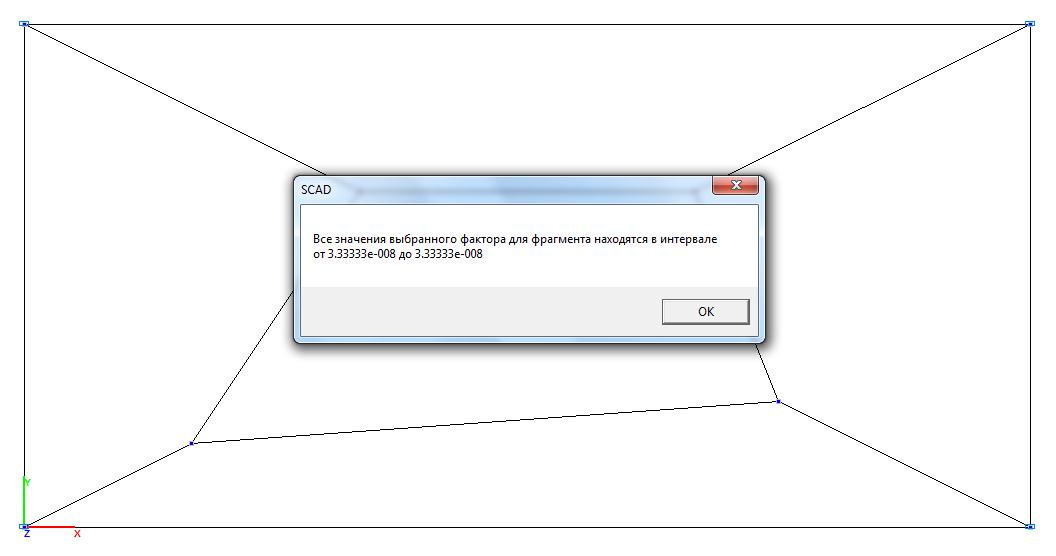
Model 2. Values of the torque M_xy (kN∙m/m)

 

Model 3. Design model

 

Model 3. Deformed model

 

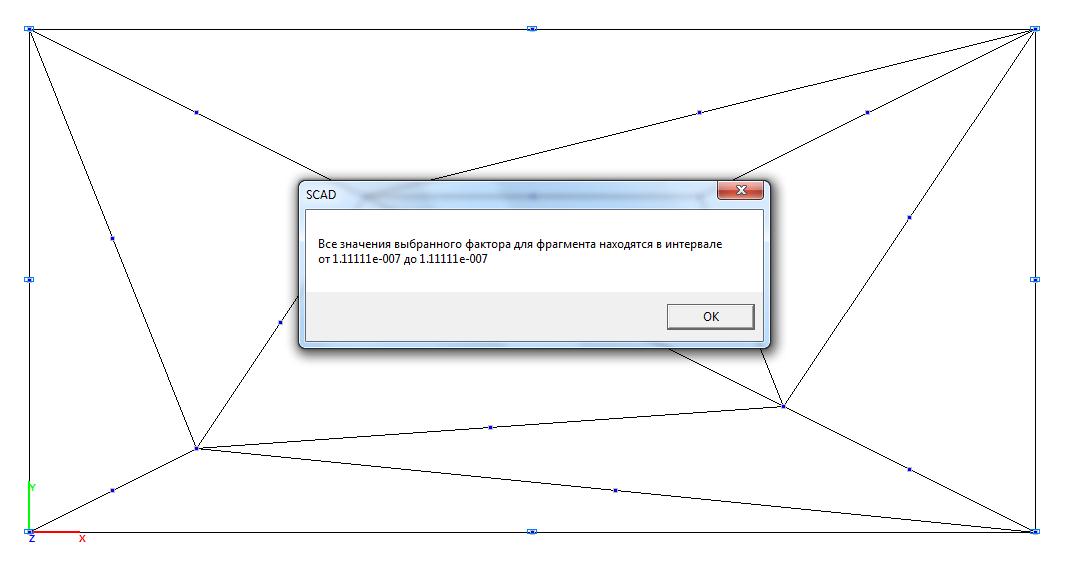
Model 3. Values of the bending moment M_x (kN∙m/m)

 

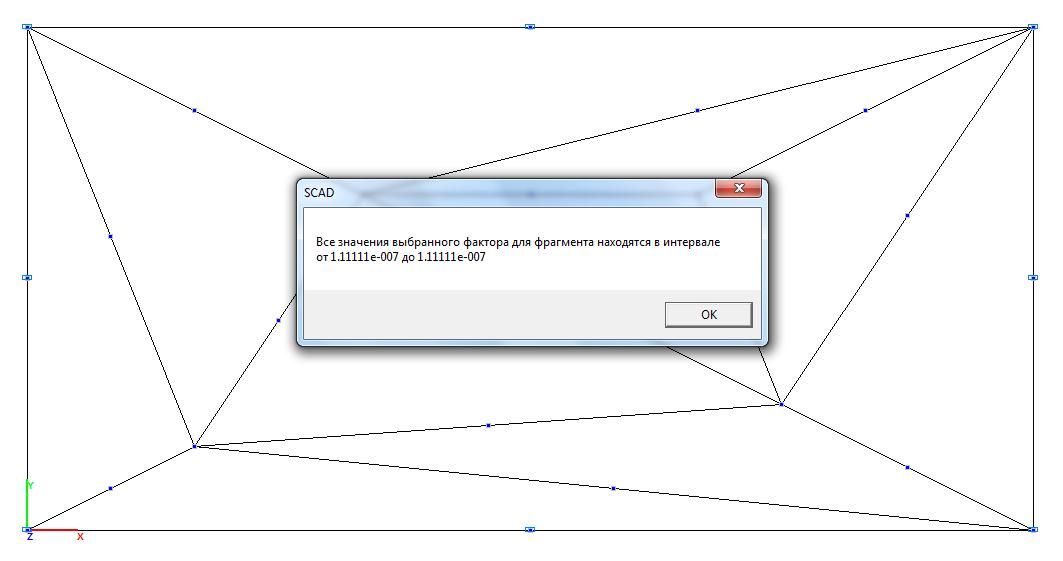
Model 3. Values of the bending moment M_y (kN∙m/m)

 

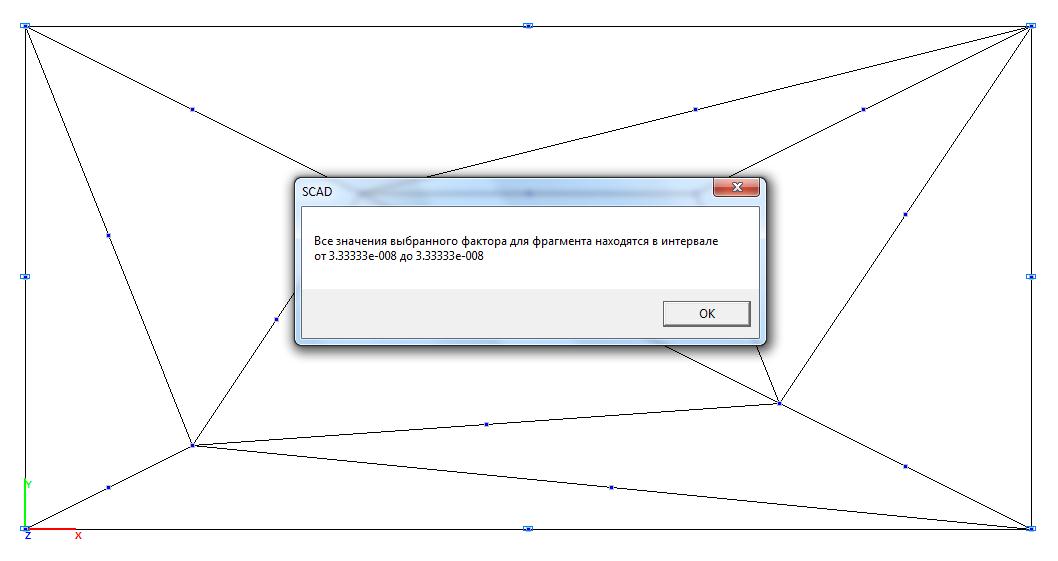
Model 3. Values of the torque M_xy (kN∙m/m)

 

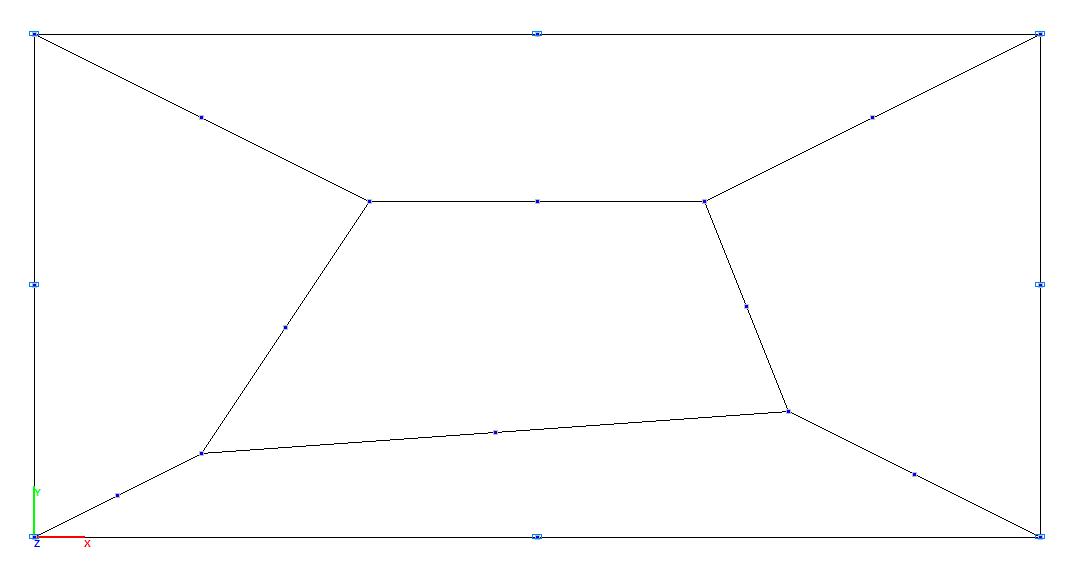
Model 4. Design model

 

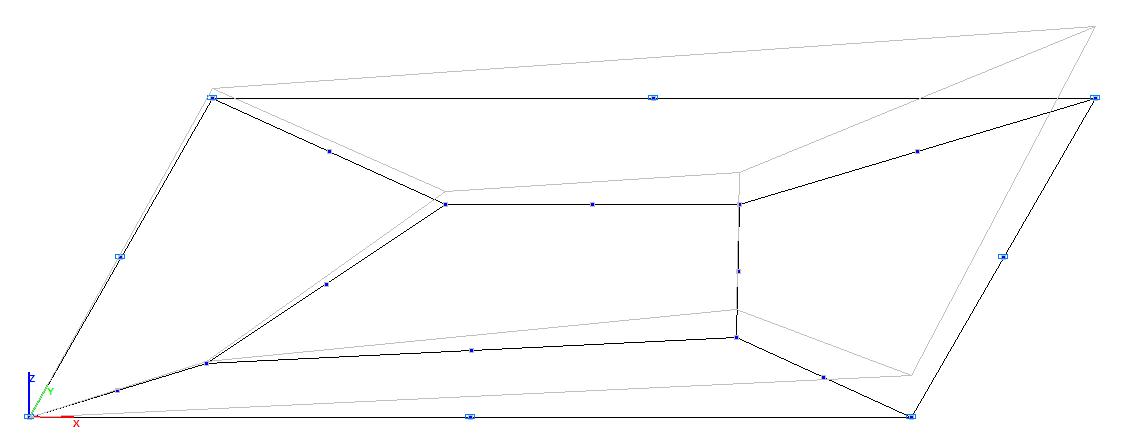
Model 4. Deformed model

 

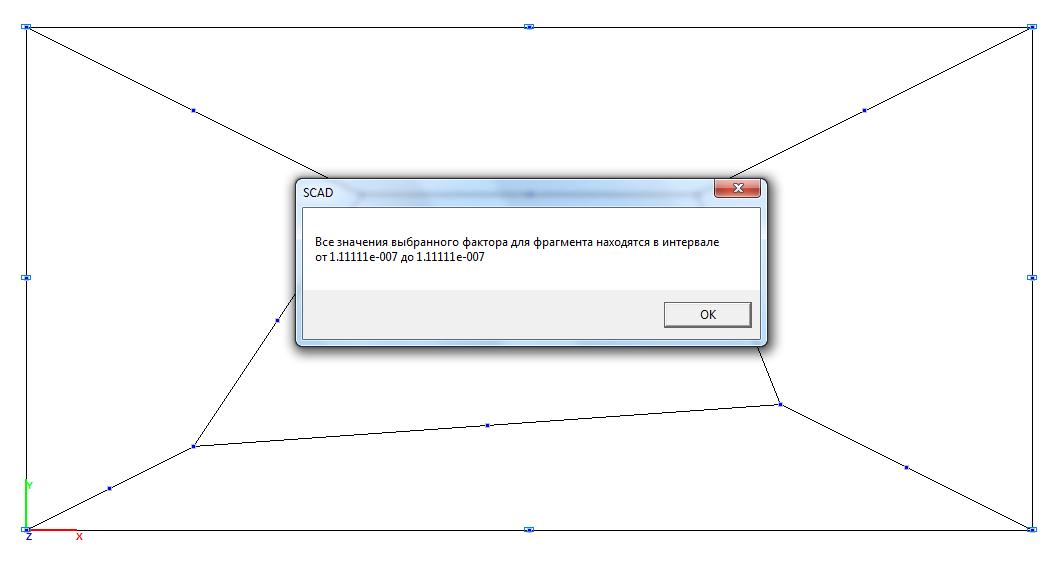
Model 4. Values of the bending moment M_x (kN∙m/m)

 

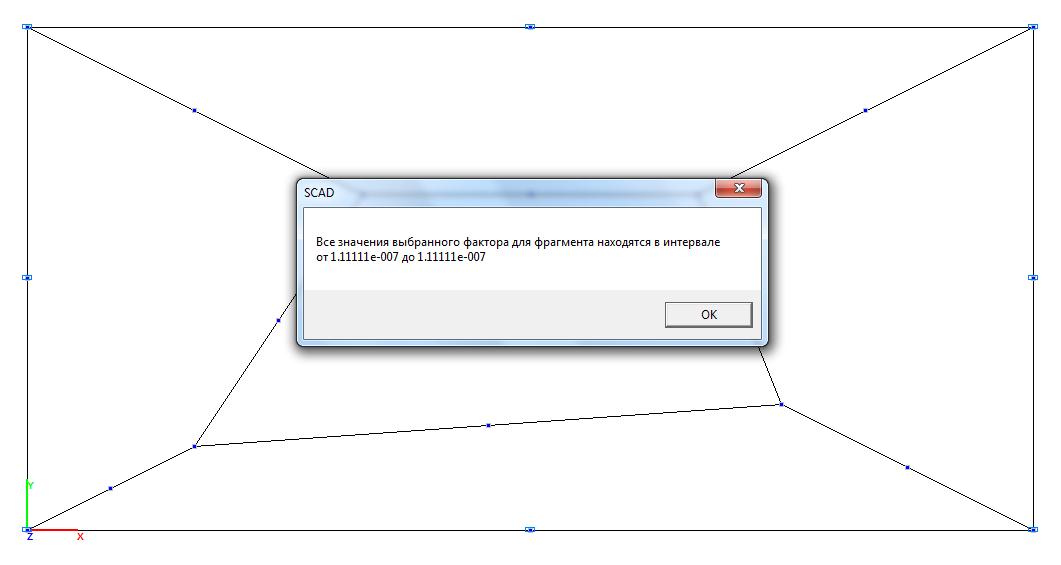
Model 4. Values of the bending moment M_y (kN∙m/m)

 

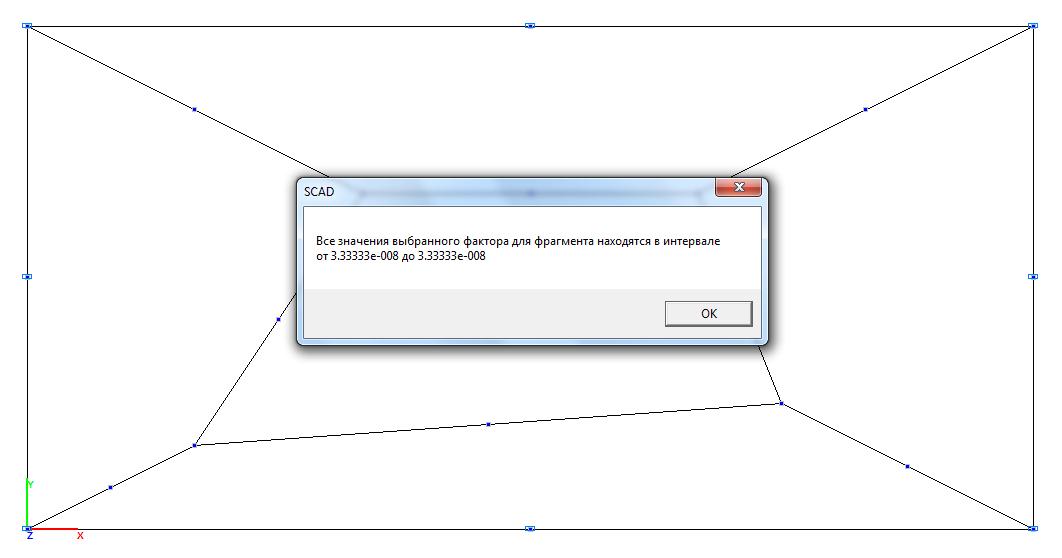
Model 4. Values of the torque M_xy (kN∙m/m)

 

 

Comparison of solutions:

Model	Parameter	Theory	SCAD	Deviation, %
1	Normal stresses σx, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Normal stresses σy, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Tangential stresses τxy, kN/m2	0.200	6∙0.333∙10-7/0.0012 = = 0.200	0.00
2	Normal stresses σx, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Normal stresses σy, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Tangential stresses τxy, kN/m2	0.200	6∙0.333∙10-7/0.0012 = = 0.200	0.00
3	Normal stresses σx, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Normal stresses σy, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Tangential stresses τxy, kN/m2	0.200	6∙0.333∙10-7/0.0012 = = 0.200	0.00
4	Normal stresses σx, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Normal stresses σy, kN/m2	0.667	6∙1.111∙10-7/0.0012 = = 0.667	0.00
	Tangential stresses τxy, kN/m2	0.200	6∙0.333∙10-7/0.0012 = = 0.200	0.00

Notes: In the analytical solution the normal σ_x, σ_y and tangential τ_xy stresses on the external surface of the plate are determined according to the following formulas:

\[ \sigma_{x} =10^{-3}\cdot \frac{E\cdot t}{2\cdot \left( {1-\nu } \right)}=\frac{6\cdot M_{x} }{t^{2}}; \quad \sigma_{y} =10^{-3}\cdot \frac{E\cdot t}{2\cdot \left( {1-\nu } \right)}=\frac{6\cdot M_{y} }{t^{2}}; \quad \\ \tau_{xy} =10^{-3}\cdot \frac{E\cdot t}{4\cdot \left( {1+\nu } \right)}=\frac{6\cdot M_{xy} }{t^{2}}. \]