SCAD: Pathological Tests

Curvilinear Cantilever Beam with Concentrated Shear Forces at Its Free End

Objective: Check of the obtained values of the transverse displacements of the free end of a curvilinear cantilever beam subjected to concentrated shear forces.

Initial data files:

File name

Description

Curved_cantilever_beam_Shell_42.spr

Design model with the elements of type 42

Curved_cantilever_beam_Shell_142.spr

Design model with the elements of type 142

Curved_cantilever_beam_Shell_44.spr

Design model with the elements of type 44

Curved_cantilever_beam_Shell_144.spr

Design model with the elements of type 144

Curved_cantilever_beam_Shell_45.spr

Design model with the elements of type 45

Curved_cantilever_beam_Shell_145.spr

Design model with the elements of type 145

Curved_cantilever_beam_Shell_50.spr

Design model with the elements of type 50

Curved_cantilever_beam_Shell_150.spr

Design model with the elements of type 150

Curved_cantilever_beam_Solid_36.spr

Design model with the elements of type 36

Curved_cantilever_beam_Solid_37.spr

Design model with the elements of type 37

 

Problem formulation: The curvilinear isotropic cantilever beam of a rectangular cross-section is subjected to the concentrated shear forces Py, Pz (bending in and out of the plane of the longitudinal axis of the beam) applied at its free end. Check the obtained values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam from the respective actions.

References: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.

Initial data:

E = 1.0·107 kPa - elastic modulus of the beam material;
ν = 0.25 - Poisson’s ratio;
b = 0. 1 m - width of the beam;
h = 0. 2 m - height of the beam;
R = 4.22 m - radius of the arc of the longitudinal axis of the beam;
α = π/2 rad - central angle of the arc of the longitudinal axis of the beam;
Py = 1.0 kN - value of the shear force acting along the height of the beam
(in the plane of the longitudinal axis);
Pz = 1.0 kN - value of the shear force acting along the width of the beam
(out of the plane of the longitudinal axis).
 

Finite element model: Design model – general type system. Ten design models with a trapezoidal finite element mesh are considered:

Model 1 - 12 three-node shell elements of type 42. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 14.

Model 2 - 12 three-node shell elements allowing for shear of type 142. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 14.

Model 3 - 6 four-node shell elements of type 44. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN).. Number of nodes in the model – 14.

Model 4 - 6 four-node shell elements allowing for shear of type 144. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 14.

Model 5 - 12 six-node shell elements of type 45. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 39.

Model 6 - 12 six-node shell elements allowing for shear of type 145. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 39.

Model 7 - 6 eight-node shell elements of type 50. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 33.

Model 8 - 6 eight-node shell elements allowing for shear of type 150. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of two nodal forces (Py = 2∙0.5 kN, Pz = 2∙0.5 kN). Number of nodes in the model – 33.

Model 9 - 6 eight-node isoparametric solid elements of type 36. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of four nodal forces (Py = 4∙0.25 kN, Pz = 4∙0.25 kN). Number of nodes in the model – 28.

Model 10 - 6 twenty-node isoparametric solid elements of type 37. Boundary conditions are provided by imposing constraints on the nodes of the clamped end of the beam in the directions of the degrees of freedom X, Y, Z, UX, UY, UZ. The concentrated shear Py, Pz forces are given in the form of four nodal forces (Py = 4∙0.25 kN, Pz = 4∙0.25 kN). Number of nodes in the model – 80.

 

Results in SCAD


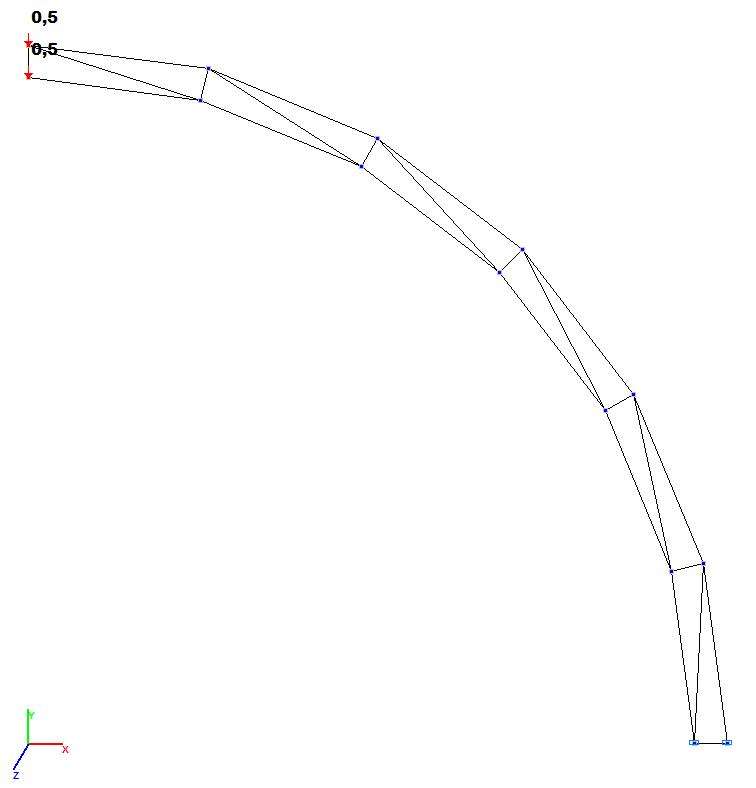
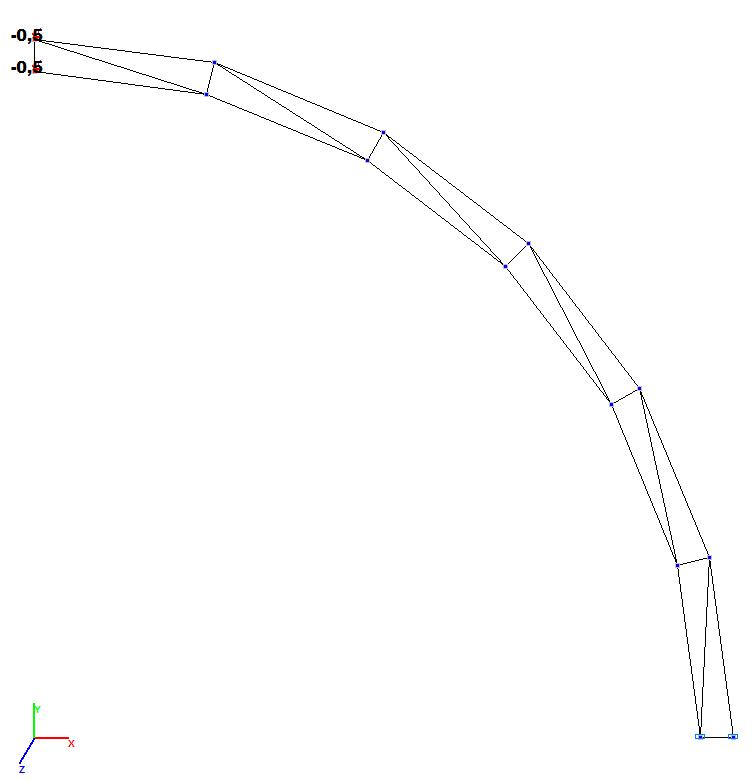
Models 1 and 2. Design model

 


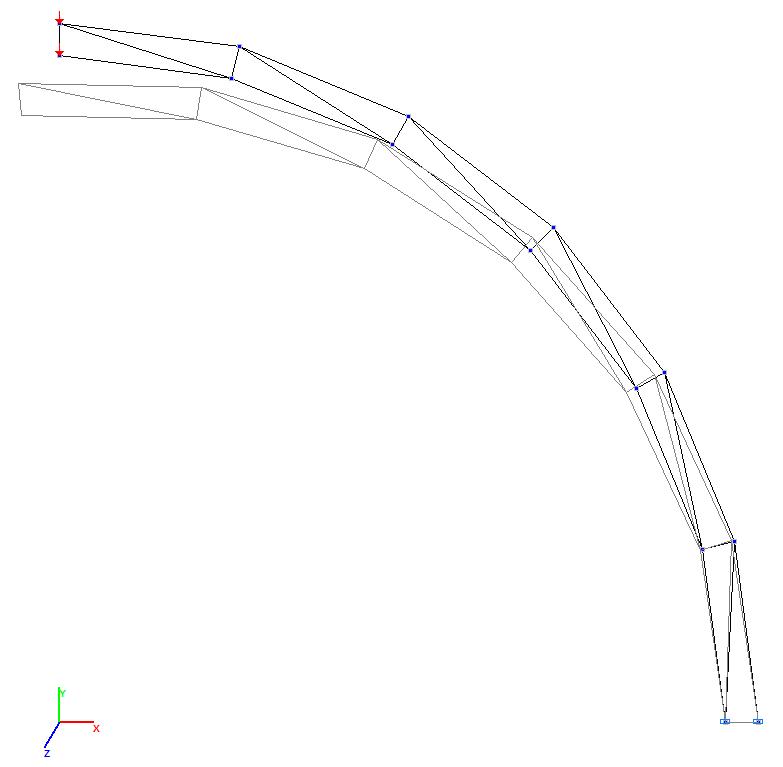
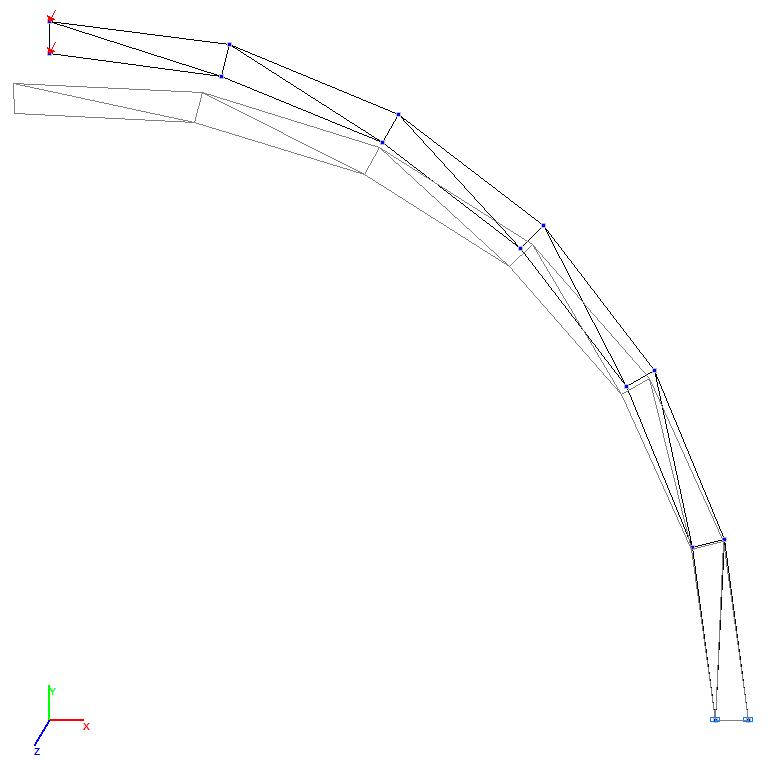
Models 1 and 2. Deformed model

 


Model 1. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


Model 2. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


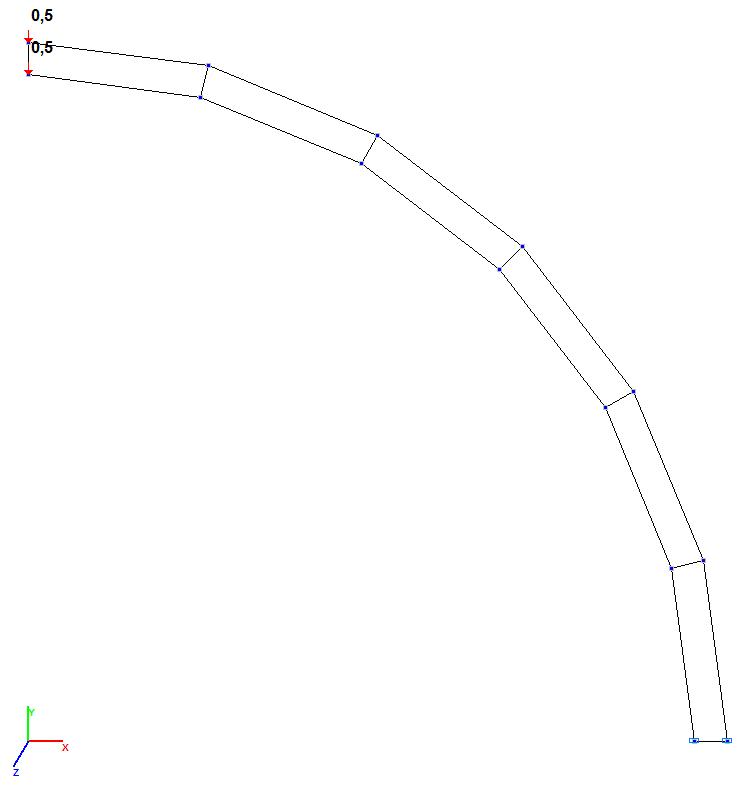
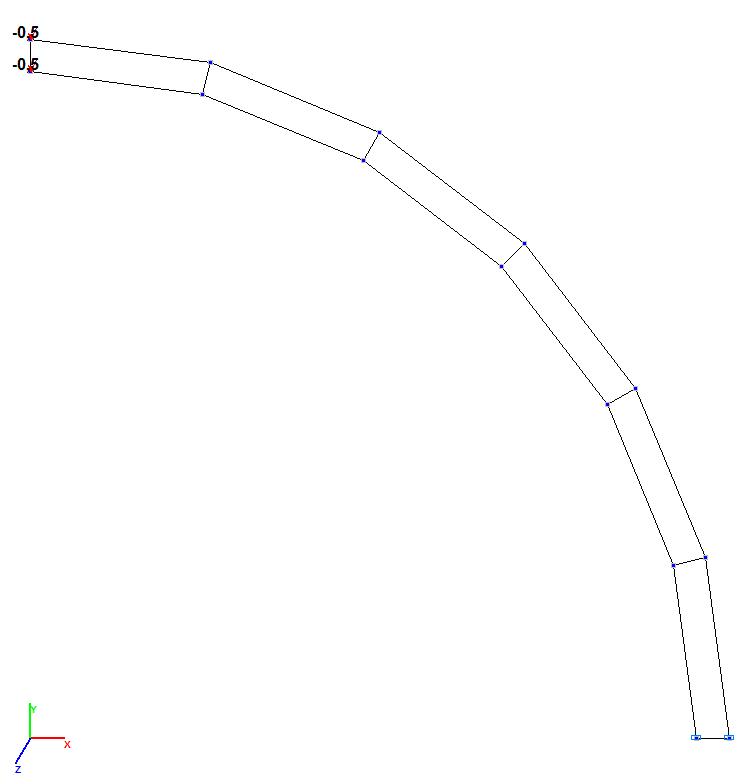
Models 3 and 4. Design model

 

 


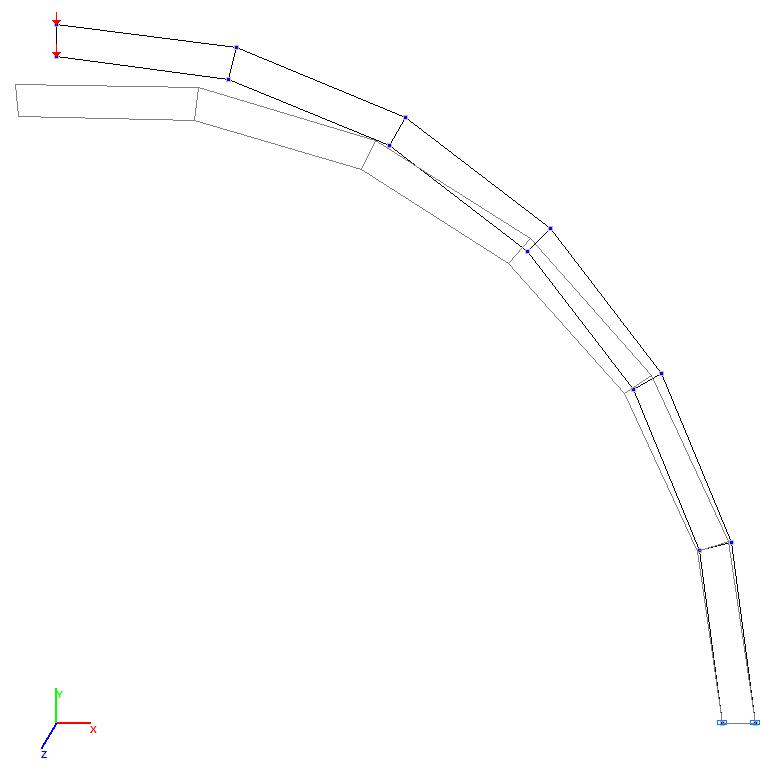
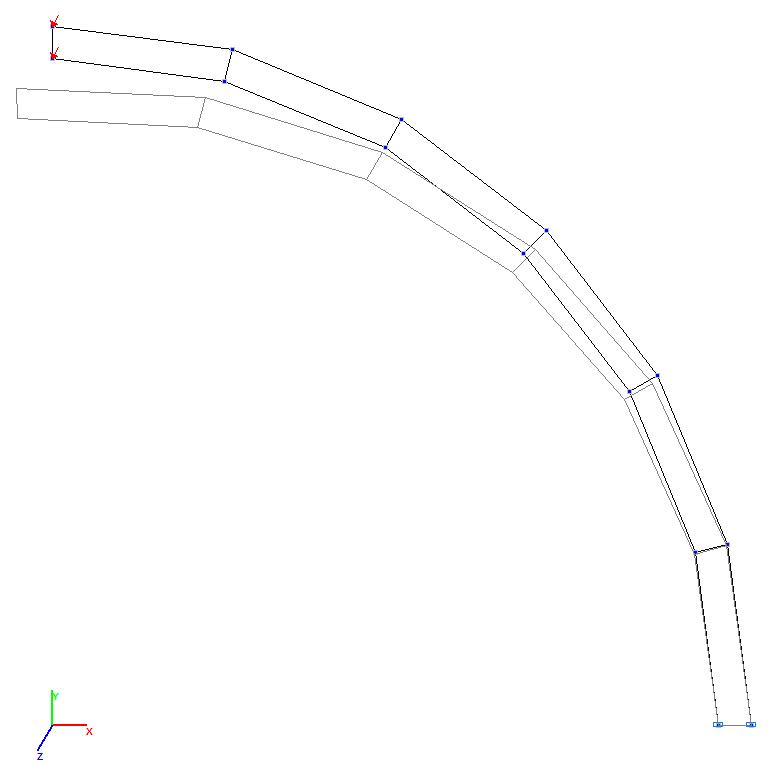
Models 3 and 4. Deformed model

 


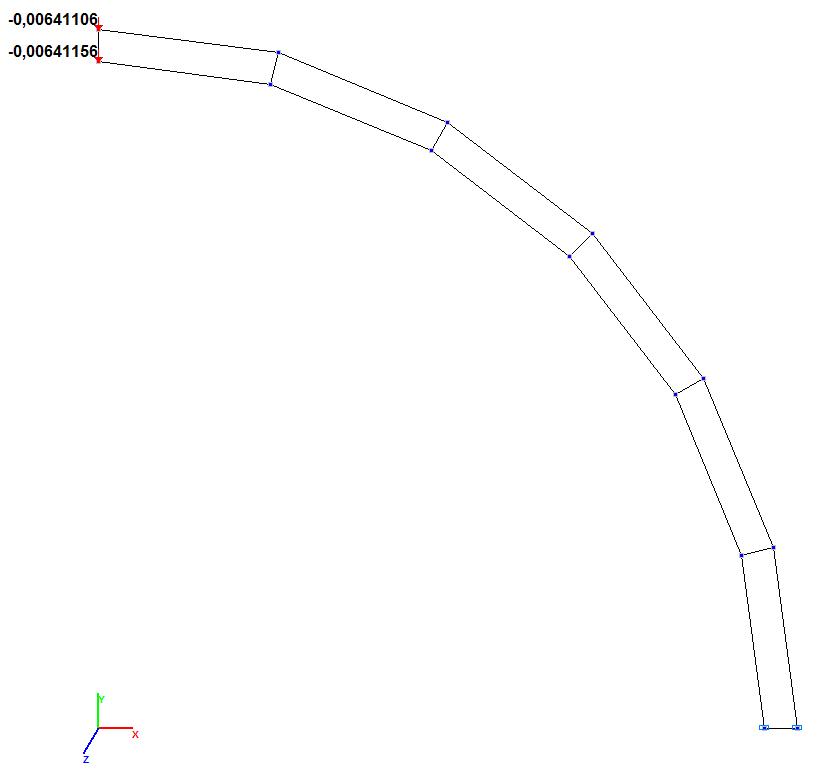
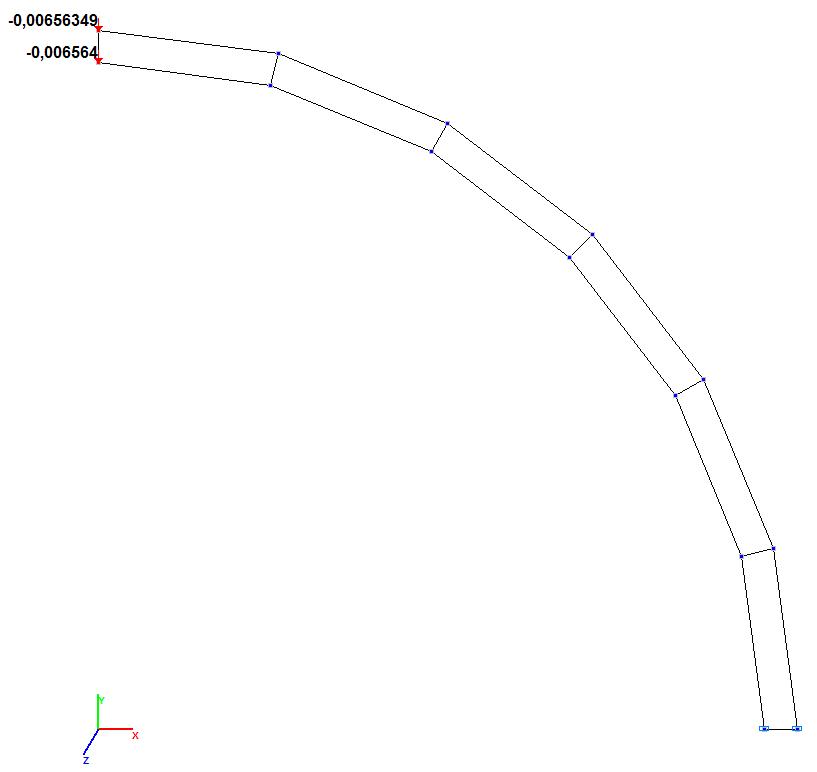
Model 3. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


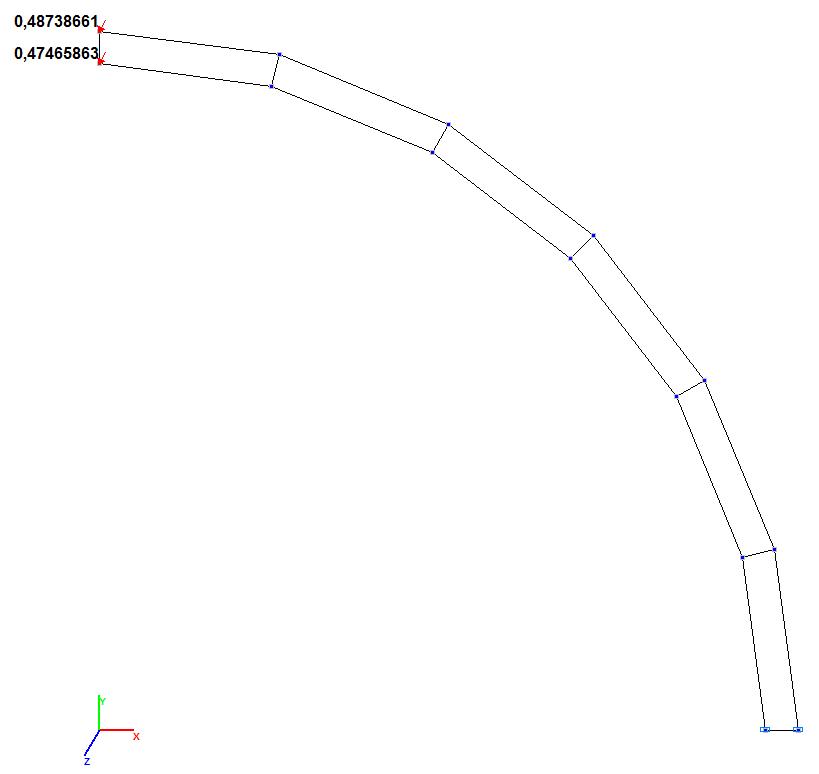
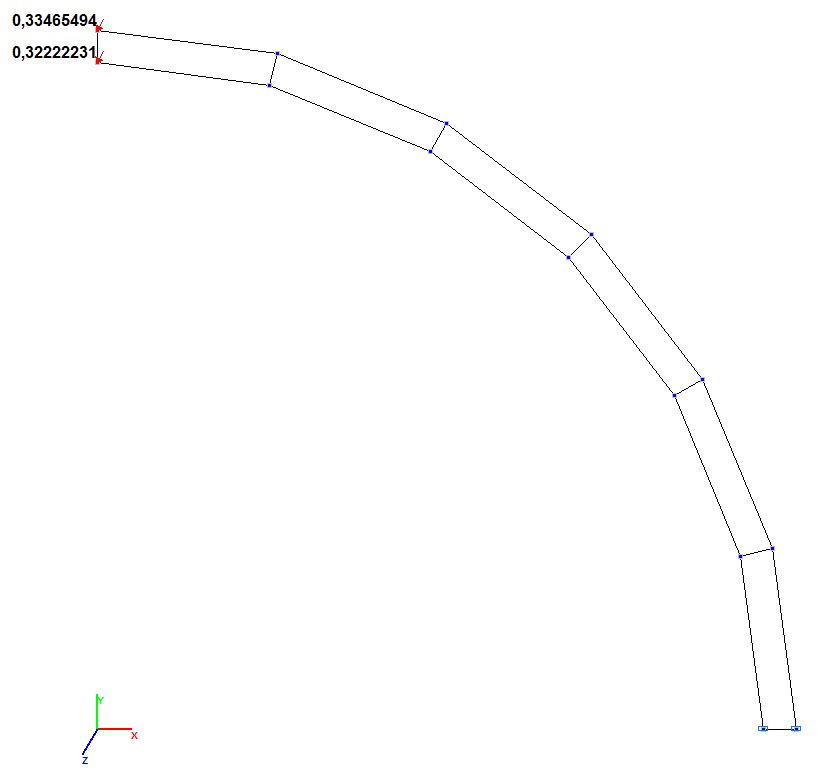
Model 4. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


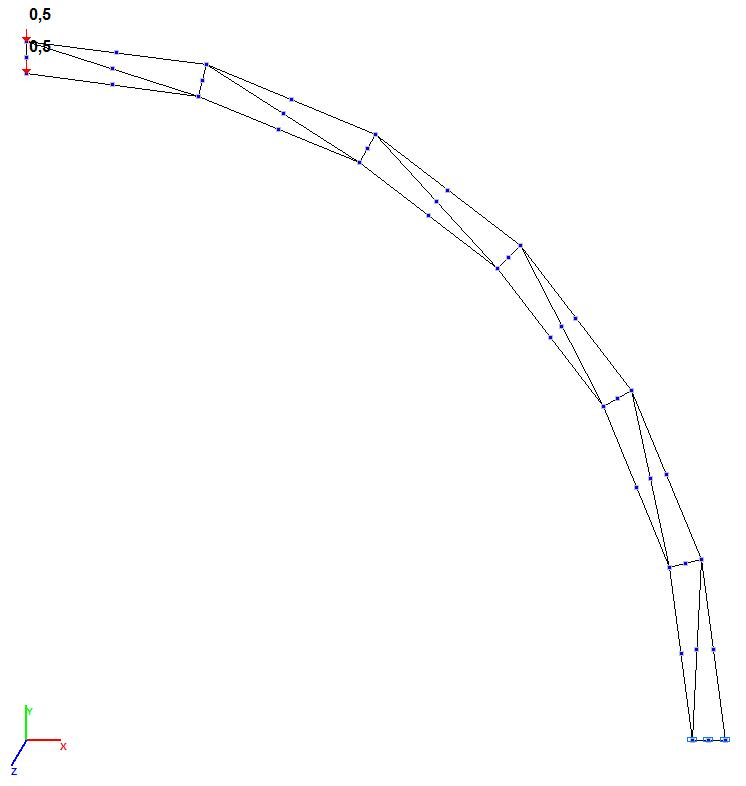
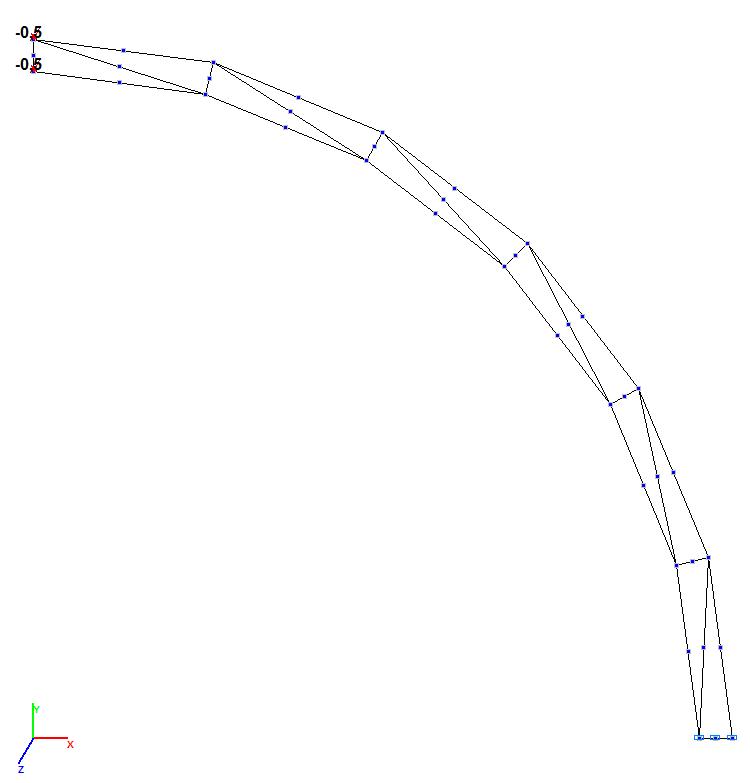
Models 5 and 6. Design model

 


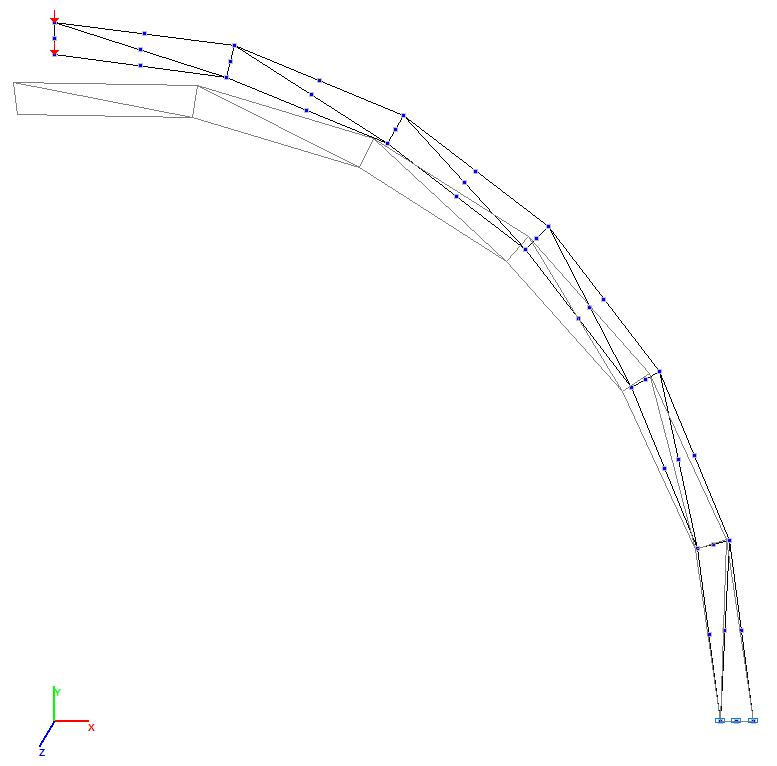
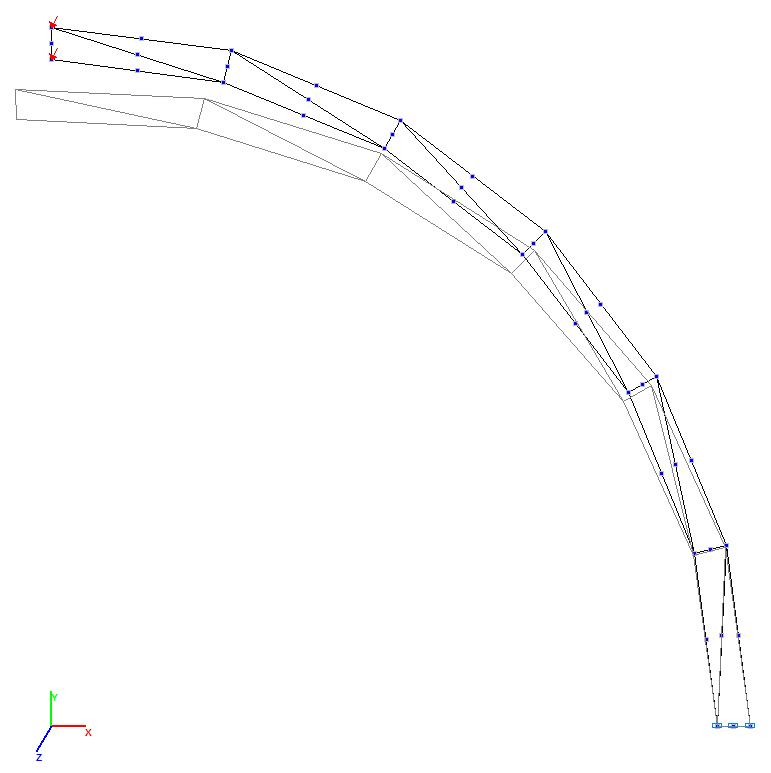
Models 5 and 6. Deformed model

 


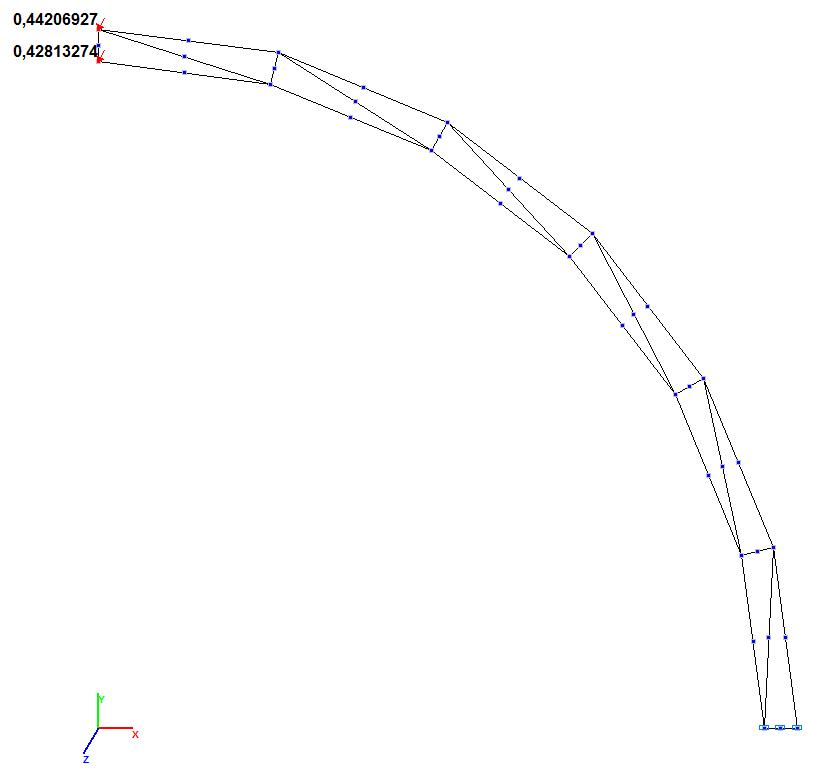
Model 5. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


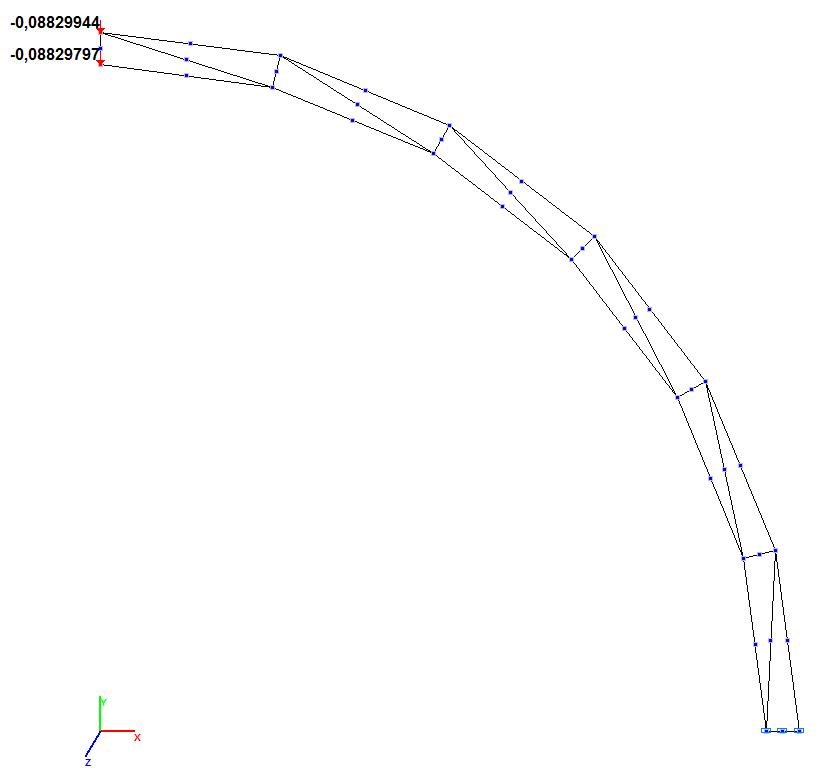
Model 6. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


Models 7 and 8. Design model

 


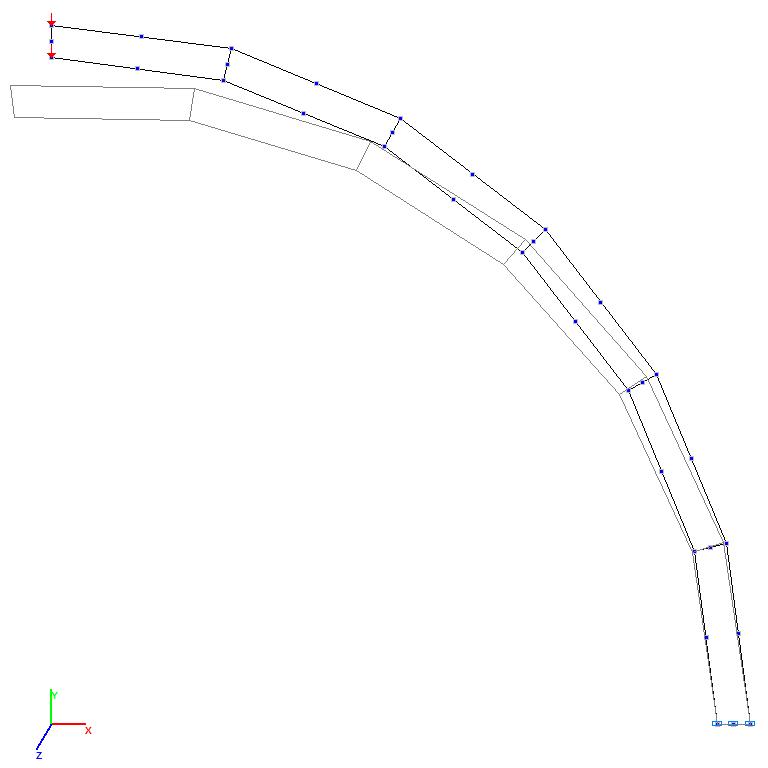
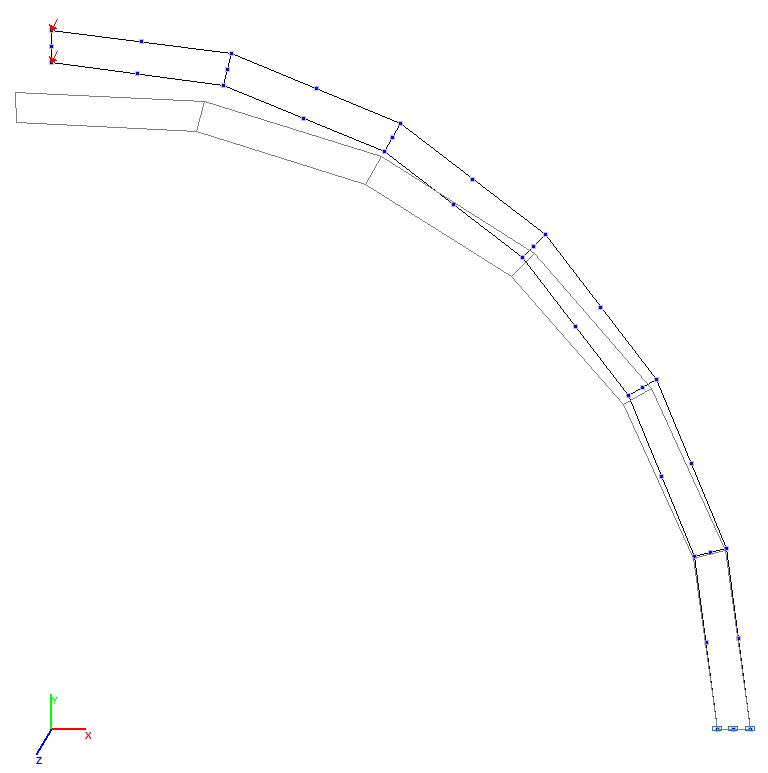
Mоdels 7 and 8. Deformed model

 


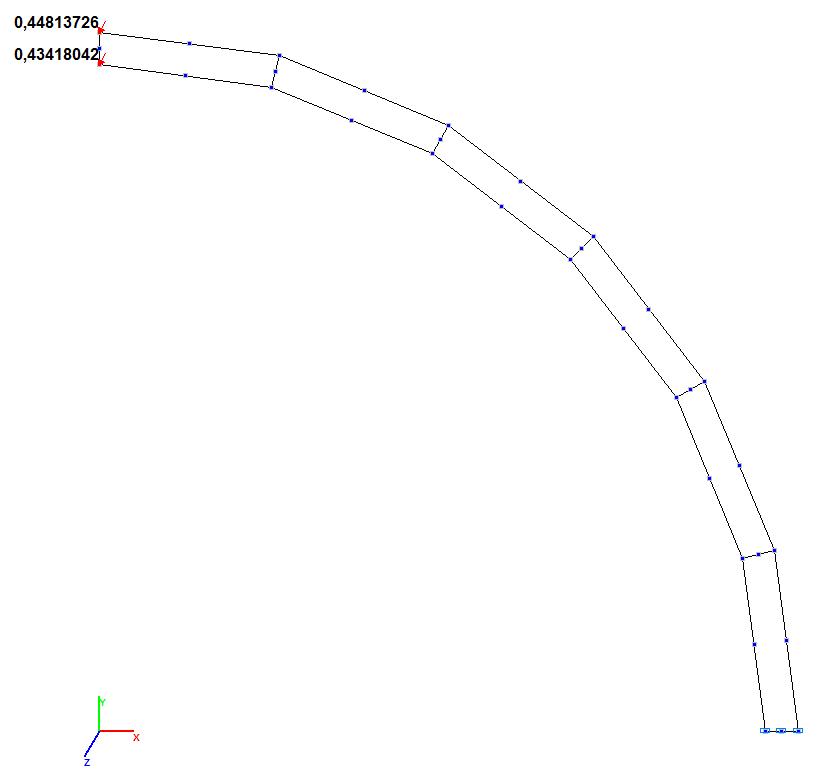
Model 7. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


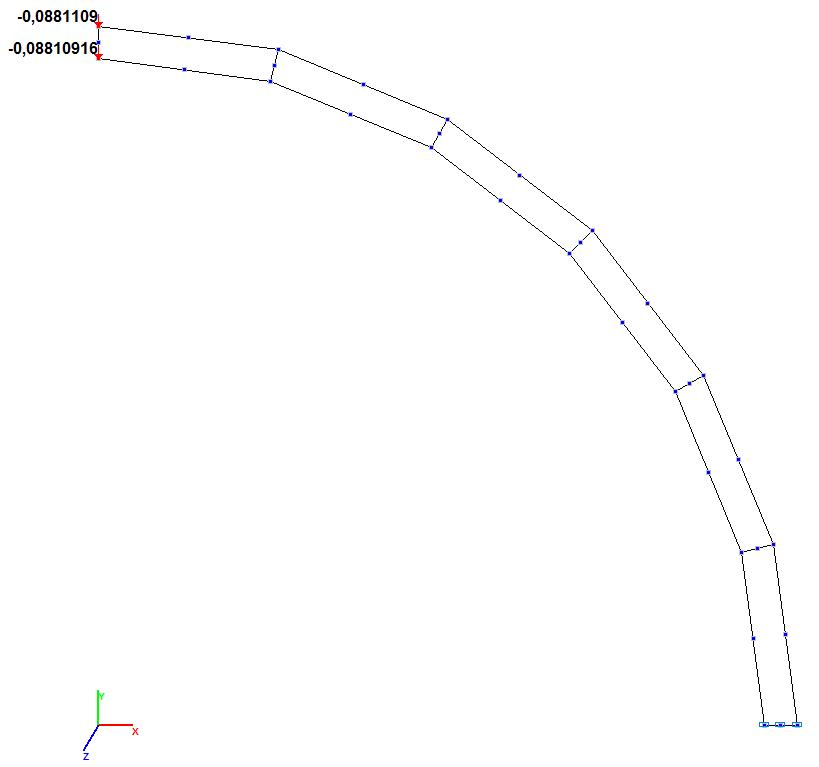
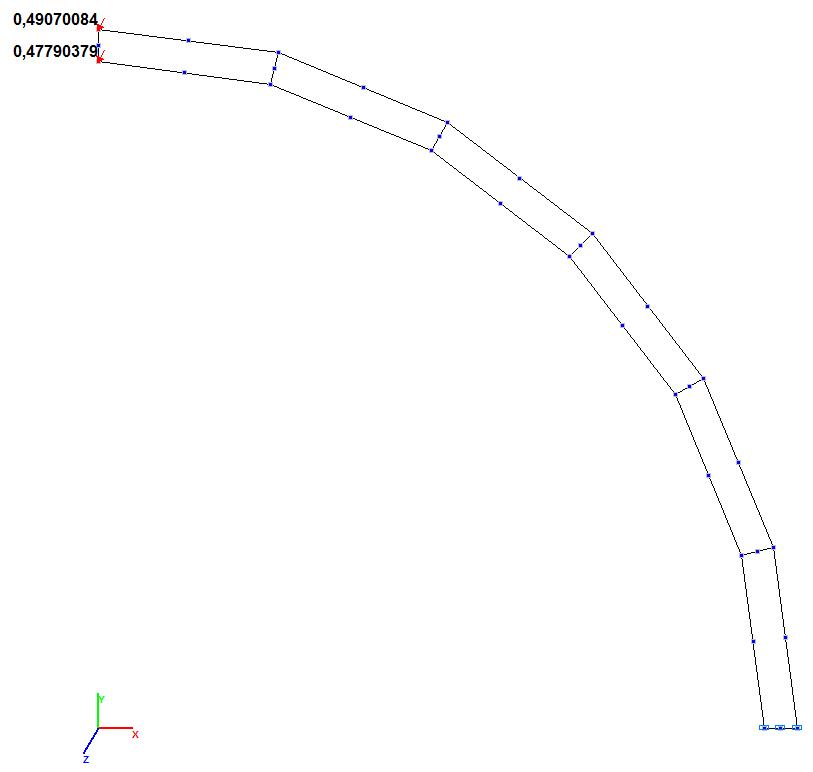
Model 8. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


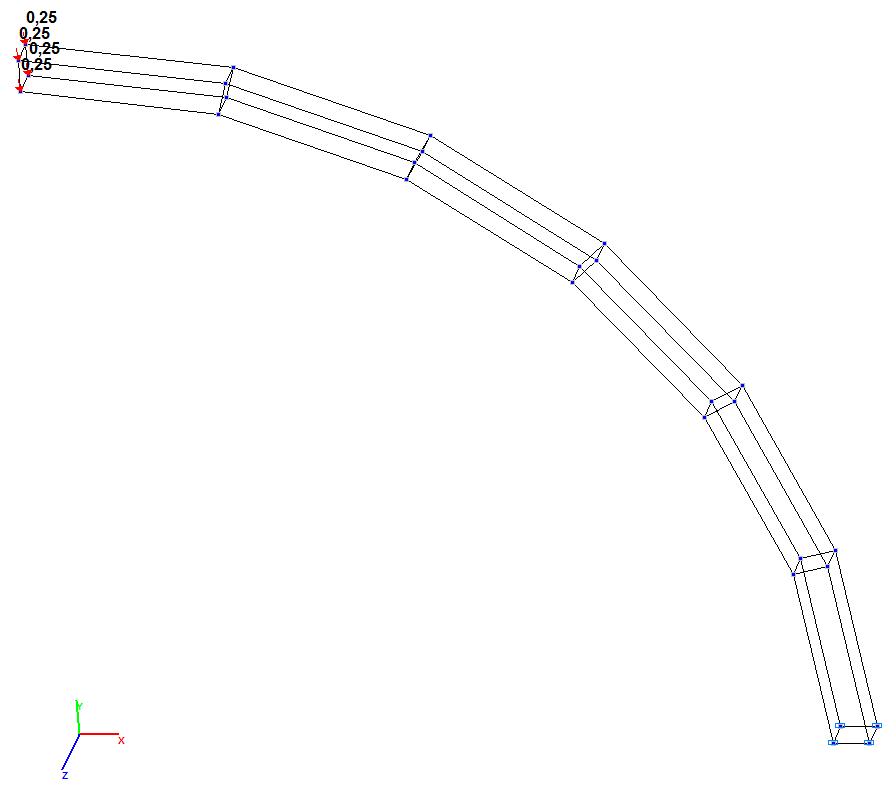
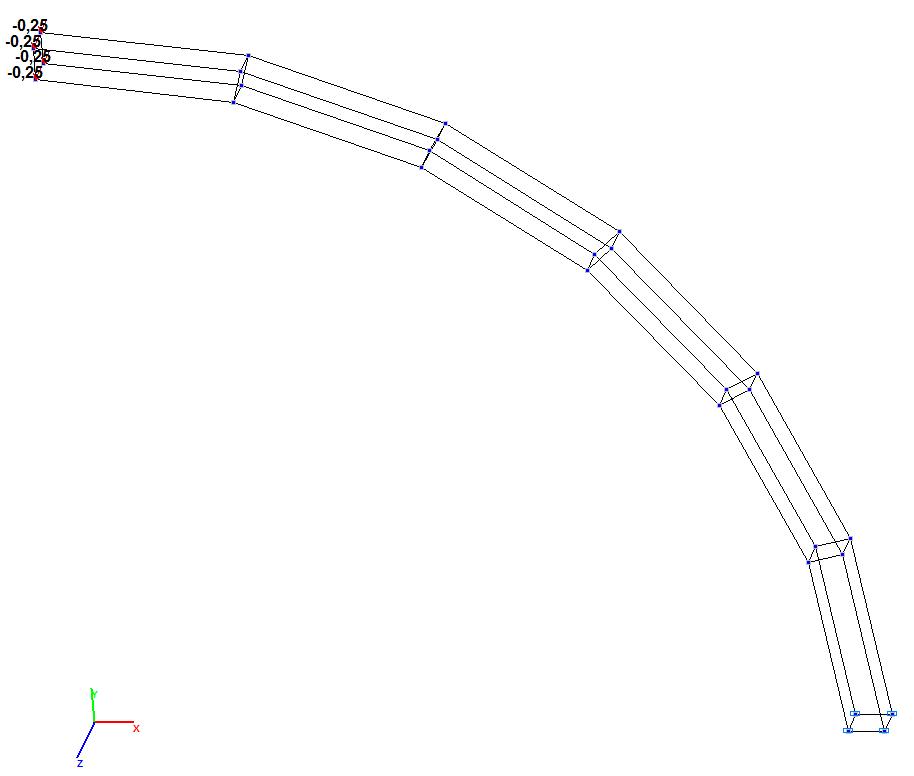
Model 9. Design model

 


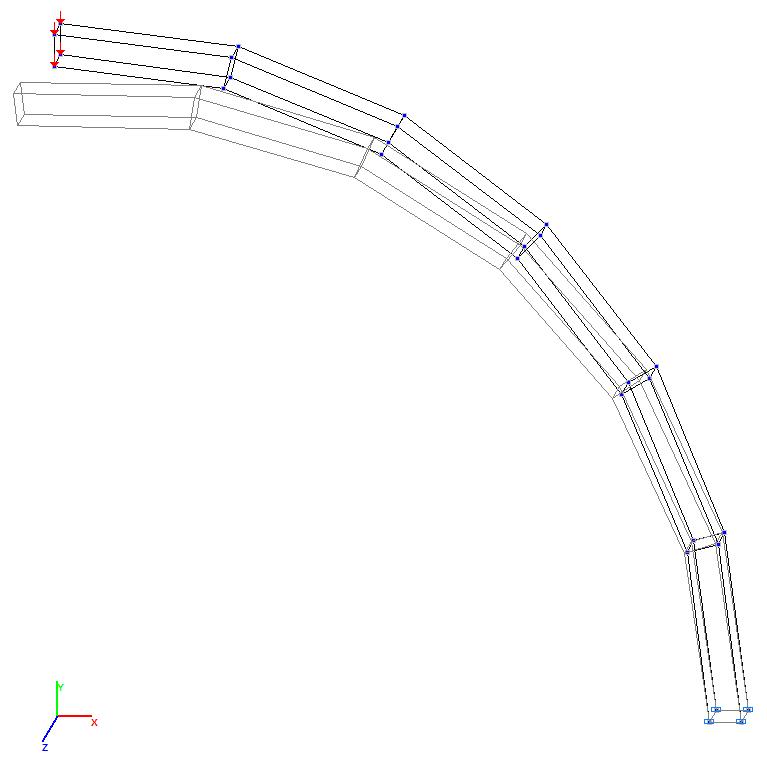
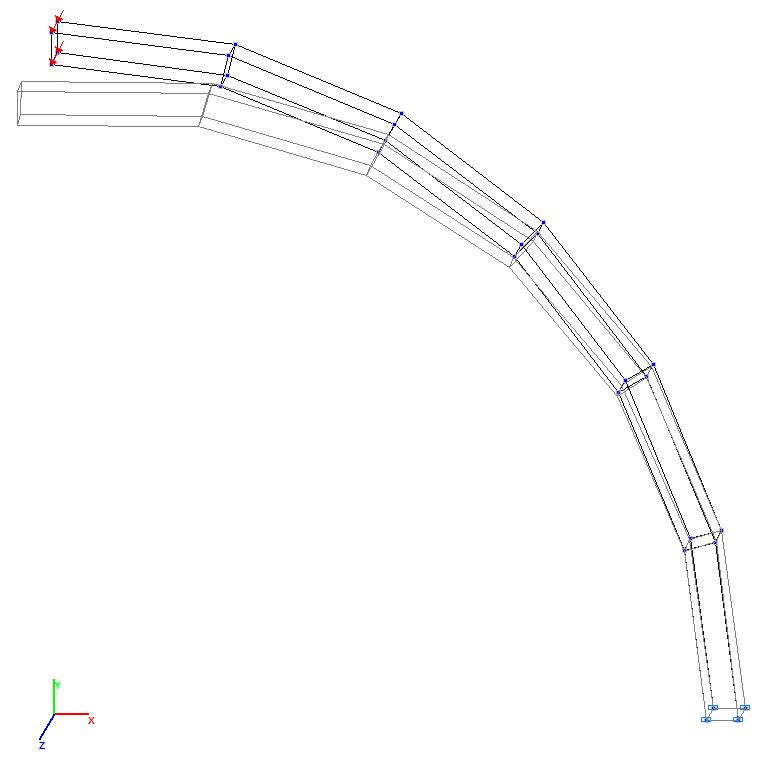
Model 9. Deformed model

 


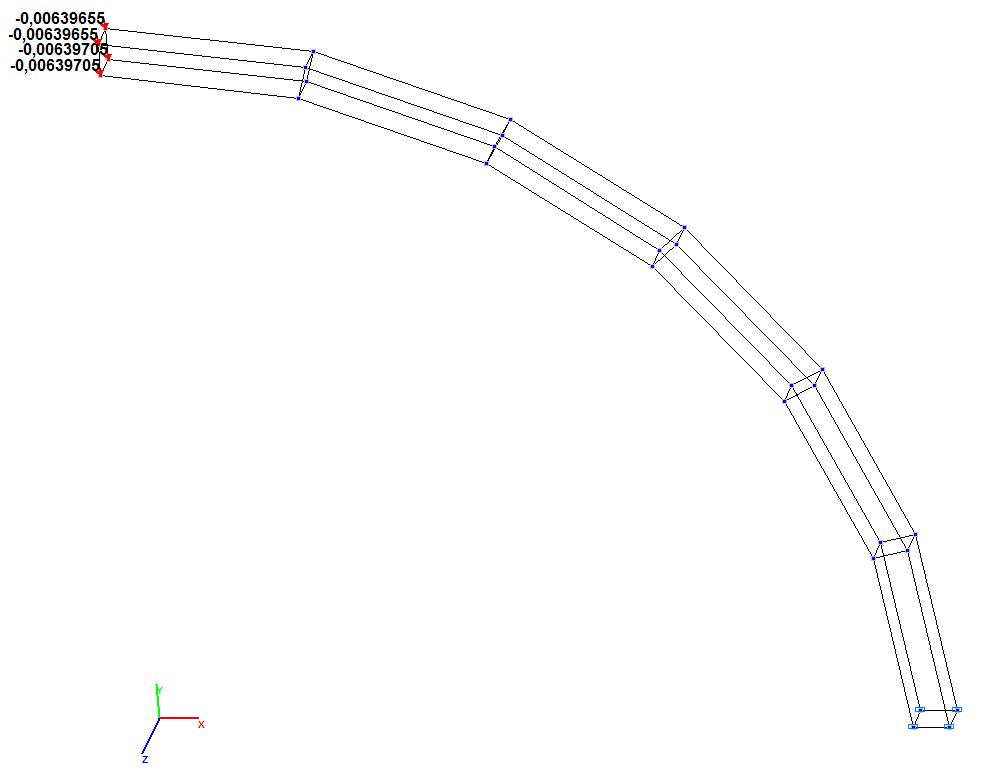
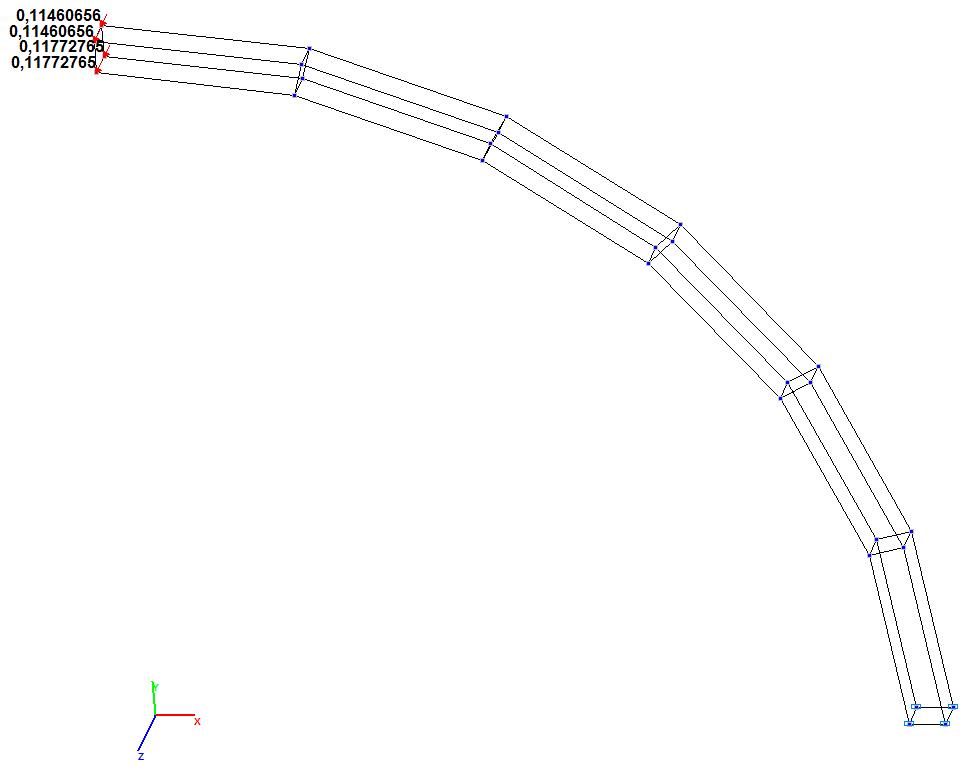
Model 9. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 


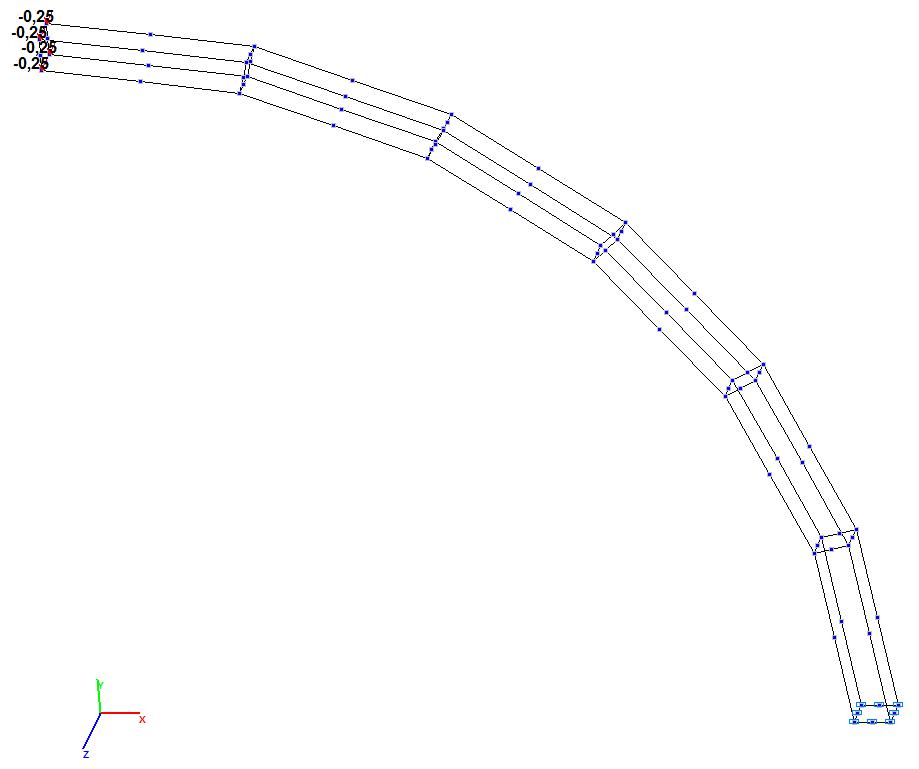
Model 10. Design model

 


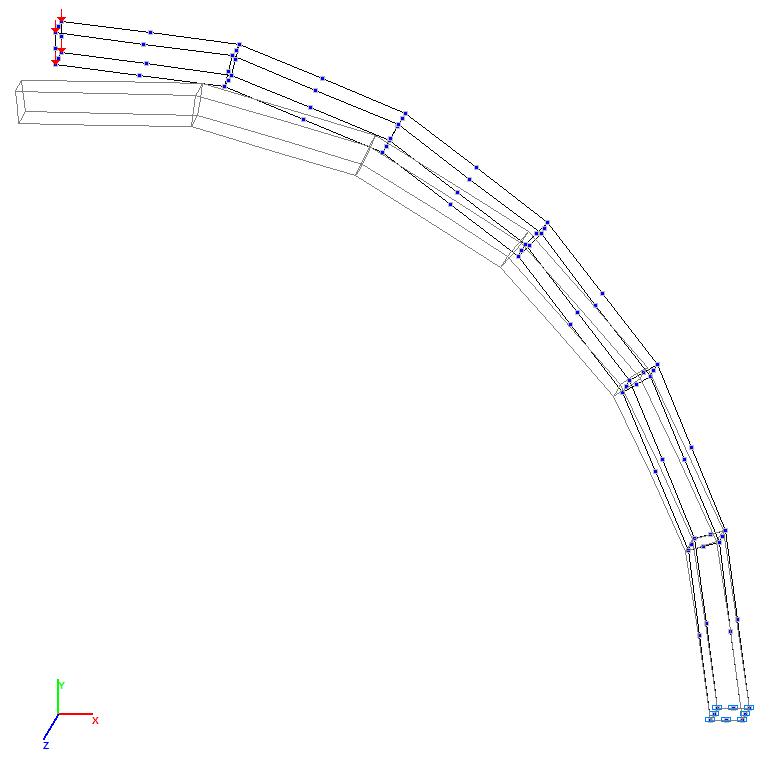
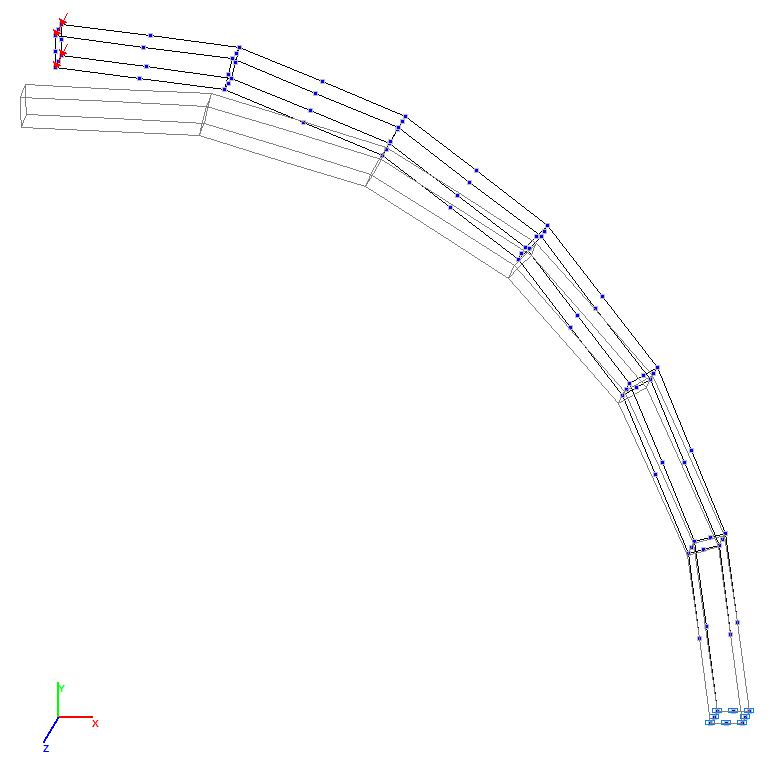
Model 10. Deformed model

 


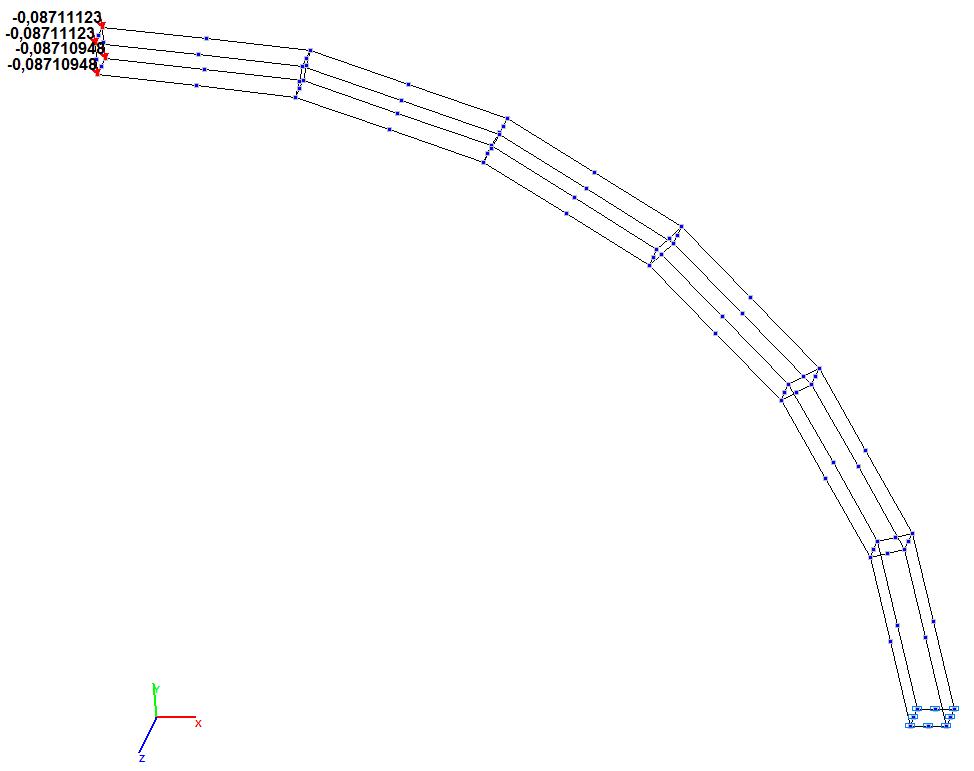
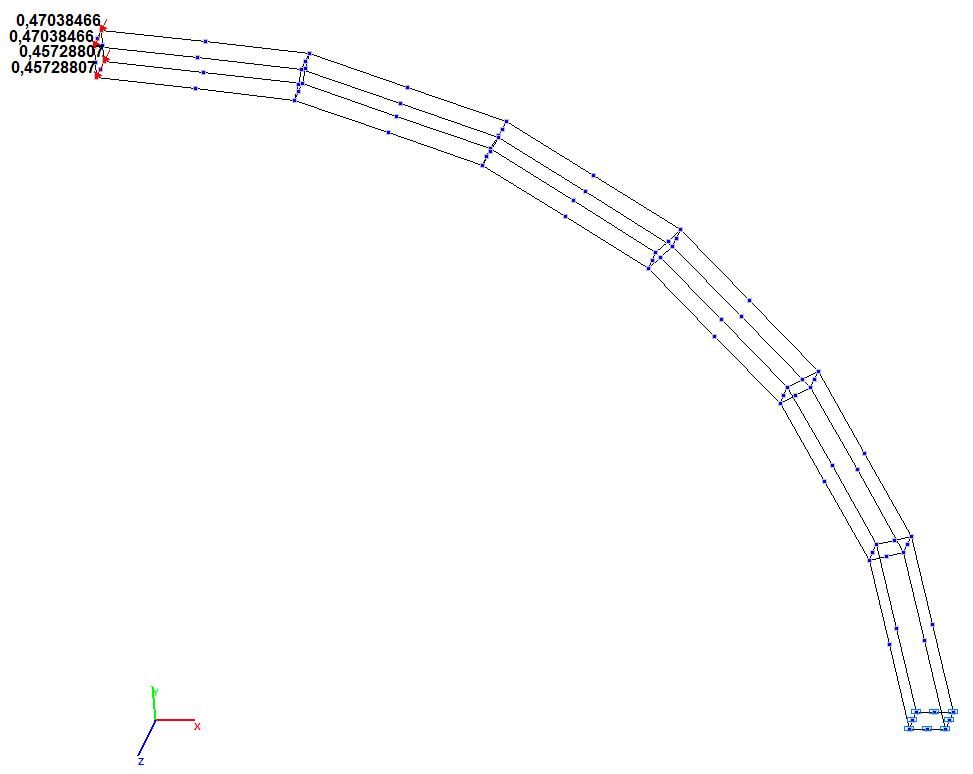
Model 10. Values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam (m, m)

 

Comparison of solutions:

Model

Parameter

Theory

SCAD

Deviation, %

1

(Member type 42)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.002213

97.50

Transverse displacement Z of the free end of the cantilever beam, m

0.454527*

0.308152

32.20

2

(Member type 142)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.02213

97.50

Transverse displacement Z of the free end of the cantilever beam, m

0.500466

0.474844

5.12

3

(Member type 44)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.006411

92.76

Transverse displacement Z of the free end of the cantilever beam, m

0.454527*

0.334655

26.37

4

(Member type 144)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.006563

92.59

Transverse displacement Z of the free end of the cantilever beam, m

0.500466

0.487387

2.61

5

(Member type 45)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.088299

0.27

Transverse displacement Z of the free end of the cantilever beam, m

0.454527*

0.442069

2.74

6

(Member type 145)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.088299

0.27

Transverse displacement Z of the free end of the cantilever beam, m

0.500466

0.487623

2.57

7

(Member type 50)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.088111

0.48

Transverse displacement Z of the free end of the cantilever beam, m

0.454527*

0.448137

1.41

8

(Member type 150)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.088111

0.48

Transverse displacement Z of the free end of the cantilever beam, m

0.500466

0.490701

1.95

9

(Member type 36)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.006397

92.77

Transverse displacement Z of the free end of the cantilever beam, m

0.500466

0.114607

77.10

10

(Member type 37)

Transverse displacement Y of the free end of the cantilever beam, m

0.088536

0.087111

1.61

Transverse displacement Z of the free end of the cantilever beam, m

0.500466

0.470384

6.01

* The values of the transverse displacements Z for thin plates (not allowing for shear) are determined at the free torsional inertia moment calculated with the value of the coefficient kf, equal to 1/3 (h/b = ∞).

 

Notes: In the analytical solution the values of the transverse displacements Y, Z of the free end of the curvilinear cantilever beam from the respective actions are determined according to the following formulas:

\[ Y=\frac{3\cdot \pi \cdot P_{y} \cdot R^{3}}{E\cdot b\cdot h^{3}}; \quad Z=\frac{P_{z} \cdot R^{3}}{2\cdot E\cdot b^{3}\cdot h\cdot k_{f} }\cdot \left[ {6\cdot \pi \cdot k_{f} +\left( {3\cdot \pi -8} \right)\cdot \left( {1+\nu } \right)} \right], \] \[ where: \quad k_{f} =\frac{1}{3}\cdot \left\{ {1-\frac{192}{\pi^{5}}\cdot \frac{b}{h}\cdot \sum\limits_{n=1}^\infty {\left[ {\sin^{2}\left( {\frac{n\cdot \pi }{2}} \right)\cdot \frac{1}{n^{5}}\cdot th\left( {\frac{n\cdot \pi \cdot h}{2\cdot b}} \right)} \right]} } \right\}. \]