Three-Step Simply Supported Beam Subjected to Concentrated Forces

Objective: Strain state of a three-step simply supported beam subjected to concentrated forces without taking into account the transverse shear deformations. Transverse displacements and rotation angles are checked.

Initial data file: 4_5.spr

Problem formulation: The three-step simply supported beam is subjected to three concentrated forces Р. Determine the rotation angles of support sections and transverse displacements in the force application points.

References: G.S. Pisarenko, A.P. Yakovlev, V.V. Matveev, Handbook on Strength of Materials. — Kiev: Naukova Dumka, 1988.

Initial data:

E = 2.0·1011  Pa	- elastic modulus,
l = 1 m	- half length of the beam span of each section;
F = 1·10-2 m2	- cross-sectional area;
I1  = 5·10-6 m4	- moment of inertia;
Р = 1 kN	- load value.
I1 : I2 : I3 = 1 : 2 : 3
F1 : F2 :F3 = 1 : 2 : 3

 

Finite element model: Design model – general type system, 6 bar elements of type 5, 7 nodes.

Results in SCAD

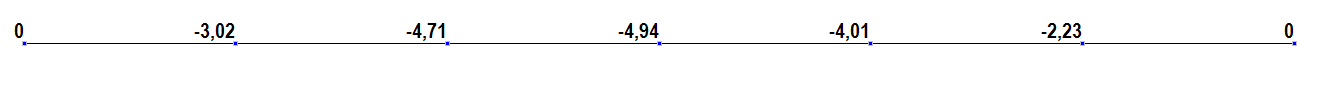
Values of transverse displacements w (mm)

Values of rotation angles θ (rad)

Comparison of solutions:

Parameter	Theory	SCAD	Deviations, %
Transverse displacements, mm w  (l) w  (3l) w  (5l)	-3.02 -4.94 -2.23	-3.02 -4.94 -2.23	0.00 0.00 0.00
Rotation angles, rad θ (0) θ (6l)	0.00327 -0.00231	0.00327 -0.00231	0.00 0.00

Notes: In the analytical solution, the rotation angles of support sections and deflections in the force application points are determined according to the following formulas:

\[ w\left( l \right)=-\frac{653\cdot P\cdot l^{3}}{216\cdot E\cdot I_{1} }; \quad w\left( {3\cdot l} \right)=-\frac{89\cdot P\cdot l^{3}}{18\cdot E\cdot I_{1} }; \quad w\left( {5\cdot l} \right)=-\frac{481\cdot P\cdot l^{3}}{216\cdot E\cdot I_{1} }; \] \[ \theta \left( 0 \right)=\frac{707\cdot P\cdot l^{2}}{216\cdot E\cdot I_{1} }; \quad \theta \left( {6\cdot l} \right)=-\frac{499\cdot P\cdot l^{2}}{216\cdot E\cdot I_{1} }. \]