Open Cylindrical Shell Rectangular in Plan and Simply Supported along the Curvilinear Edges Subjected to a Transverse Load Uniformly Distributed over the Entire Area
Objective: Check of the obtained values of the transverse displacements in the middle of the free rectilinear edges of an open cylindrical shell rectangular in plan and simply supported along the curvilinear edges subjected to a transverse load uniformly distributed over the entire area.
Initial data files:
|
File name |
Description |
|---|---|
|
Design model with the elements of type 42 for meshes 2x2, 4x4, 8x8 |
|
|
Design model with the elements of type 44 for meshes 2x2, 4x4, 8x8 |
|
|
Design model with the elements of type 45 for meshes 2x2, 4x4, 8x8 |
|
|
Design model with the elements of type 50 for meshes 2x2, 4x4, 8x8 |
|
|
Scordelis-Lo_roof _ Solid _36.SPR _Mesh_16x16.SPR Scordelis-Lo_roof _ Solid _36.SPR _Mesh_32x32.SPR Scordelis-Lo_roof _ Solid _36.SPR _Mesh_64x64.SPR Scordelis-Lo_roof _ Solid _36.SPR _Mesh_128x128.SPR |
Design model with the elements of type 36 for meshes 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 |
|
Scordelis-Lo_roof _ Solid _37.SPR _Mesh_16x16.SPR Scordelis-Lo_roof _ Solid _37.SPR _Mesh_32x32.SPR Scordelis-Lo_roof _ Solid _37.SPR _Mesh_64x64.SPR Scordelis-Lo_roof _ Solid _37.SPR _Mesh_128x128.SPR |
Design model with the elements of type 37 for meshes 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 |
Problem formulation: The open cylindrical shell rectangular in plan and simply supported along the curvilinear edges by ideal end diaphragms rigid in their plane and compliant out of their plane is subjected to the transverse load q uniformly distributed over the entire area. Check the obtained values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq.
References: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.
A. C. Scordelis, K. S. Lo, Computer analysis of cylindrical shells, Journal of the American concrete institute, Title No 61-33, May 1964, p. 539-561.
Design of cylindrical concrete shell roofs, New York, Manual No 31 American society of civil engineers, 1952.
Initial data:
| E = 4.32·108 kPa | - elastic modulus of the material of the cylindrical shell; |
| ν = 0.00 | - Poisson’s ratio; |
| L = 50.00 m | - length of the generatrix of the cylindrical shell;; |
| R = 25.00 m | - radius of the midsurface of the cylindrical shell; |
| 2•θ = 2•40° | - central angle of the arc of the director of the cylindrical shell; |
| h = 0.25 m | - thickness of the cylindrical shell; |
| q = 90.0 kN/m2 | - value of the transverse load uniformly distributed over the entire area of the cylindrical shell. |
Finite element model: Design model – general type system. Six design models of a quarter of the cylindrical shell according to the symmetry conditions are considered:
Model 1 – 8, 32, 128 three-node shell elements of type 42 with a regular mesh 2x2, 4x4, 8x8. Boundary conditions are provided by imposing constraints on the nodes of the support curvilinear edges of the cylindrical shell in the directions of the degrees of freedom X, Z and constraints according to the symmetry conditions. Number of nodes in the model – 9, 25, 81.
Model 2 – 4, 16, 64 four-node shell elements of type 44 with a regular mesh 2x2, 4x4, 8x8. Boundary conditions are provided by imposing constraints on the nodes of the support curvilinear edges of the cylindrical shell in the directions of the degrees of freedom X, Z and constraints according to the symmetry conditions. Number of nodes in the model – 9, 25, 81.
Model 3 – 8, 32, 128 six-node shell elements of type 45 with a regular mesh 2x2, 4x4, 8x8. Boundary conditions are provided by imposing constraints on the nodes of the support curvilinear edges of the cylindrical shell in the directions of the degrees of freedom X, Z and constraints according to the symmetry conditions. Number of nodes in the model – 25, 81, 289.
Model 4 – 4, 16, 64 eight-node shell elements of type 50 with a regular mesh 2x2, 4x4, 8x8. Boundary conditions are provided by imposing constraints on the nodes of the support curvilinear edges of the cylindrical shell in the directions of the degrees of freedom X, Z and constraints according to the symmetry conditions. Number of nodes in the model – 25, 81, 289.
Model 5 – 4, 16, 64, 256, 1024, 4096, 16384 eight-node isoparametric solid elements of type 36 with a regular mesh 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Boundary conditions are provided by imposing constraints on the nodes of the support curvilinear sides of the cylindrical shell in the directions of the degrees of freedom X, Z and constraints according to the symmetry conditions. Number of nodes in the model – 18, 50, 162, 578, 2178, 8450, 33282.
Model 6 – 4, 16, 64, 256, 1024, 4096, 16384 twenty-node isoparametric solid elements of type 37 with a regular mesh 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Boundary conditions are provided by imposing constraints on the nodes of the support curvilinear sides of the cylindrical shell in the directions of the degrees of freedom X, Z and constraints according to the symmetry conditions. Number of nodes in the model – 51, 155, 531, 1955, 7491, 29315, 115971.
Results in SCAD
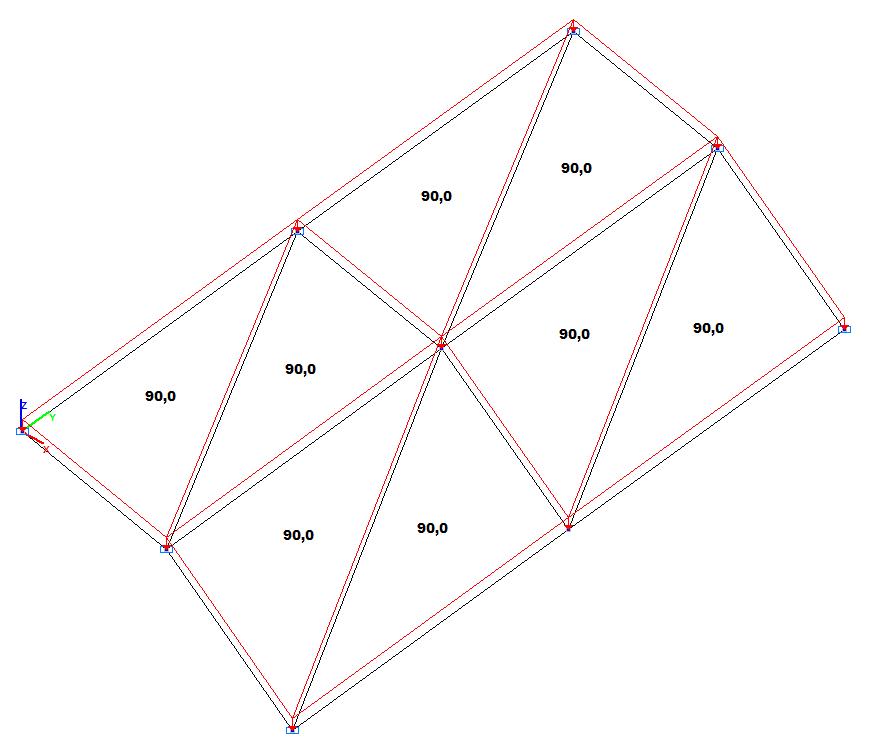
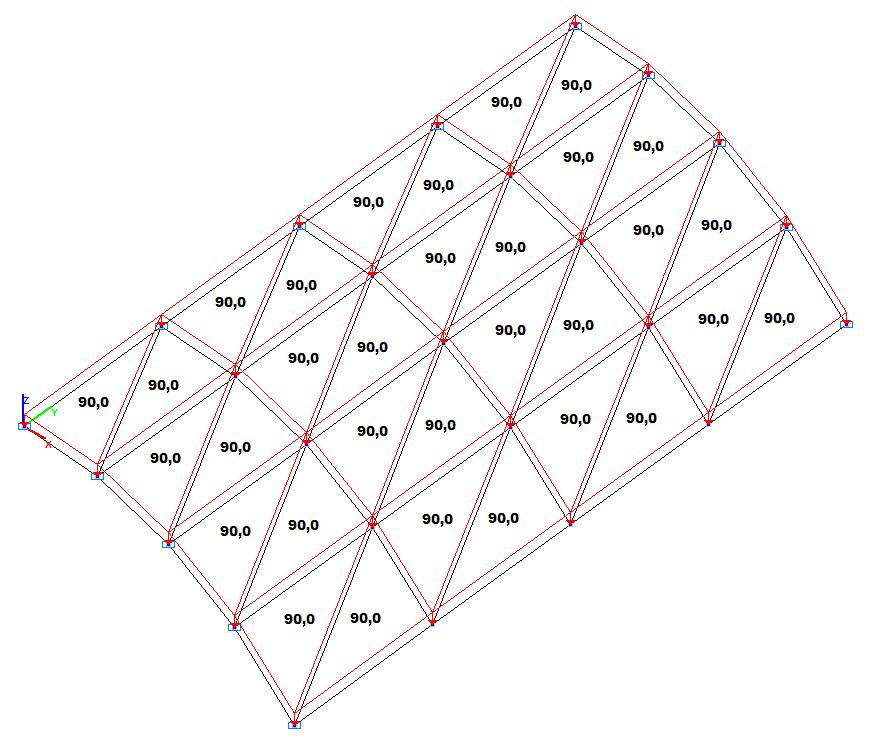

Model 1. Design model
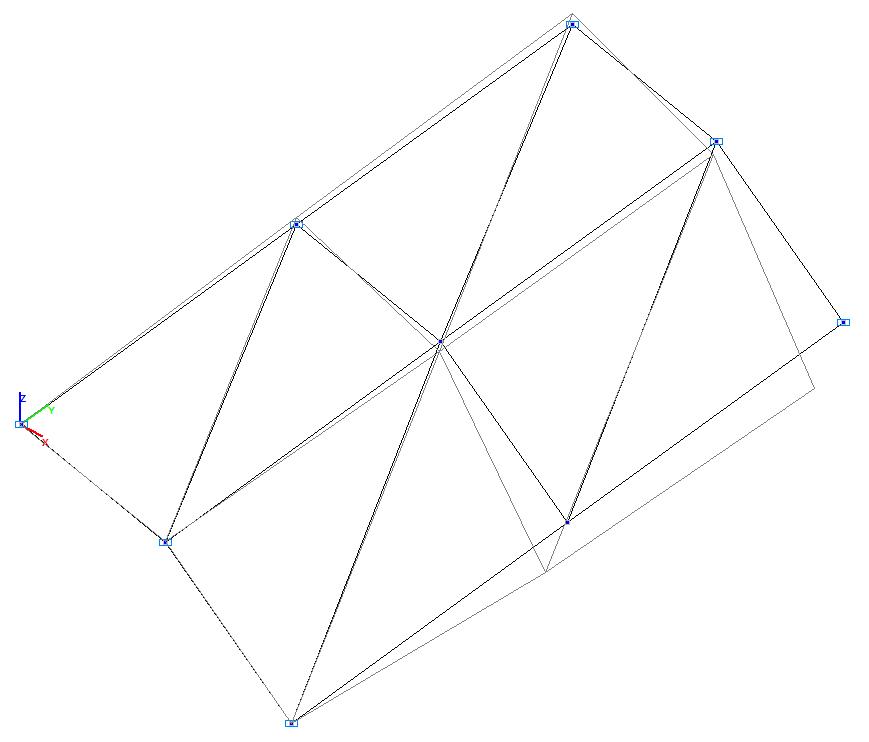
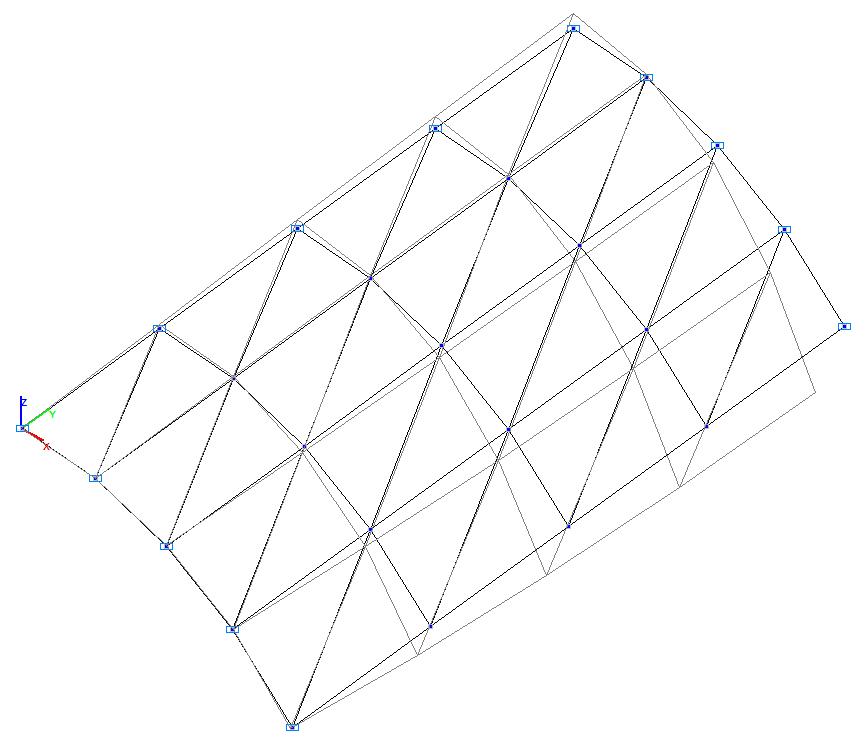
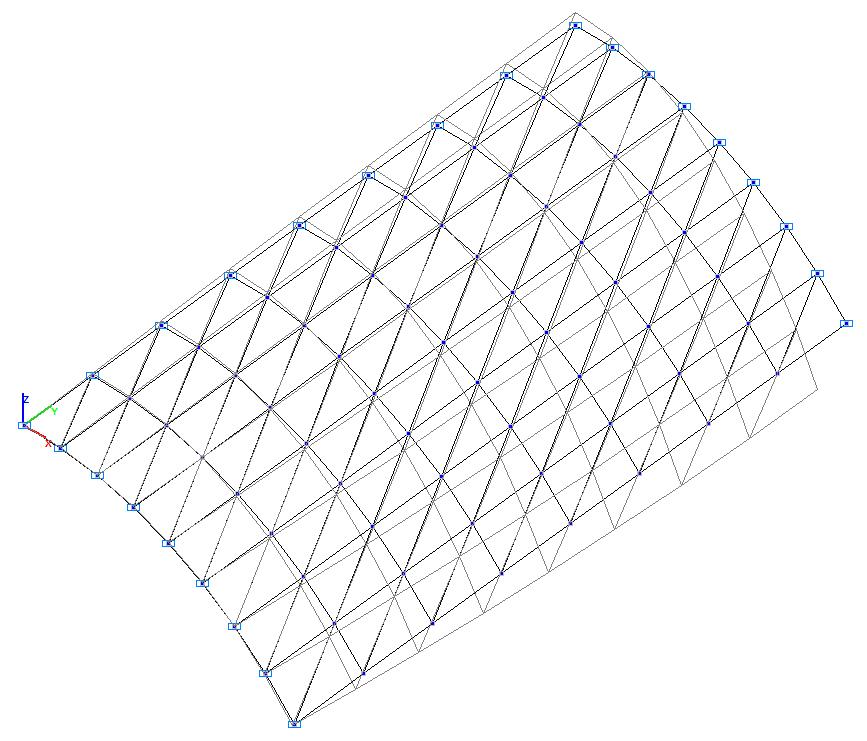
Model 1. Deformed model

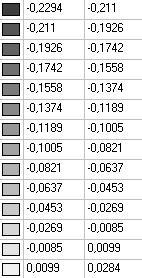

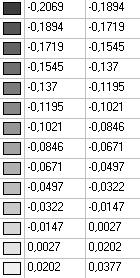

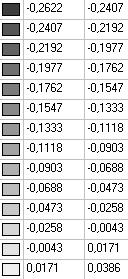
Model 1. Values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq (m)
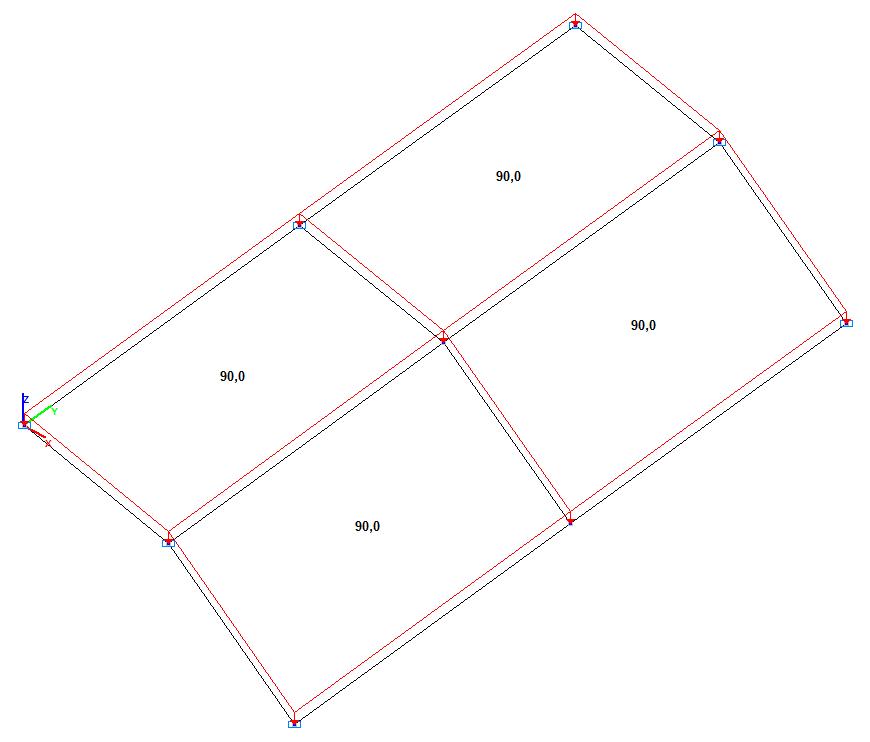
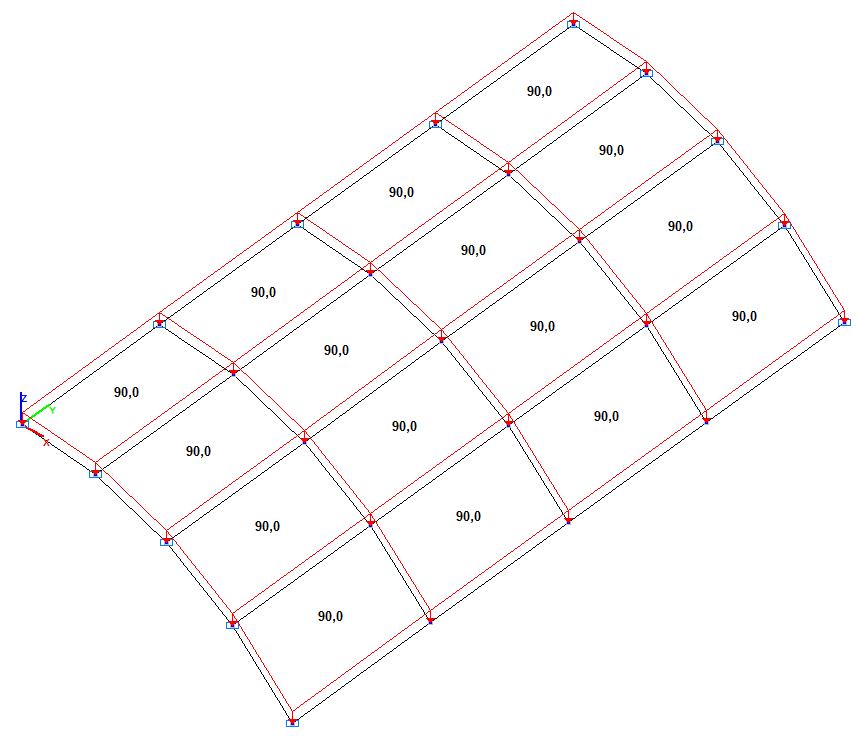

Model 2. Design model
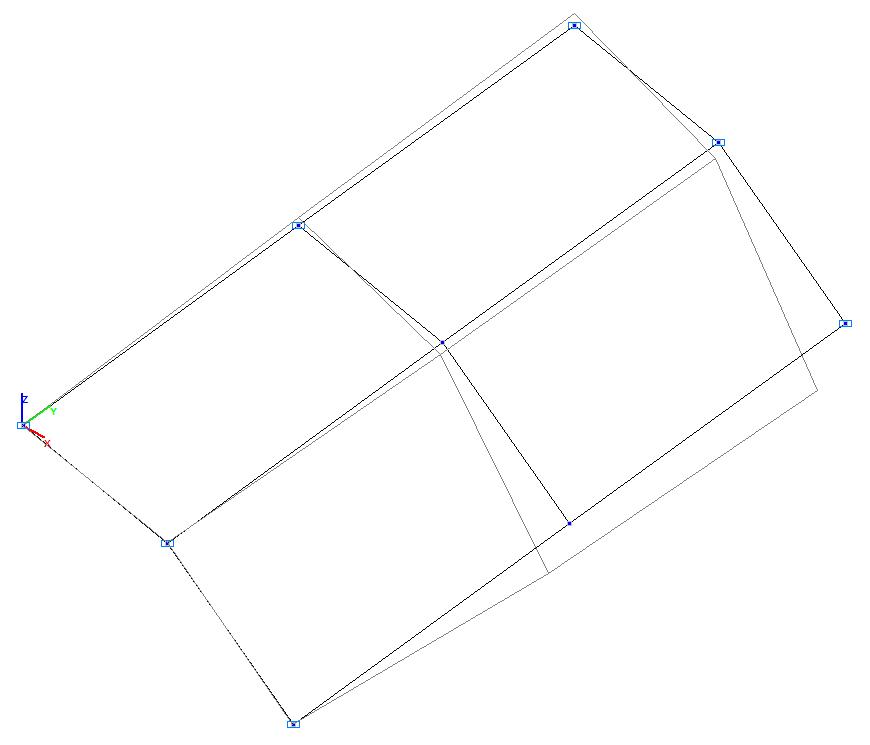
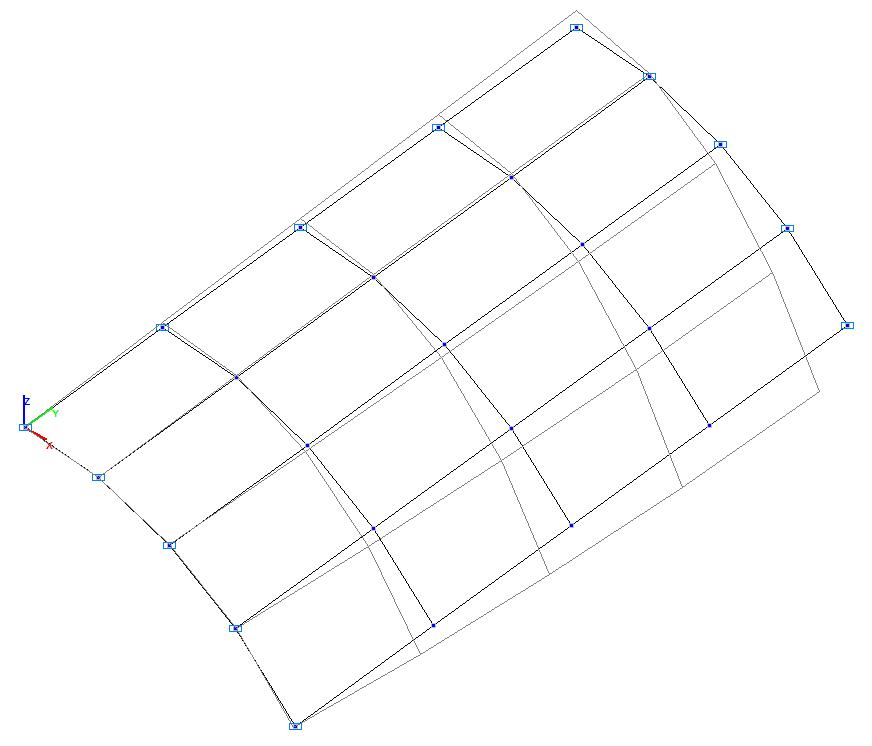
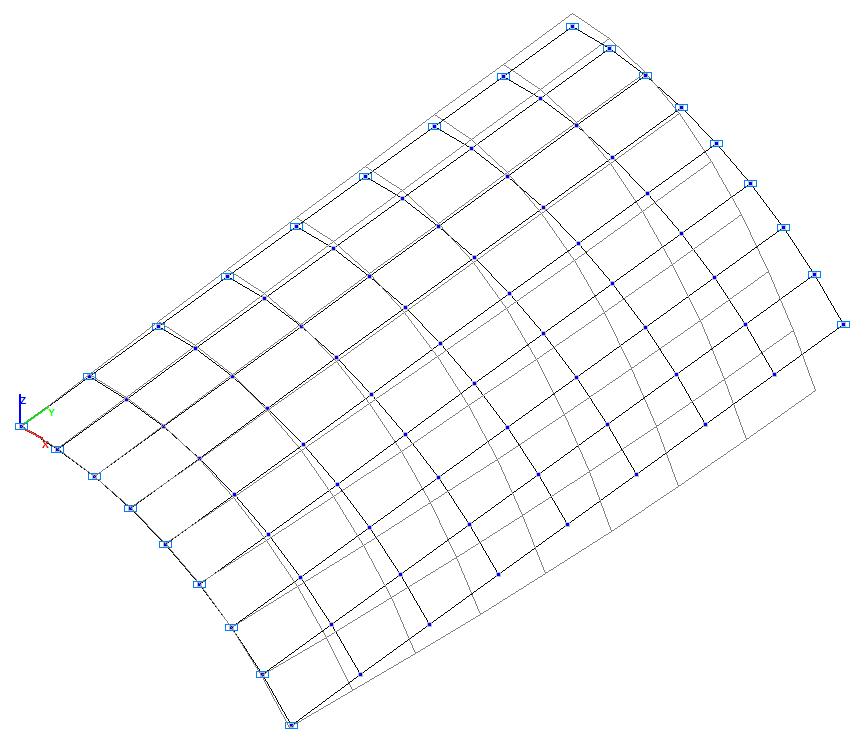
Model 2. Deformed model

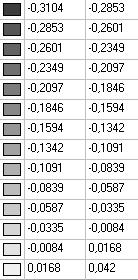

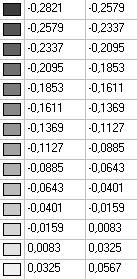


Model 2. Values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq (m)
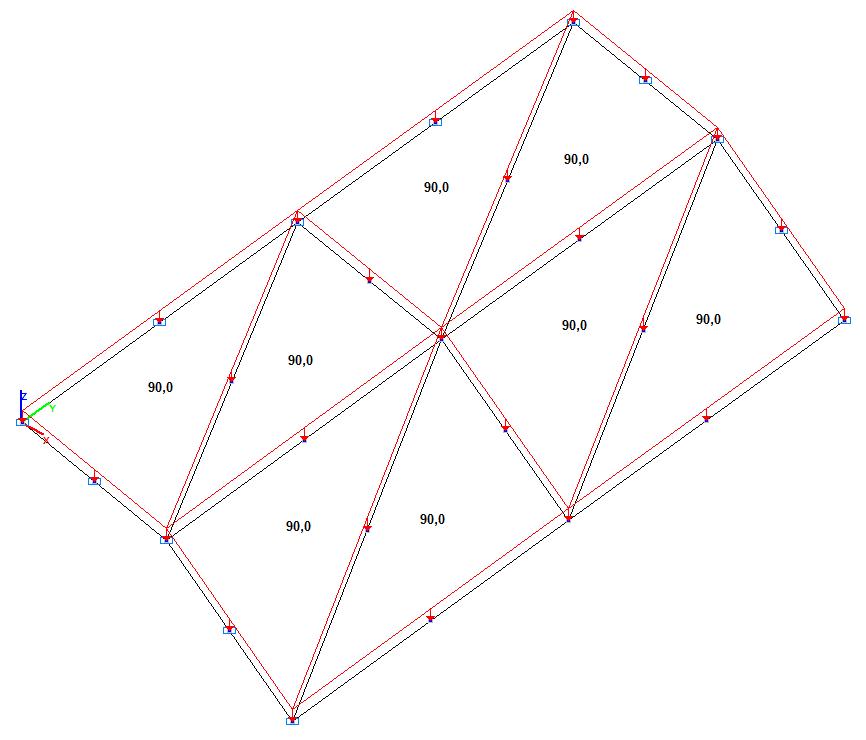
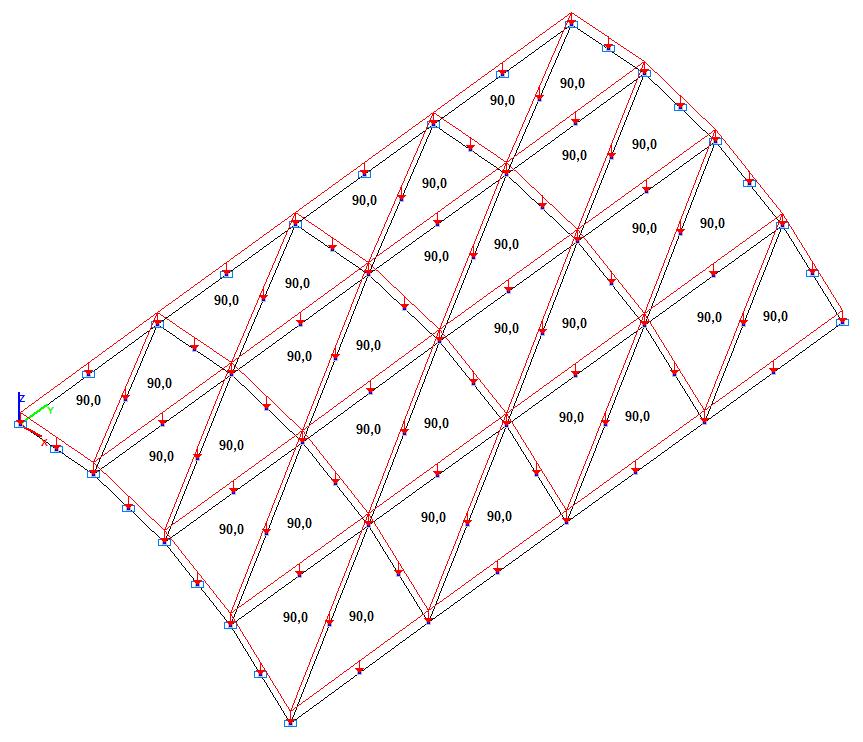

Model 3. Design model
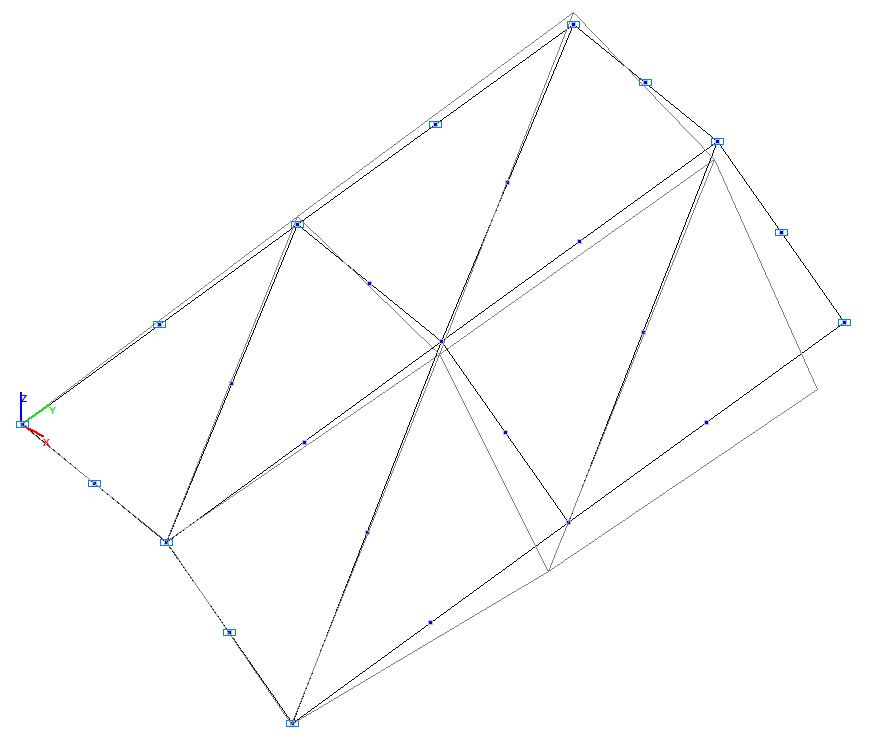
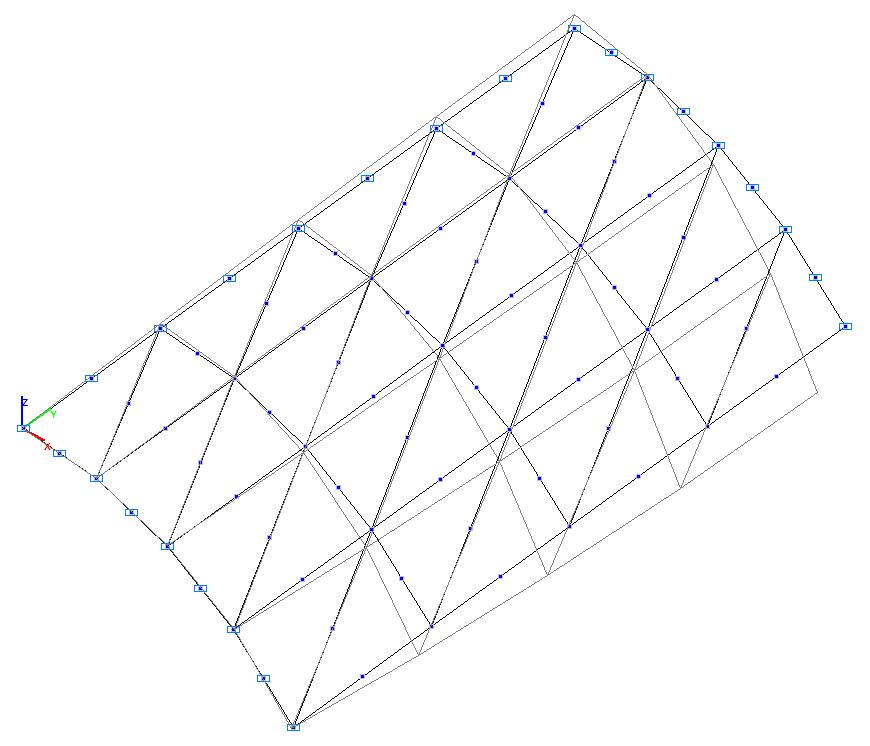
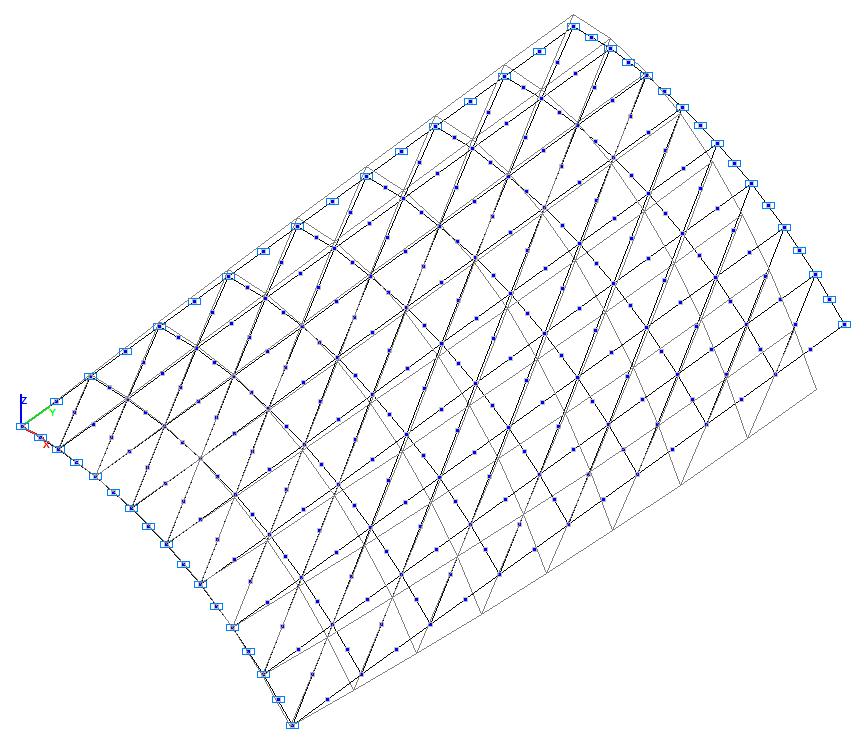
Model 3. Deformed model






Model 3. Values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq (m)
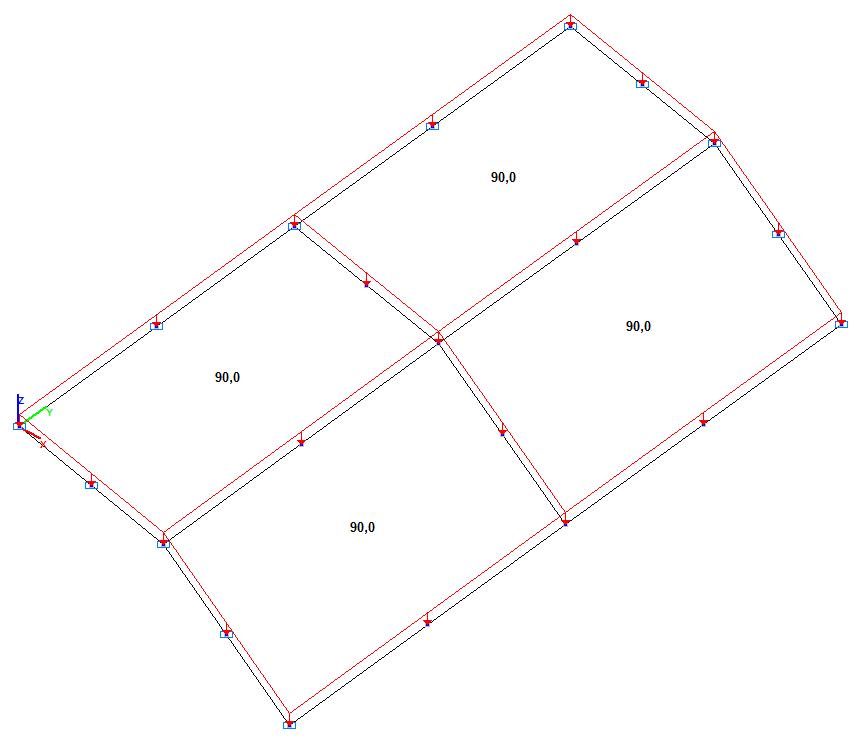
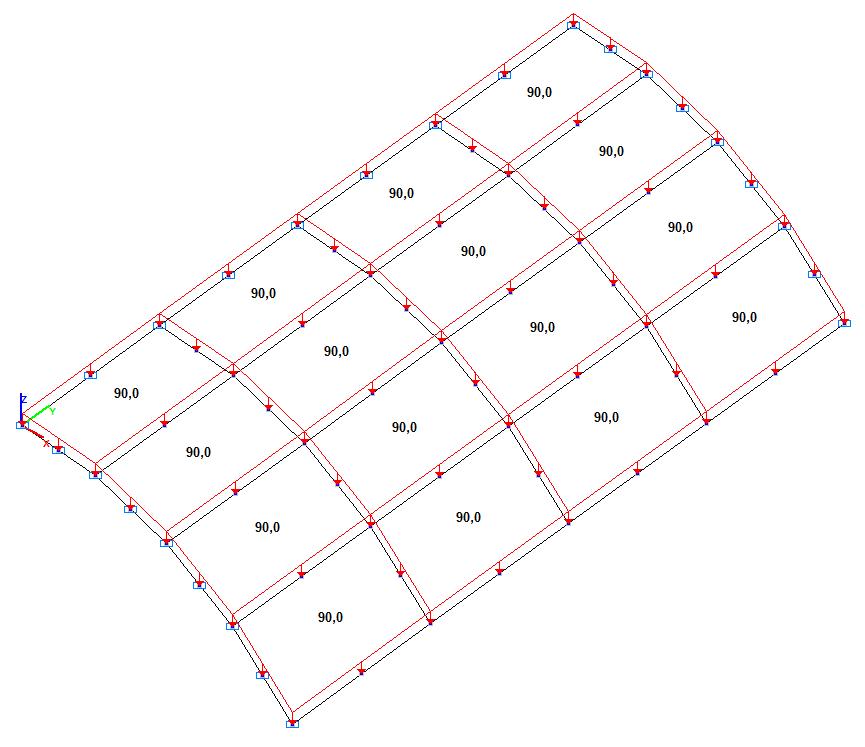

Model 4. Design mode
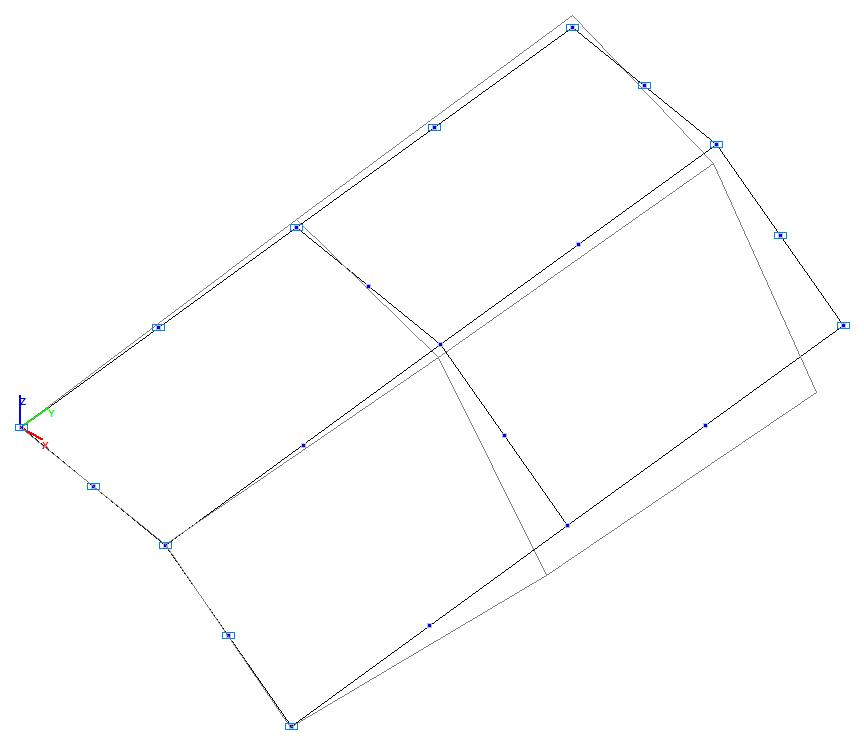
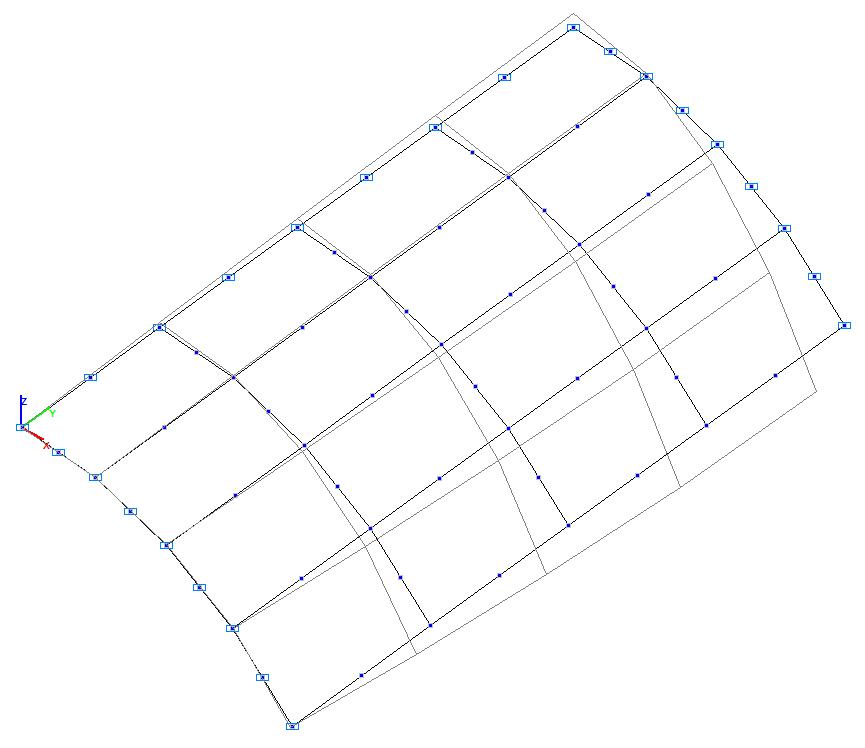
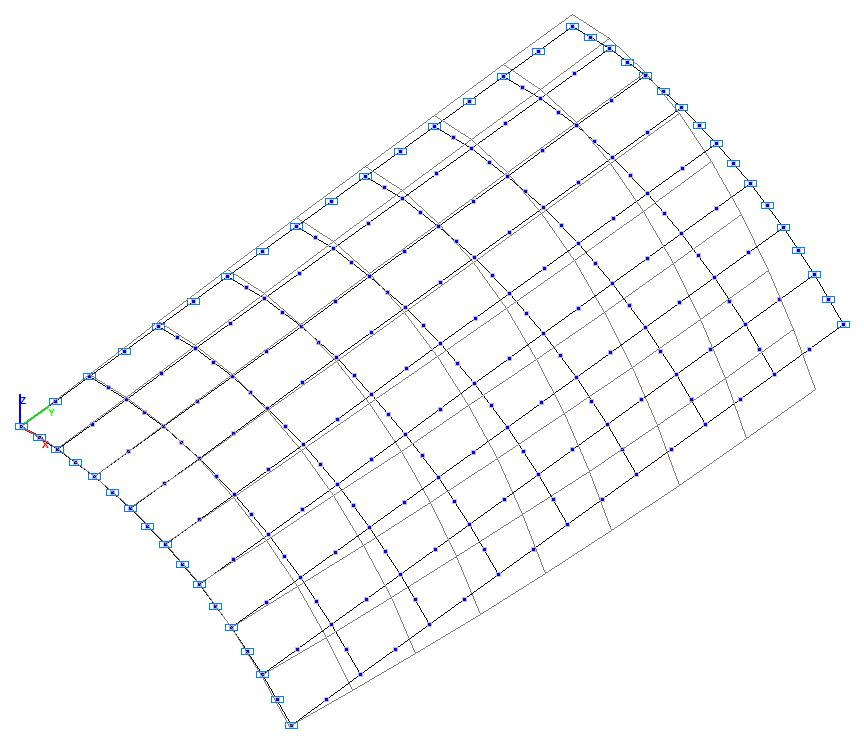
Model 4. Deformed model





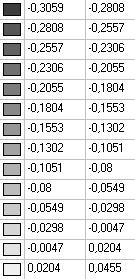
Model 4. Values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq (m)
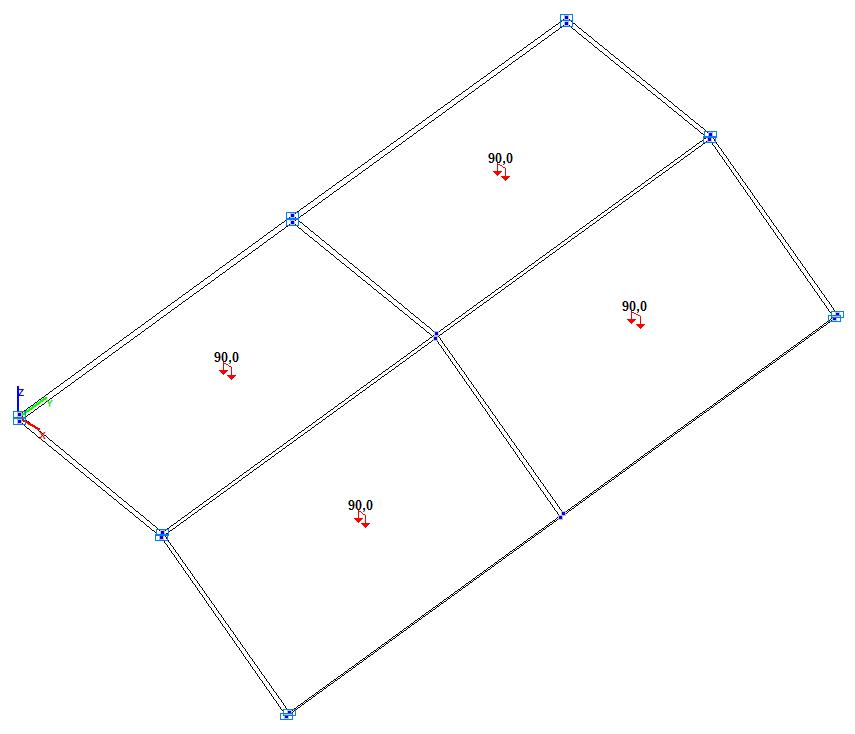
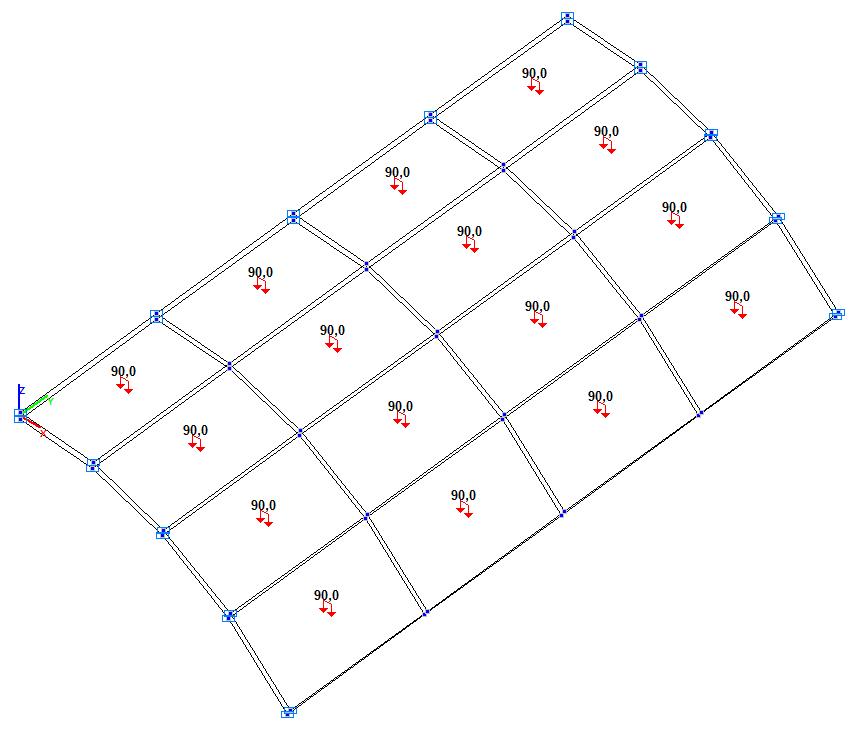
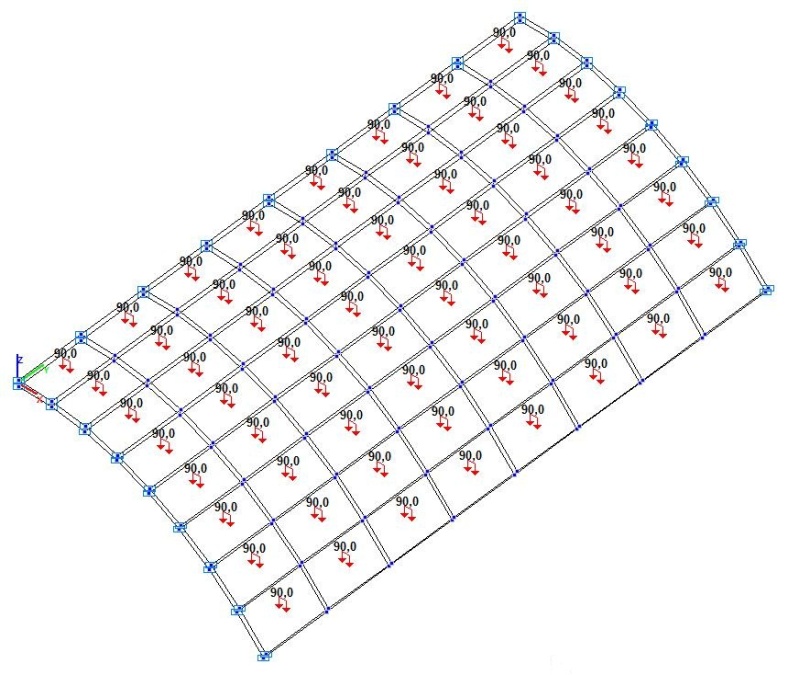




Model 5. Design model
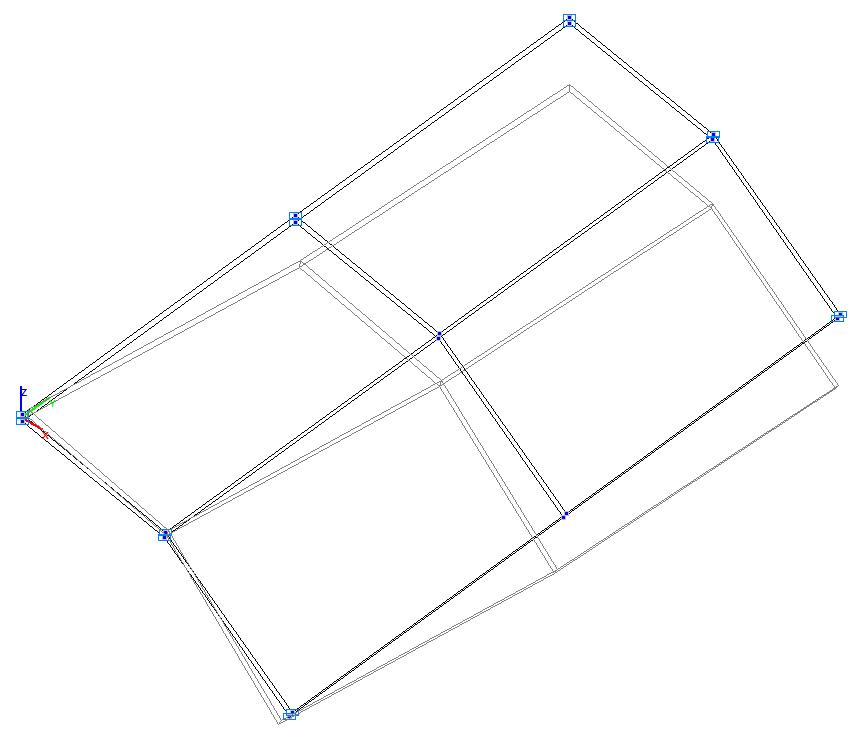
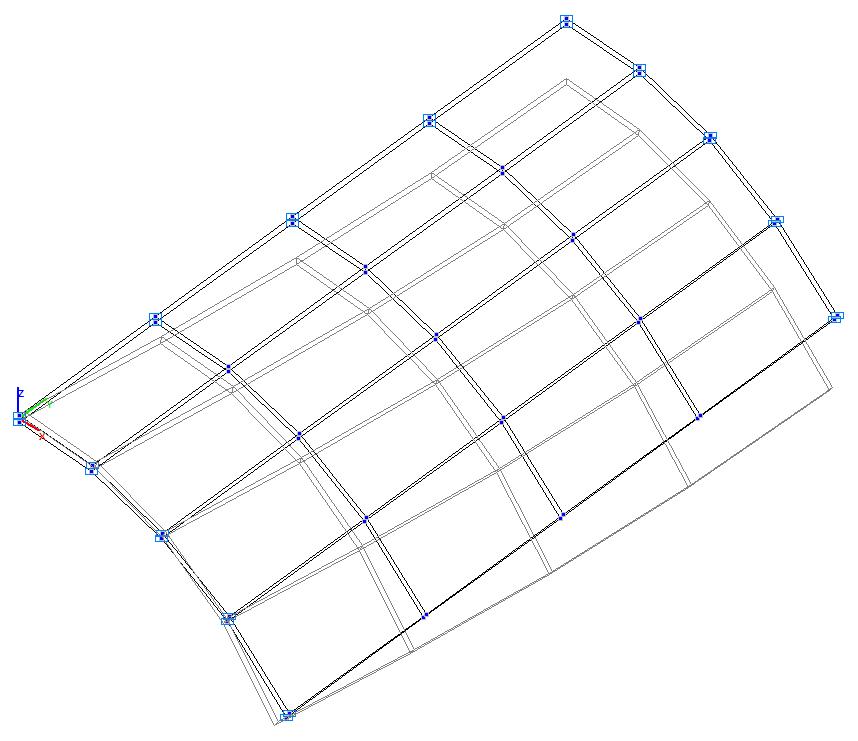
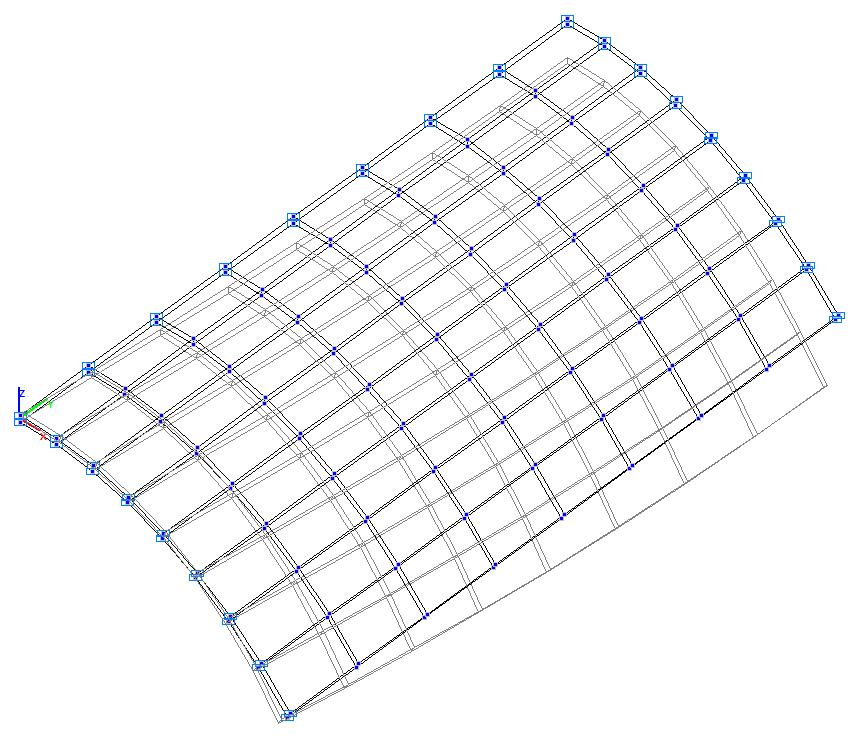




Model 5. Deformed model


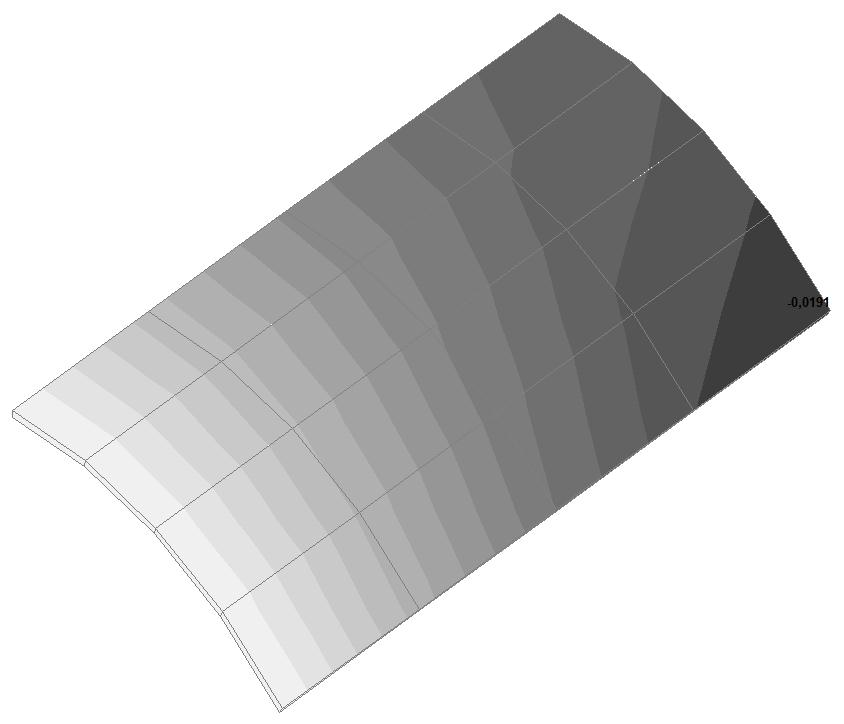
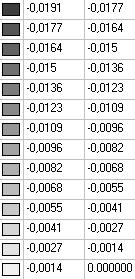








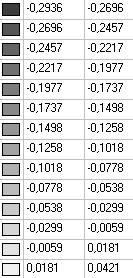
Model 5. Values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq (m)
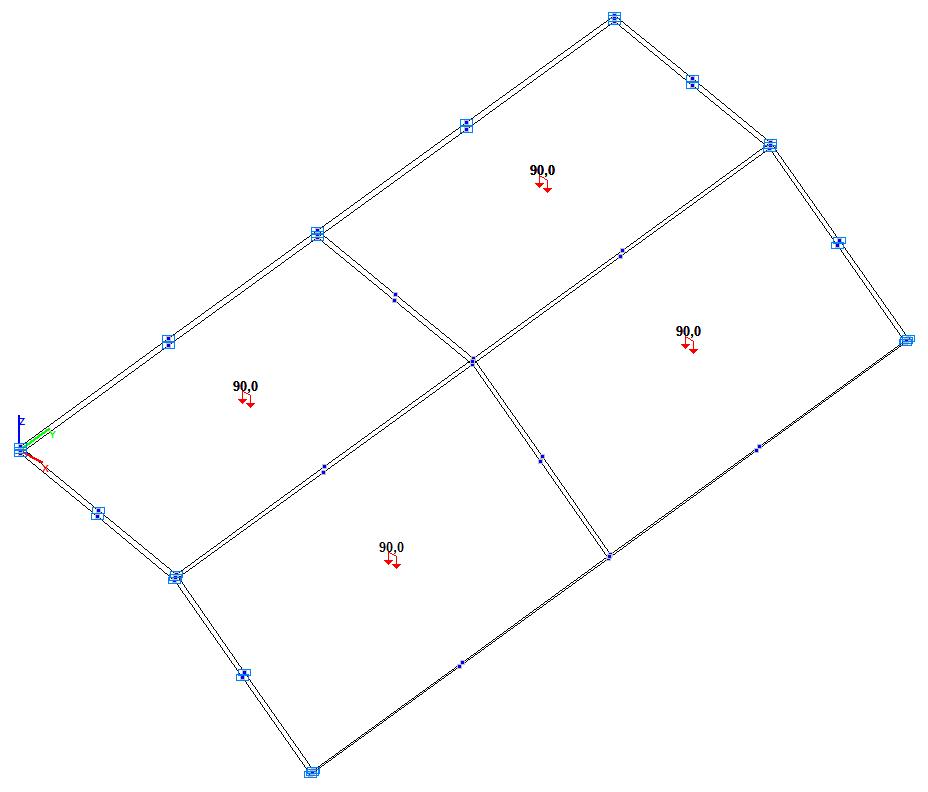
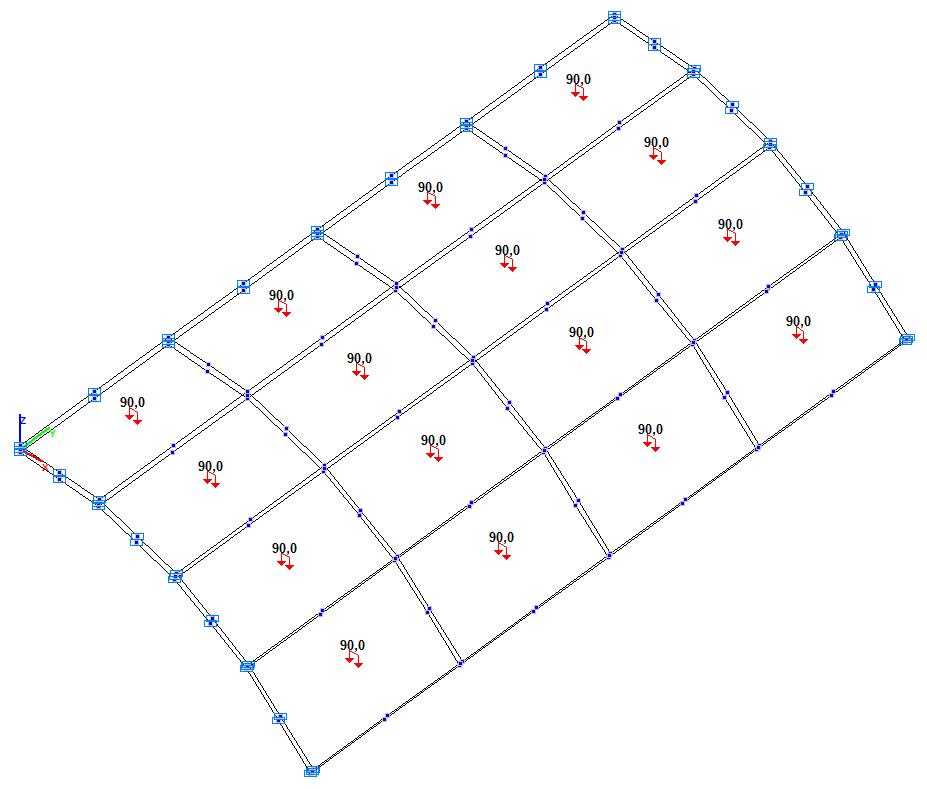
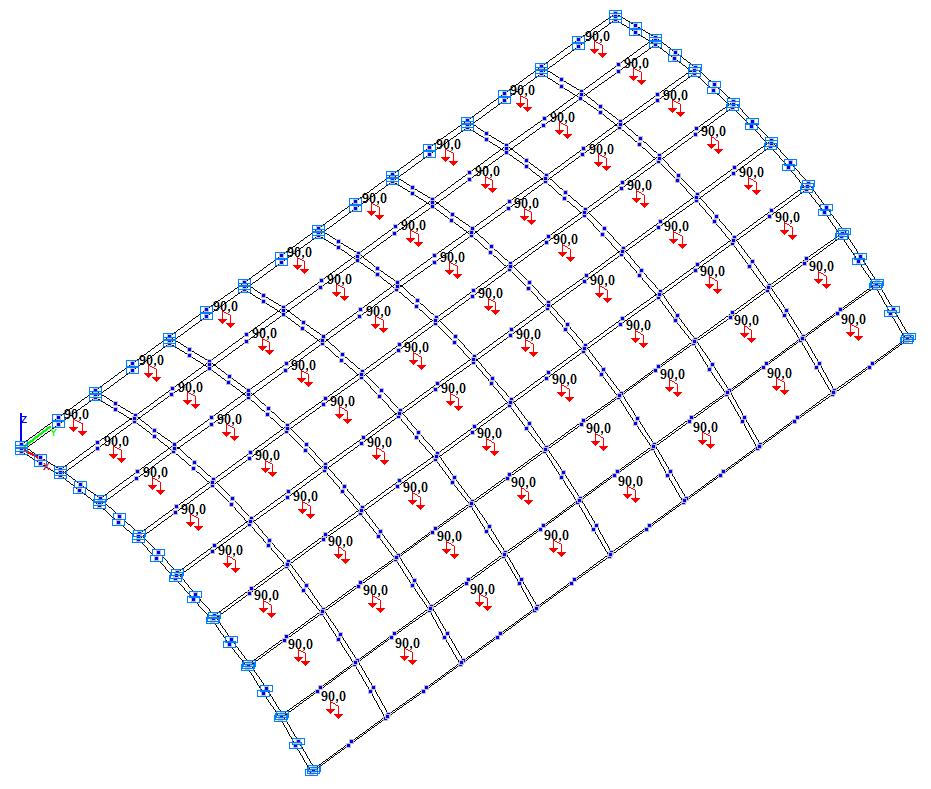




Model 6. Design model
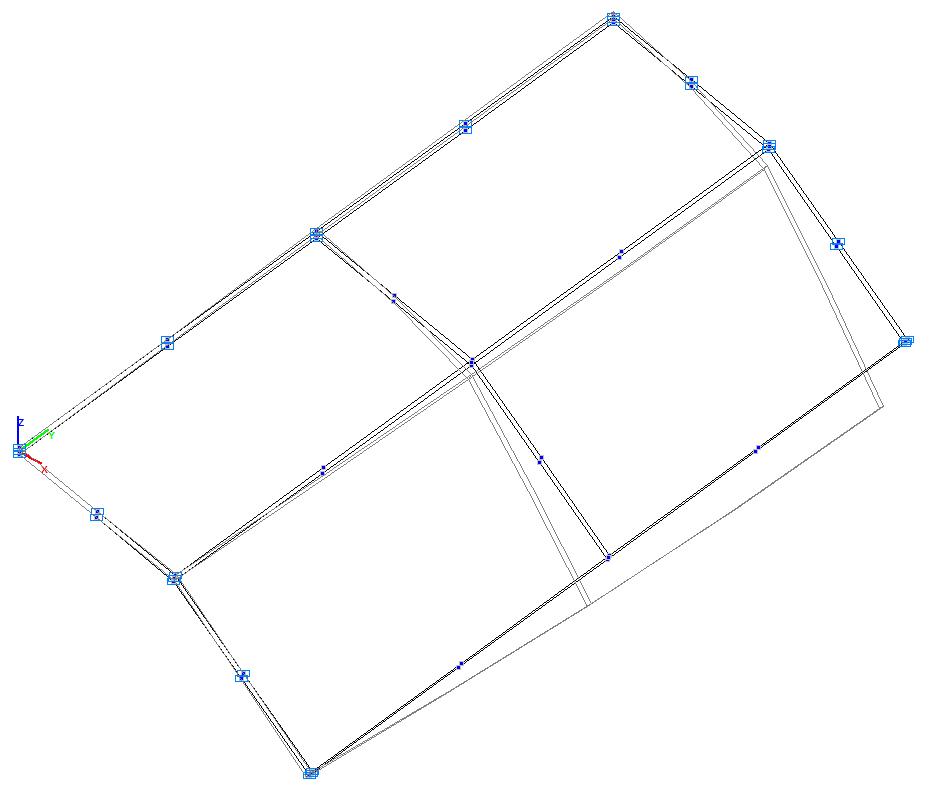
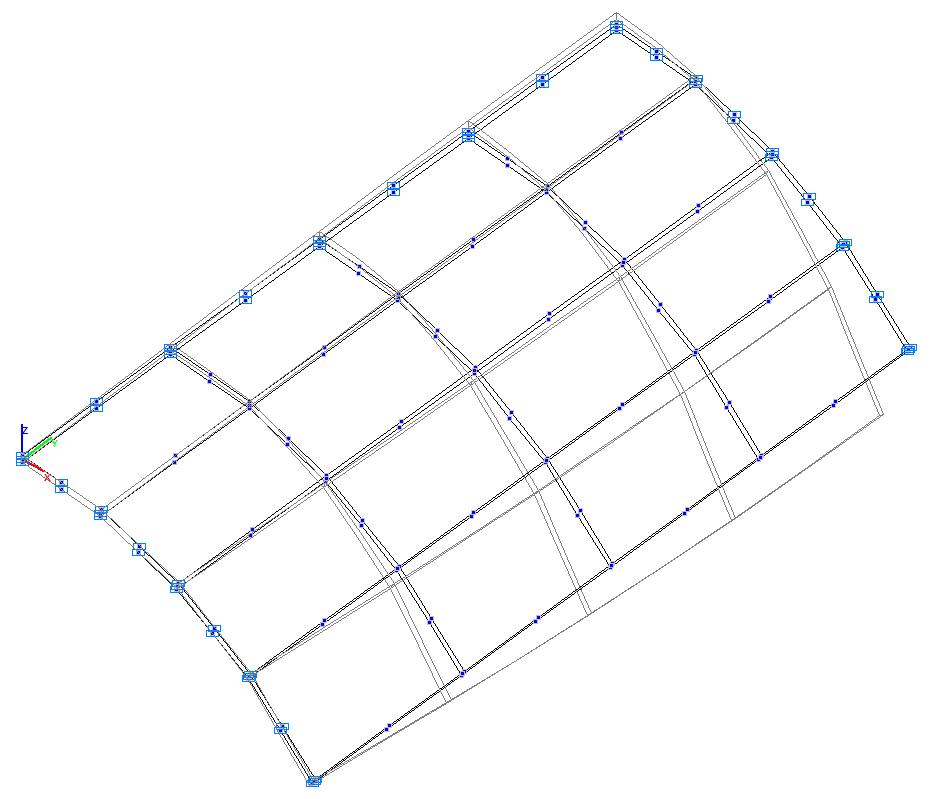
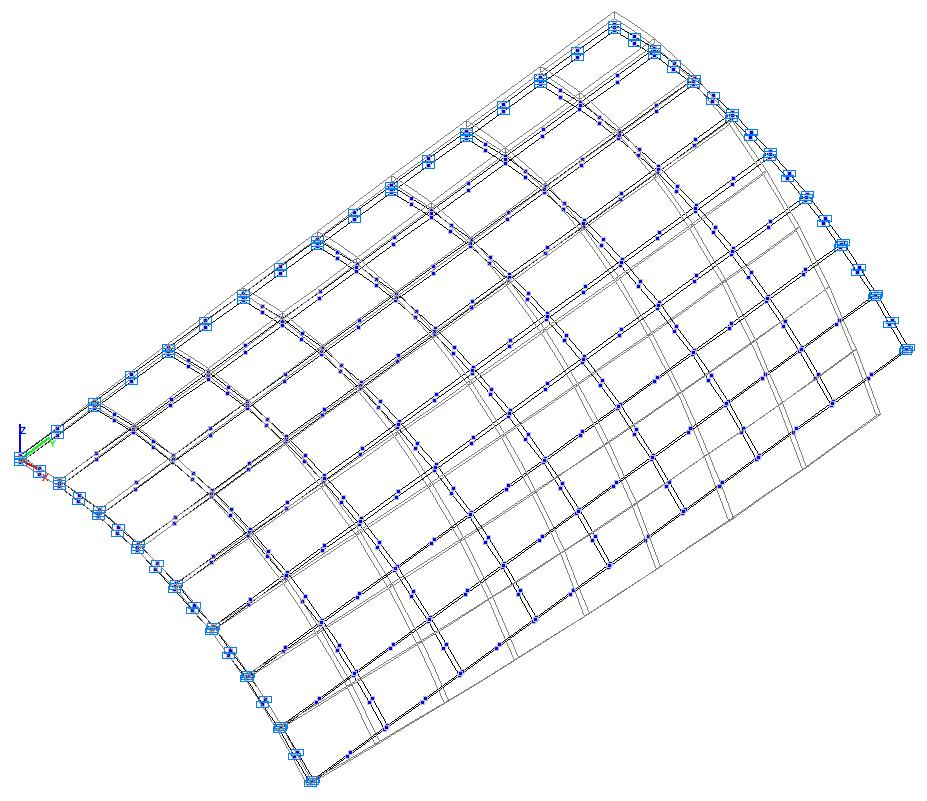




Model 6. Deformed model

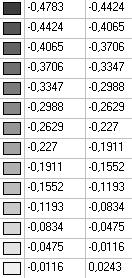

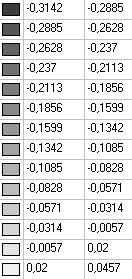

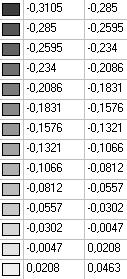








Model 6. Values of the transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq (m)
Comparison of solutions:
Transverse displacements in the middle of the free rectilinear edges of the open cylindrical shell wq from the transverse load q uniformly distributed over the entire area
|
Model |
Finite element mesh |
Theory |
SCAD |
Deviation, % |
|---|---|---|---|---|
|
1 (Member type 42) |
2x2 |
0.3086 |
0.2294 |
25.66 |
|
4x4 |
0.2069 |
32.95 |
||
|
8x8 |
0.2622 |
15.04 |
||
|
2 (Member type 44) |
2x2 |
0.3086 |
0.3104 |
0.58 |
|
4x4 |
0.2821 |
8.59 |
||
|
8x8 |
0.2941 |
4.70 |
||
|
3 (Member type 45) |
2x2 |
0.3086 |
0.3673 |
19.02 |
|
4x4 |
0.3107 |
0.68 |
||
|
8x8 |
0.3057 |
0.94 |
||
|
4 (Member type 50) |
2x2 |
0.3086 |
0.3693 |
19.67 |
|
4x4 |
0.3114 |
0.91 |
||
|
8x8 |
0.3059 |
0.87 |
||
|
5 (Member type 36) |
2x2 |
0.3086 |
0.0077 |
97.50 |
|
4x4 |
0.0191 |
93.81 |
||
|
8x8 |
0.0378 |
87.75 |
||
|
16x16 |
0.0806 |
73.88 |
||
|
32x32 |
0.1673 |
45.79 |
||
|
64x64 |
0.2532 |
17.95 |
||
|
128x128 |
0.2936 |
4.86 |
||
|
6 (Member type 37) |
2x2 |
0.3086 |
0.4783 |
54.99 |
|
4x4 |
0.3142 |
1.81 |
||
|
8x8 |
0.3105 |
0.62 |
||
|
16x16 |
0.3102 |
0.52 |
||
|
32x32 |
0.3104 |
0.58 |
||
|
64x64 |
0.3103 |
0.55 |
||
|
128x128 |
0.3104 |
0.58 |
