Doubly Clamped Beam Subjected to a Uniformly Distributed Load

Objective: Loading of a doubly clamped beam in one plane without taking into account the transverse shear deformations. The values of the maximum transverse displacement and the bending moments are checked.

Initial data file: 4_4.spr

Problem formulation: The doubly-clamped beam is subjected to a uniformly distributed load q. Determine the maximum transverse displacement w and bending moments М.

References: G.S. Pisarenko, A.P. Yakovlev, V.V. Matveev, Handbook on Strength of Materials. — Kiev: Naukova Dumka, 1988.

Initial data:

E = 2.0·1011 Pa	- elastic modulus,
μ = 0.3	- Poisson’s ratio,
l = 3 m	- beam length;
F = 14.2·10-4 m2	- cross-sectional area;
I   = 2.44·10-6 m4	- moment of inertia;
q = 10 kN/m	- load value.

 

Finite element model: Design model – plane frame, 10 bar elements of type 2, 11 nodes.

Results in SCAD

Bending moment diagram М (kN*m)    

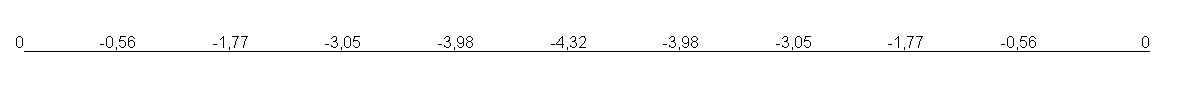
Values of transverse displacements  w (mm).

Comparison of solutions:

Parameter	Theory	SCAD	Deviations, %
Transverse displacement in the middle of the beam span, mm	-4.32	-4.32	0.00
Bending moment in the middle of the beam span, kN·m	3.75	3.75	0.00
Bending moment at the beam support, kN·m	-7.5	-7.5	0.00

Notes: In the analytical solution, the deflection at the center of the beam can be calculated according to the following formula ( “Handbook on Strength of Materials” p. 352):

\[ w=-\frac{q\cdot l^{4}}{384\cdot E\cdot I}; \]

Bending moments at the clamping are calculated according to the following formula:

\[ M=-\frac{q\cdot l^{2}}{12}; \]

Bending moment in the middle of the beam:

\[ M=\frac{q\cdot l^{2}}{24}. \]