Stability of an I-beam Simply Supported in and out of the Bending Plane Subjected to a Load Uniformly Distributed along the Longitudinal Axis of Its Upper Flange

Objective: Determination of the critical value of the load uniformly distributed along the longitudinal axis of the upper flange of an I-beam simply supported in and out of the bending plane corresponding to the moment of its buckling.

Initial data files:

File name	Description
Stability_Flanged_Beam_4_Bar.SPR Flanged_Beam.tns	Bar model Thin-walled beam cross-section
Stability_Flanged_Beam_4_Shell.SPR	Shell element model

Problem formulation: The I-beam simply supported in and out of the bending plane is subjected to the action of the load q, uniformly distributed along the longitudinal axis of its upper flange. Determine the critical value of the uniformly distributed load q_cr, corresponding to the moment of buckling of the simply supported beam.

References: A.S. Volmir. Stability of Deformable Systems, Moscow, Nauka, 1967, p.222;

Initial data:

L = 10.0 m	- length of the simply supported beam;
E = 3.0·107 kN/m2	- elastic modulus of the simply supported beam material;
ν = 0.2	- Poisson’s ratio;
b = bf = 0.5 m	- width of the flanges of the cross-section of the simply supported beam;
t = tf = 0.04 m	- thickness of the flanges of the cross-section of the simply supported beam;
hw = 1.0 m	- height of the web of the cross-section of the simply supported beam;
tw = 0.02 m	- thickness of the web of the cross-section of the simply supported beam;
q = 102 kN/m	- initial value of the transverse load uniformly distributed along the longitudinal axis of the upper flange of the beam.

 

Finite element model: Design model – general type system. Two design models are considered:

Bar model (B), 10 elements of type 5, the spacing of the finite element mesh along the longitudinal axis of the beam is 1.0 m. The reduced free torsional stiffness of the cross-section of the simply supported beam taking into account the warping effect is calculated according to the following formula: \( G\cdot I_{x\_{red}} =G\cdot I_{x} +\frac{\pi^{2}}{L^{2}}\cdot E\cdot I_{\omega } \). Boundary conditions are provided by imposing constraints on the nodes of the simply supported ends of the beam in the directions of the degrees of freedom X, Y, Z, UX. 11 vertical upward two-node elements of type 100 (3D rigid body) with the length h/2 are adjacent to the nodes of the beam. The action with the initial value of the uniformly distributed load q is specified in the free nodes of the elements of the rigid bodies (elevated application points) as concentrated forces P = q·1.0 = 10² kN (0.5·10² kN for end nodes). Number of nodes in the design model – 22;

Reissner-Mindlin shell element model (P), 2560 eight-node beam elements of type 150, the spacing of the finite element mesh along the longitudinal axis and along the height of the beam is 0.0625 m. Vertical stiffeners are arranged with a spacing of 1.0 m along the length in order to prevent the local buckling of the web and the flanges of the beam (h_w = 1.0 m; b_w = 0.5  m; t_w = 0.02 m; E = 3.0·10⁷ kN/m²; ν = 0.2), 3968 elements of type 150. Boundary conditions are provided by imposing constraints on the nodes of the ends of the beam lying on its longitudinal axis in the directions of the degrees of freedom X, Y, Z, and on all other nodes of the ends of the beam in the direction of the degree of freedom Y. The action with the initial value of the load q uniformly distributed along the line is specified on the upper sides of all elements of the beam web located under the upper flange of the beam. Number of nodes in the design model – 19793.

 

Results in SCAD

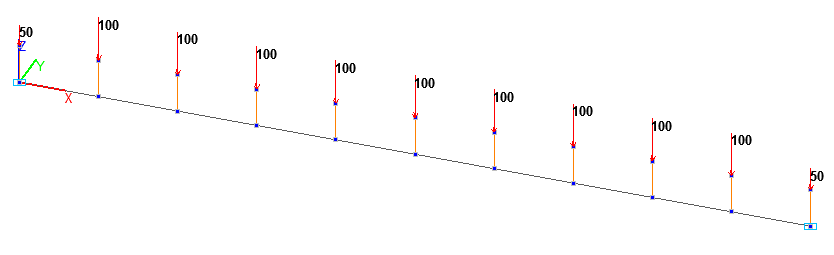
Design model. Bar model

 

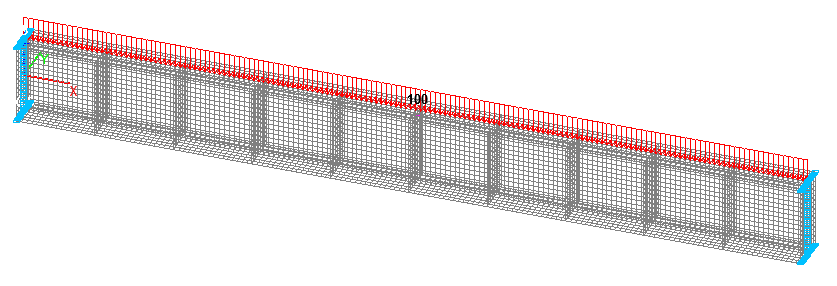
Design model. Reissner-Mindlin shell element model

 

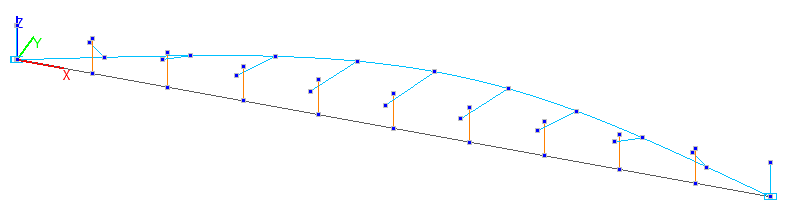
1-st buckling mode. Bar model

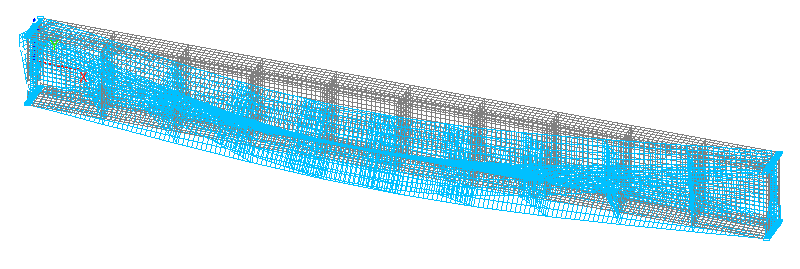
1-st buckling mode. Reissner-Mindlin shell element model

 

Comparison of solutions:

Critical value of the load qcr (kN/m), uniformly distributed along the longitudinal axis of the upper flange of the beam simply supported in and out of the bending plane

Design model	Theory	SCAD	Deviation, %
Bar	93	0,943201∙100= 94	1,54
Reissner-Mindlin shell element	93	0,949310∙100= 95	1,87

Notes: In the analytical solution the critical value of the transverse uniformly distributed load q_cr, corresponding to the moment of buckling of the simply supported beam can be determined according to the following formula:

\[ q=\frac{28,32\cdot \sqrt {E\cdot I_{z} \cdot G\cdot I_{x} } }{L^{3}}\cdot \chi \cdot k_{h} \quad \chi =\sqrt {1+\frac{\pi^{2}}{L^{2}}\cdot \frac{E\cdot I_{\omega } }{G\cdot I_{x} }} \quad G=\frac{E}{2\cdot \left( {1+\nu } \right)} \] \[ k_{h} =\sqrt {1+\frac{20,32}{\pi^{2}}\cdot \frac{E\cdot I_{\omega } }{G\cdot I_{x} \cdot L^{2}+\pi^{2}\cdot E\cdot I_{\omega } }} -\frac{4,50}{\pi }\cdot \sqrt {\frac{E\cdot I_{\omega } }{G\cdot I_{x} \cdot L^{2}+\pi^{2}\cdot E\cdot I_{\omega } }} \]

\( I_{z} =\frac{h_{w} \cdot t_{w}^{3}}{12}+2\cdot \frac{b_{f}^{3}\cdot t_{f} }{12} \)
 – minimum bending inertia moment (out of the moment plane);

\( I_{\omega } =\frac{h_{w}^{2}\cdot b_{f}^{3}\cdot t_{f} }{24} \) – sectorial constrained torsional inertia moment;

\( I_{x} =2\cdot k_{f} \cdot b_{f} \cdot t_{f}^{3}+k_{w} \cdot h_{w} \cdot t_{w}^{3} \) – free torsional inertia moment, where:

\[ k_{f} =\frac{1}{3}\cdot \left\{ {1-\frac{192}{\pi^{5}}\cdot \frac{t_{f} }{b_{f} }\cdot \sum\limits_{n=1}^\infty {\left[ {\sin^{2}\left( {\frac{n\cdot \pi }{2}} \right)\cdot \frac{1}{n^{5}}\cdot th\left( {\frac{n\cdot \pi \cdot h}{2\cdot b}} \right)} \right]} } \right\}, \] \[ k_{w} =\frac{1}{3}\cdot \left\{ {1-\frac{192}{\pi^{5}}\cdot \frac{t_{w} }{h_{w} }\cdot \sum\limits_{n=1}^\infty {\left[ {\sin^{2}\left( {\frac{n\cdot \pi }{2}} \right)\cdot \frac{1}{n^{5}}\cdot th\left( {\frac{n\cdot \pi \cdot h}{2\cdot b}} \right)} \right]} } \right\} \]