Two-Span Simply Supported Beam with an Intermediate Compliant Support Subjected to Concentrated Shear Forces Applied in the Middle of the Spans

Objective: Determination of the stress-strain state of a two-span simply supported beam with an intermediate compliant support subjected to concentrated shear forces applied in the middle of the spans.

Initial data file: SSLL03_v11.3.spr

Problem formulation: The two-span simply supported beam with an intermediate compliant support is subjected to concentrated shear forces F, applied in the middle of the spans (at the distance l from the end supports). Determine the vertical displacement Z and the vertical reaction N of the intermediate compliant support, and the bending moment M in the beam above the intermediate compliant support (point B).

References: C. Massonnet, Application des ordinateurs au calcul des structures, Paris, Eyrolles, 1968, p. 233.

Initial data:

E = 2.1·1011 Pa	- elastic modulus,
2·l = 6.0 m	- length of the beam span;
A = 0.4762·10-3 m2	- cross-sectional area;
I = 6,3·10-4 m4	- cross-sectional moment of inertia;
k = 2.1·1011 N/m	- stiffness of the intermediate compliant support
F = 4.2·104 N	- value of the concentrated shear forces.

 

Finite element model: Design model – plane frame, 4 bar elements of type 2. Boundary conditions are provided by imposing constraints in the directions of the degrees of freedom: X, Z – for the left support; Z – for the right support, and by imposing a constraint of finite rigidity in the direction of the degree of freedom Z – for the intermediate support (member type 51). Number of nodes in the design model – 5.

Results in SCAD

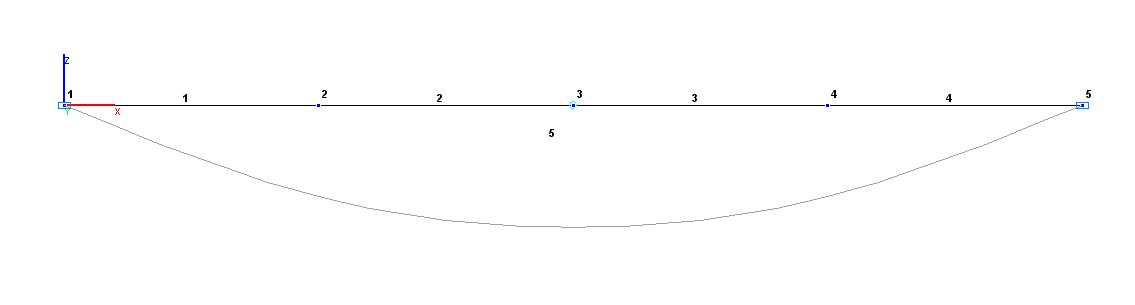
Design and deformed models

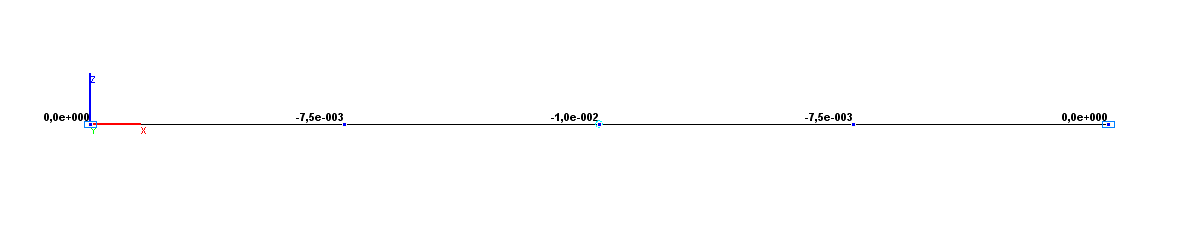
Values of vertical displacements Z (m)

Values of vertical support reactions N (N)

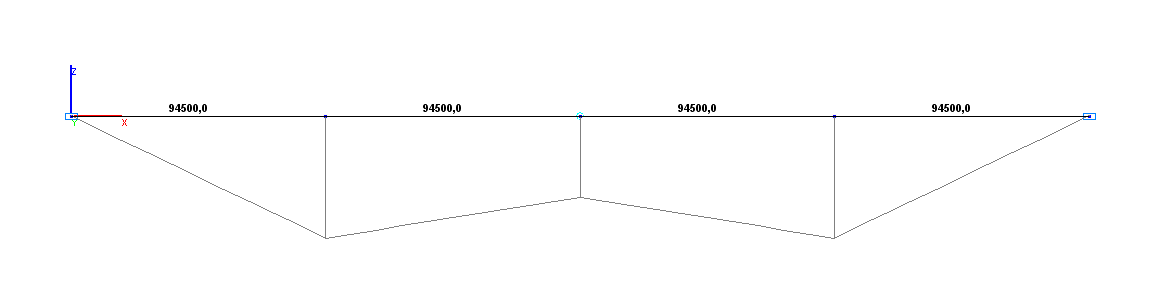
Bending moment diagram М (kN*m)

Comparison of solutions:

Parameter	Theory	SCAD	Deviations, %
Vertical displacement Z (point B), m	-1.0000·10-2	-1.0000·10-2	0.00
Vertical reaction H (point B), N	21000.0	21000.0	0.00
Bending moment M (point B), N·m	63000.0	63000.0	0.00