Strength and Stiffness Analysis of Secondary Beams for a Complex Stub Girder System
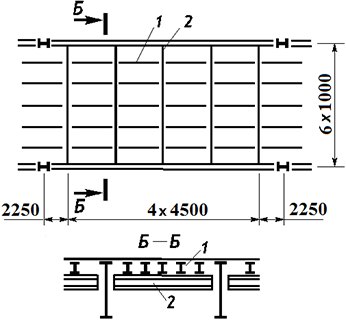
1 – stringer
2 – secondary beam
Objective: Check the mode for the beam analysis in the “Steel” postprocessor of SCAD.
Task: Select a rolled I-beam for the secondary beams with a span of 6 m in a complex stub girder system. The top chord of the secondary beams is restrained by the stringers arranged with a spacing of 1 m.
Source: Steel Structures: Student Handbook / [Kudishin U.I., Belenya E.I., Ignatieva V.S and others] - 13-th ed. rev. - M.: Publishing Center "Academy", 2011. p. 183.
Compliance with the codes: SNiP II-23-81*, SP 16.13330.2011, DBN B.2.6-163:2010.
Initial data file:
3.3 Beam_Example_3.3.spr;
report – 3.3 Beam_Example_3.3.doc
Initial data:
| а = 4,5 м | Spacing of secondary beams; |
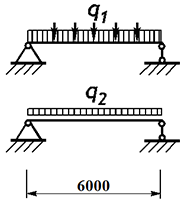
| qн = (0,77 + 27,3/102 + 20) kN/m2 × 4,5 m = 94,67 kN/m | Total characteristic load; |
| q1 = 1,05×(0,77 + 27,3/102) kN/m2 × 4,5 m = 4,9 kN/m | Design permanent load; |
| q2 = 1,2×20 kN/m2 × 4,5 m = 108 kN/m | Design temporary load; |
| Ry = 23 kN/cm2, | Steel grade C235; |
| l = 6,0 m | Beam span; |
| [ f ] = 1/250×6,0 m = 24 mm | Limit deflection; |
| γc = 1 | Service factor; |
| Wy = 2034,98 cm3 | Selected I-beam No.55 GOST 8239-89. |
| Iy = 55962 cm4. |
SCAD Results. STEEL Postprocessor:
[Element No. 1] Forces
|
N Max. 0 T Max. 0 T |
My Max. 0 T*m Max. 51,79 T*m |
Mz Max. 0 T*m Max. 0 T*m |
|
Mk Max. 0 T*m Max. 0 T*m |
Qz Max. 34,53 T Max. -34,53 T |
Qy Max. 0 T Max. 0 T |
|
|
Length of the bar 6 m |
|
[Element No. 1] Deflections
|
X |
Y |
Z
|
|
|
Length of the bar 6 m |
|
Analysis complies with SNiP II-23-81*
Structural member beam
Steel: C235
Member length 6 m
Limit slenderness for members in compression: 180
Limit slenderness for members in tension: 300
Service factor 1
Importance factor 1
Effective length factor XoZ -- 1
Effective length factor XoY -- 1
Length between out-of-plane restraints 0,01 m
Section
Profile: I-beam with sloped inner flange surfaces GOST 8239-89 55
|
Results |
Check |
Utilization factor |
|---|---|---|
|
Sec.5.12 |
Strength under action of bending moment My |
1,09 |
|
Sec.5.12,5.18 |
Strength under action of lateral force Qz |
0,49 |
|
Sec.5.24,5.25 |
Strength under combined action of longitudinal force and bending moments, no plasticity |
1,09 |
|
Sec.5.15 |
Stability of in-plane bending |
1,09 |
|
Sec.6.15,6.16 |
Limit slenderness in XoY plane |
0,59 |
|
Sec.6.15,6.16 |
Limit slenderness in XoZ plane |
0,09 |
Utilization factor 1,09 - Strength under action of bending moment My
Manual calculation:
1. Design bending moment acting in the beam span:
\[ M_{\max } =\frac{q_{\Sigma } l^{2}}{8}=\frac{\left( {4,9+108} \right)\cdot 6,0^{2}}{8}=508,05 \quad kNm. \]
2. Necessary beam section modulus assuming that the deformations of steel are elastic:
\[ W_{nes} =\frac{M_{\max } }{R_{y} }=\frac{508,05\cdot 100}{23}=2208,913 \quad cm^{3}. \].
3. Maximum deflection occurring in the middle of the beam span:
\[ f_{\max } =\frac{5}{384}\cdot \frac{q_{н} l^{4}}{EI_{y} }=\frac{5}{384}\cdot \frac{94,67\cdot 6,0^{4}}{2,06\cdot 10^{5}\cdot 10^{3}\cdot 55962\cdot 10^{-8}}=13,858 \quad mm. \].
4. Conditional limit slenderness of the compressed beam chord:
\[ \bar{{\lambda }}_{ub} =0,35+0,0032\frac{b_{f} }{t_{f} }+\left( {0,76-0,02\frac{b_{f} }{t_{f} }} \right)\frac{b_{f} }{h_{f} }=0,35+0,0032\frac{180}{16,5}+\left( {0,76-0,02\frac{180}{16,5}} \right)\frac{180}{533,5}=0,5677. \]
5. Conditional actual slenderness of the compressed beam chord:
\( \bar{{\lambda }}_{b} =\frac{l_{ef} }{b_{f} }\sqrt {\frac{R_{y} }{E}} =\frac{1000}{180}\sqrt {\frac{230}{2,06\cdot 10^{5}}} =0,1856<\bar{{\lambda }}_{ub} =0,5677 \) – the stability check is not required.
Comparison of solutions:
|
Factor |
Strength under action of lateral force |
Strength under action of bending moment |
Stability of in-plane bending under moment |
Maximum deflection |
|---|---|---|---|---|
|
Manual calculation |
not defined |
2208,913/2034,98 =1,085 |
check is not required |
13,858/24 = 0,577 |
|
SCAD |
0,488 |
1,085 |
1,085 |
16,53/1,1925/24 = 0,577 |
|
Deviation, % |
0,0 |
0,0 |
0,0 |
0,0 |
Comments:
- The check of tangential stresses was not performed in the manual calculation due to the absence of weakenings and a relatively large thickness of the beam webs.
- The check for the stability of in-plane bending of the beam was performed in the computer-aided calculation according to the codes at φb = 1,0.
- The check of the beam strength taking into account the development of the limited plastic deformations was not performed, because according to the codes this calculation is possible only when the beam web has stiffeners. In the initial data of the example a rolled beam without intermediate stiffeners was selected for the secondary beam.







