Strength and Stiffness Analysis of Main Beams of Complex Stub Girder Systems

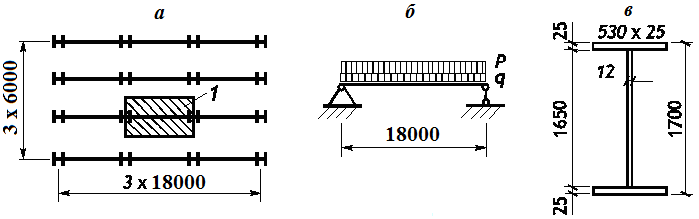
a – floor plan; b – design model of the main beam; c – beam section;
1 – load area

Objective: Check the mode for the beam analysis in the “Steel” postprocessor of SCAD

Task: Select a welded I-beam for the main beams with a span of 18 m in a normal stub girder system. The top chord of the main beams is restrained by the stringers arranged with a spacing of 1 m.

Source: Steel Structures: Student Handbook / [Kudishin U.I., Belenya E.I., Ignatieva V.S and others] - 13-th ed. rev. - M.: Publishing Center "Academy", 2011. p. 192.

Compliance with the codes: SNiP II-23-81*, SP 16.13330.2011, DBN B.2.6-163:2010.

Initial data file:

3.4 Beam_Example_3.4.spr;
report – 3.4 Beam_Example_3.4.doc

Initial data:

а = 6 м	Spacing of main beams;
g₁ = 1,16 kN/m²	Weight of the floor plate and stringers;
p = 20 kN/m²	Temporary (live) load;
q_н = 127,099 kN/m	Total characteristic load on the beam;
q₁ = 1,051,16 kN/m² 6 m*1,02 = 7,454 kN/m	Design permanent load (coefficient 1,02 allows for the self-weight of the main beam);
q₂ = 1,220 kN/m² 6 m = 144,0 kN/m	Design live load;
l = 18 m	Main beam span;
R_y= 23 kN/cm² R_s = 0,58*23=13,34 kN/cm²	Steel grade C255 with thickness t>20 mm;
[ f ] = l/400 = 45 mm	Limit deflection;
b_p×t_p = 530×20 mm	Section of the bearing stiffener;
k_p = 6 mm	Fillet weld leg in a welded connection between a bearing stiffener and a beam;
γ_c = 1	Service factor;
W_y = 27153,85 cm³	Geometric properties for a welded I-section with flanges 530×25 mm
I_y = 2308077,083 cm⁴	and a web 1650×12 mm;
S_y = 15180,625 cm³.

SCAD Results. STEEL Postprocessor:

[Element No 3] Forces

Max. 0 T
Snap 0 m

M_y

Max. 625,27 T*m
Snap 4,5 m

M_z

Max. 0 T*m
Snap 0 m

M_k

Max. 0 T*m
Snap 0 m

Q_z

Max. 69,47 T
Snap 0 m

Max. 0 T
Snap 4,5 m

Q_y

Max. 0 T
Snap 0 m

Length of the bar 4,5 m
Length of the flexible part 4,5 m
Loading L1 - "1"

[Element No. 3] Deflections

Max. -43,54 mm
Snap 4,5 m

Length of the bar 4,5 m
Length of the flexible part 4,5 m
Loading L1 - "1"

Analysis complies with SNiP II-23-81*
Structural member main beam

Steel: C255

Member length 18 m
Limit slenderness for members in compression: 180
Limit slenderness for members in tension: 300
Service factor 1
Importance factor 1
Effective length factor XoZ -- 1
Effective length factor XoY -- 1
Length between out-of-plane restraints 1 m

Section

Results	Check	Utilization factor
Sec.5.12	Strength under action of bending moment My	0,98
Sec.5.12,5.18	Strength under action of lateral force Qz	0,56
Sec.5.24,5.25	Strength under combined action of longitudinal force and bending moments, no plasticity	0,98
Sec.5.15	Stability of in-plane bending	0,98
Sec.6.15,6.16	Limit slenderness in XoY plane	0,52
Sec.6.15,6.16	Limit slenderness in XoZ plane	0,08

Utilization factor 0,98 - Strength under action of bending moment M_y

Manual calculation (SNiP II-23-81*)

1. Maximum bending moment and shear force acting in the design sections of the beam:

\[ M_{\max } =\frac{q_{\Sigma } l^{2}}{8}=\frac{\left( {7,454+144} \right)\cdot 18,0^{2}}{8}=6133,887 \quad kNm. \] \[ Q_{\max } =\frac{q_{\Sigma } l}{2}=\frac{\left( {7,454+144} \right)\cdot 18,0}{2}=1363,086 \quad kN. \]

2. Necessary beam section modulus:

\[ W_{nes} =\frac{M_{\max } }{R_{y} \gamma_{c} }=\frac{6133,887\cdot 100}{23}=26669,074 \quad cm^{3}. \]

3. Maximum tangential stresses in the support section of the beam:

\[ \tau_{\max } =\frac{Q_{\max } S_{y} }{I_{y} t_{w} }=\frac{1363,086\cdot 15180,625}{2308077,083\cdot 1,2}=7,471 \quad kN/cm^{2}. \]

4. Maximum deflection occurring in the middle of the beam span:

\[ f_{\max } =\frac{5}{384}\cdot \frac{q_{н} l^{4}}{EI_{y} }=\frac{5}{384}\cdot \frac{127,099\cdot 18,0^{4}}{2,06\cdot 10^{5}\cdot 10^{3}\cdot 2308077,083\cdot 10^{-8}}=36,539 \quad mm. \]

5. Conditional limit slenderness of the compressed beam chord:

\[ \bar{{\lambda }}_{ub} =0,35+0,0032\frac{b_{f} }{t_{f} }+\left( {0,76-0,02\frac{b_{f} }{t_{f} }} \right)\frac{b_{f} }{h_{f} }=0,35+0,0032\frac{530}{25}+\left( {0,76-0,02\frac{530}{25}} \right)\frac{530}{1675}=0,524. \]

6. Conditional actual slenderness of the compressed beam chord:

\( \bar{{\lambda }}_{b} =\frac{l_{ef} }{b_{f} }\sqrt {\frac{R_{y} }{E}} =\frac{1000}{530}\sqrt {\frac{230}{2,06\cdot 10^{5}}} =0,063<\bar{{\lambda }}_{ub} =0,524 \) – the stability check is not required.

Comparison of solutions:

Factor	Manual calculation	SCAD
Strength under action of lateral force	7,471/13,34 = 0,56	0,56
Strength under action of bending moment	26669,074/27153,85=0,982	0,982
Stability of in-plane bending under moment	–	0,982
Maximum deflection	36,539/45 = 0,812	43,54/1,1916/45= 0,812

Comments:

The check for the stability of in-plane bending of the beam was performed in the computer-aided calculation according to the codes at φ_b = 1,0.